1. 개념
암호화와 복호화에 하나의 같은 키를 사용하는 암호 시스템
- 대칭키, 비밀키, 단일키, 관용암호 등과 같은 이름으로 불리기도 한다.
-
: 암호화
- : 평문
- : 키
- : 암호문
-
: 복호화
- : 평문
- : 키
- : 암호문
가) 고려해야할 점
- 암호화, 복호화 시 같은 키를 사용하기 때문에
키를 무사히 전달할 수 있는 안전한 채널이 필요하다.
나) 대칭키 암호 종류
전통적
- Rail fence
- Columnar
- Shift
블록 암호 ( Block Cypher )
- AES
- TDEA
- DES
- ARIA
- SEED
스트림 암호 ( Stream Cypher )
- RC4
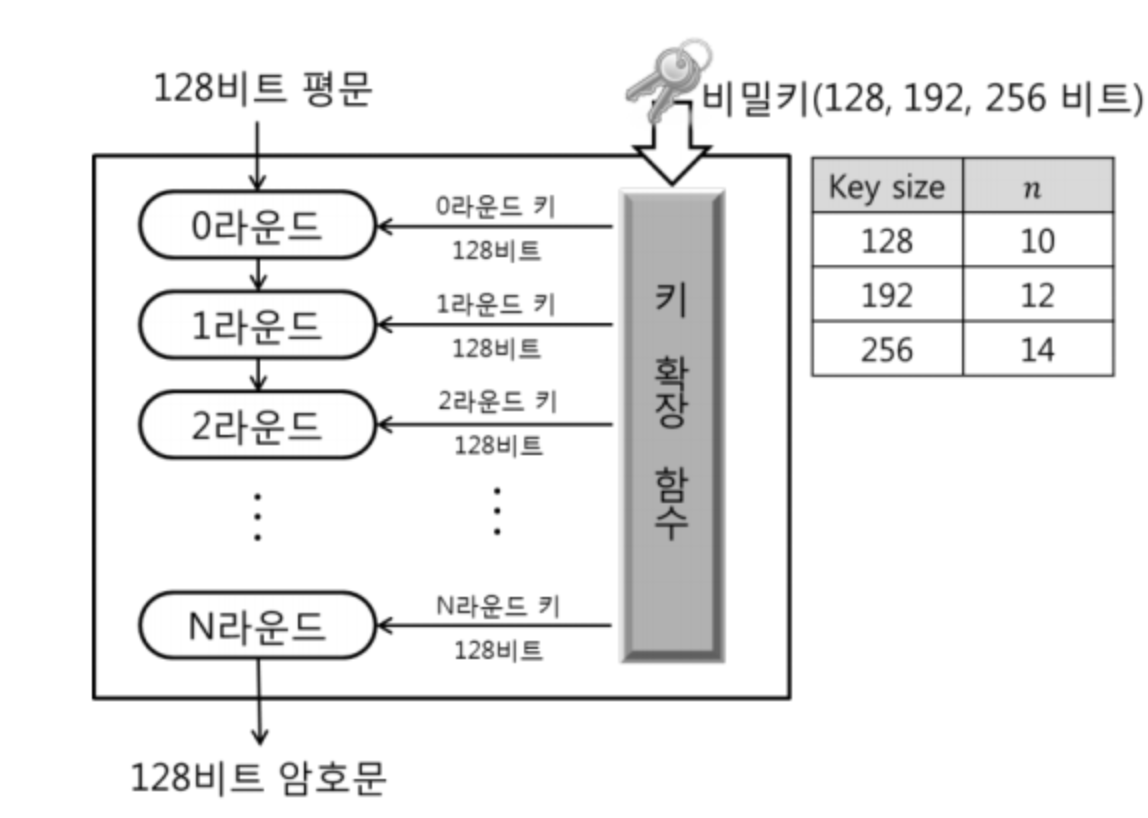
2. AES
- Advanced Encryption Standard
미국 NIST에서 2001년 공표한 표준 대칭키 암호 시스템
- AES 선정 과정
- 1997년: 공모 개시
- 128 bits 블록, 키 크기 128, 192, 256 bits, 로열티 프리
- 1998년: 제출된 21개 암호 시스템 중 15개 선정
- 1999년 5개 후보 선정
- MARS, RC6, Rijndael....
- 2000년 Rijndael을 AES로 선정
- 2001년: AES를 표준으로 공식 발표
가) 입출력
- 평문 블록 크기
- 128 bits
- 키 크기
- 128 bits, 192 bits, 256 bits 중 한 가지 선택
- 암호문 블록 크기
- 128 bits
나) 암호화
구성
- 초기화 함수
- N-1개의 라운드
- 1개의 라운드
- 종료화 함수
- 키 생성
- 각 라운드 마다 키를 생성하는 목적
암호화
Byte 단위의 연산
다) 초기화
-
16 bytes (=128 bits)의 입력 데이터를 행렬인 state로 변환
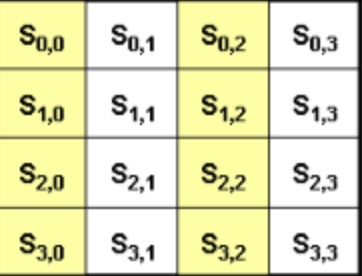
- 1 byte
-
AddRoundKey 작업 수행
- state에 Round Key를 XOR 연산을 진행한다.
- XOR: 11001110
- XOR을 다 진행하고 다면 행렬이 나오게 된다.
라) 라운드
-
SubBytes 연산
- 비선형성을 갖는 S-box를 state에 적용하여 바이트 단위 치환
- S-box
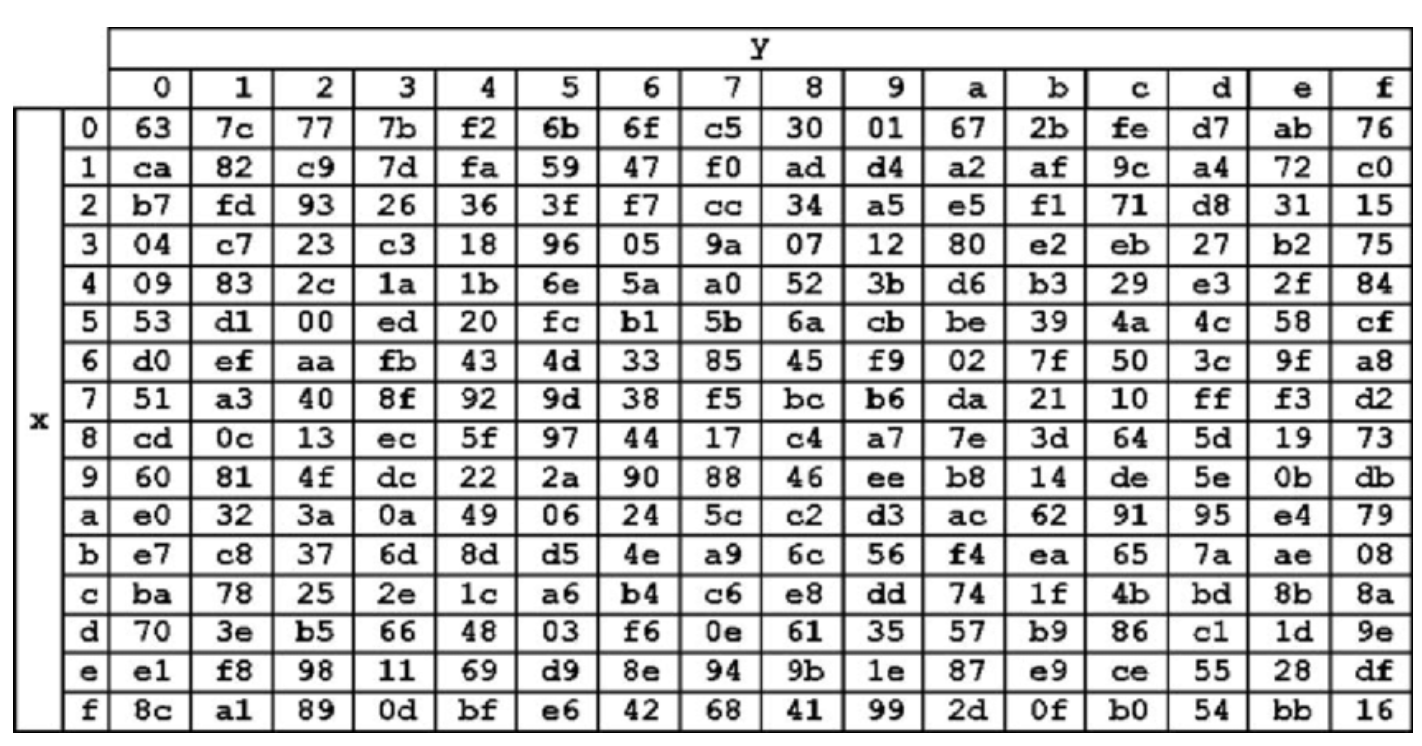
- S-box 생성 방법
- 의 에서
각 원소의 곱셈에 대한 역원을 구한 후,
비트 단위의 affine transformation을 수행
- 의 에서
-
ShiftRows 연산
- 각 행을 왼쪽으로 순환 시프트
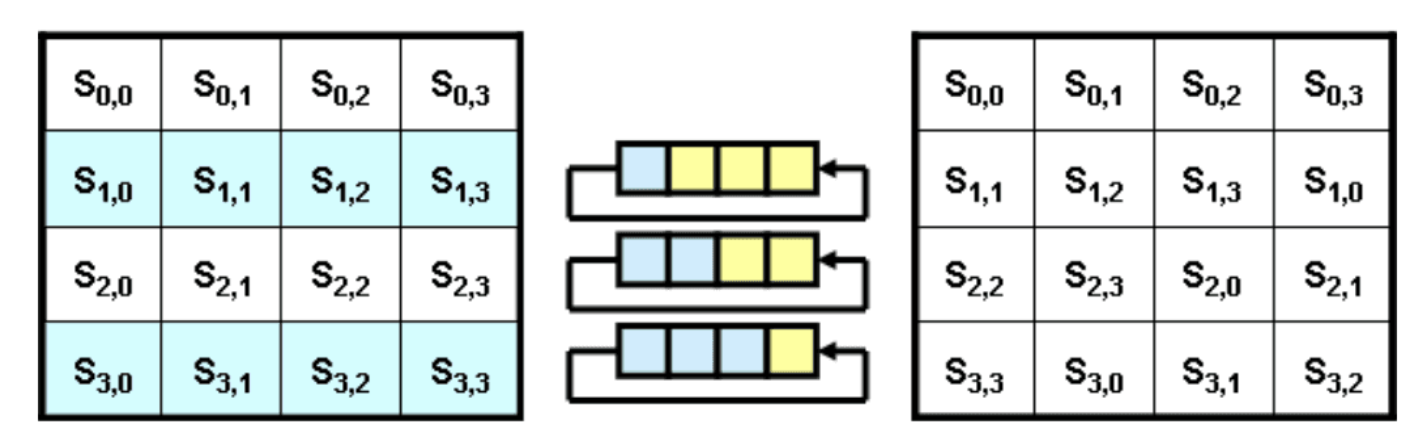
- 각 행을 왼쪽으로 순환 시프트
-
MixColumns 연산
-
각 열을 행렬곱으로 혼합
-
*
-
-
AddRoundKey 연산
-
state와 round key를 XOR 연산
-
-
마) 마지막 라운드
-
SubBytes 연산
- 비선형성을 갖는 S-box를 state에 적용하여 바이트 단위 치환
-
ShiftRows 연산
- 각 행을 왼쪽으로 순환 시프트
-
AddRoundKey 연산
- state와 round key를 XOR 연산
Mix Columns 연산은 하지 않는다
바) 종료화
- 행렬인 state를 16 bytes (128 bits)의 출력데이터로 변환
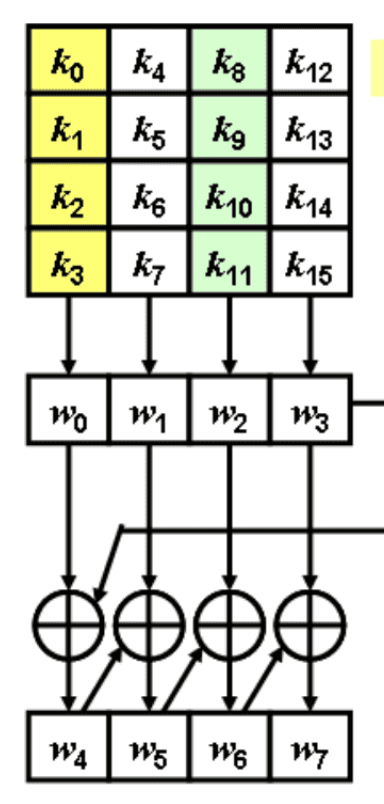
사) 라운드 키 생성
-
11개 필요: 초기화 와 각 라운드 ~
-
한 라운드 키가 4 words ( 16 bytes )이므로
총 44 words ( ~ ) 생성 후
4 words 씩 라운드 키로 사용- = ~
-
~