대학원

(입출력) 0개 이상의 외부 입력, 1개 이상의 출력(명확성) 각 단계는 모호하지 않고 단순 명확해야함(유한성) 한정된 수의 작업 후에는 반드시 종료(유효성) 모든 명령어는 수행 가능해야함.(실용적 관점) 효율적이어야 함.설계표현 / 기술일상 언어순서도의사코드프로그래밍

주어진 문제의 해를 구하는 일련의 선택 단계마다 전후 단계의 선택과는 무관하게해당 단계에서 가장 최선이라고 볼 수 있는 선택을 통해 전체적인 최적해를 찾는 설계기법국부적인 최적해 ( 로컬 해 )가 전체의 최적해를 이끈다.최적성의 원리를 만족.고객에게 돌려줄 거스름 돈이

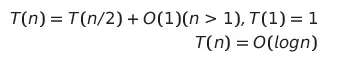
순환적으로 문제를 푸는 하향식 (Top - Down)설계 방법분할된 작은 문제들의 각 해를 구하고, 해를 결합하여 원래의 문제의 해를 구함분할된 소문제는 원래 문제와 동일단, 입력 크기만 작아짐분할된 작은 문제는 독립적순환적 분할 및 결과의 결합이 가능주어진 문제를 여

주어진 문제를 여러 개의 부분 문제로 분할문제의 크기가 작은 부분 문제에 대한 해를 저장해 놓고,이를 이용하여 크기가 보다 큰 문제의 해를 상향식으로 만들어가는 설계 기법.부분 문제가 독립적이지 않음부분 문제를 분할하면 중복/공통된 부분 문제를 포함한다.중복된 부분 문

삽입, 삭제, 탐색 연산이 지원되는 동적 자료구조일반적인 배열 개념을 일반화 시킨 것레코드.key -> 매핑 함수 -> 테이블의 인덱스(주소)최악 $O(n)$, 평균 $O(1)$키 값 자체를 해시 테이블의 인덱스로 사용$key -> Tkey$key$U = {0, 1,

한 함수와 다른 함수를 반전 이동한 값을 곱한 다음,구간에 대해 적분하는 연산$$(f\*g)(i)=\\int\_{\\infty}^{-\\infty}{f(\\tau)g(t - \\tau)d\\tau}$$1차원 Convolution$S(i) = (I \* K)(i) = \

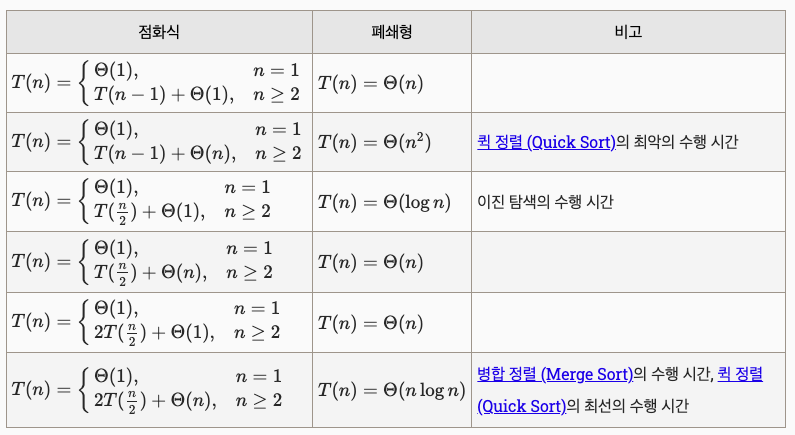
알고리즘의 시간 복잡도를 분석하는 기법연산의 수행 횟수/시간이 독립적으로 결정되지 않고 가변적인 경우앞서 수행된 연산에 따라 실행 시간이 달라질 때,실제 최악 수행 시간을 보다 더 정확하게 분석하는 방법.합계 분석알고리즘에서 해당 연산의 호출 전체에 대한 최악의 수행시

텍스트에서 패턴이 나타나는 모든 위치를 찾아내는 문제텍스트 $T0..n-1$, 패턴 $P0...m-1$, $n > m$알파벳 $\\sum$ -> 문자의 집합스트링 (문자열) -> 문자가 연속적으로 나열된 것텍스트가 자주 바뀌고 찾는 패턴의 길이가 짧은 경우텍스트는 고졍

다중 키워드 매칭 알고리즘으로,주어진 패턴들을 이용하여 단어 나무를 생성하고텍스트를 왼쪽에서 오른쪽으로 스캔하면서 단어 난무에서 패턴을 매치 시킴$O(m_s + n)$패턴의 집합 $P={P_1, P_2, ..., P_q}$$m_s = \\vert P_1 \\vert +

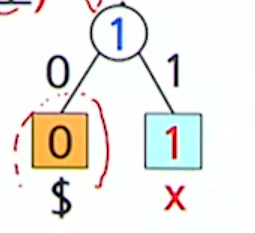
주어진 데이터의 의미를 바꾸지 않으면서,더 적은 저장 공간에 효율적으로 기록하기 위함.인코딩 전의 데이터 크기와 인코딩 이후 데이터 크기의 비율$\\frac{\\vert C \\vert}{\\vert S \\vert}$인코딩 전의 데이터 크기에 비해 인코딩을 통해 줄어

컴퓨터의 이론적 모델무한한 길이의 테이프, 유한한 개수의 기호와 상태상태와 기호에 따른 헤드의 동작을 정해둔 규칙현재 상태와 읽은 기호에 따라 헤드가 테이프에 기호를 쓰거나 좌우로 이동알고리즘의 수행 시간이 입력 크기 n에 대한 다항식으로 표현되는 알고리즘$O(n),

군(G, +)아래 성질들을 만족하는 집합 G와 이항연산 +$a, b \\in G$ 라면,$a + b \\in G$모든 $a,b, c \\in G$에 대해$(a+b) + c = a + (b + c)$$e + a = a + e = a$인 $e$가 존재각 $a \\in G$

1. 특징 추출(Feature Extraction) > Data A set of samples $(D = \{xi\}{i=1...N}, D=\{(xi, yi)_{i=1...N}\})$ Goal of Learning 분석에 필요한 정보만 추출 (구체적 분

지도학습, 교사학습이라고 한다.학습할 때 목표 출력 값 (target ouput)이 함께 제공된다.학습을 안내하고 지도해주는 supervisor(교사)가 존재$D = {(xi, y_i)}{i=1,....N}$분류문제와 회귀문제에 적합하다.Bayes 분류기, K-NN 분

암호화와 복호화에 하나의 같은 키를 사용하는 암호 시스템대칭키, 비밀키, 단일키, 관용암호 등과 같은 이름으로 불리기도 한다.$C = E_K(P)$ : 암호화$P$ : 평문$K$ : 키$C$ : 암호문$P = D_k(C)$: 복호화$P$ : 평문$K$ : 키$C$ :

1. K-NN Classifier > 2. Characteristics

임의의 수암호학에서 중요하게 사용됨.특히 다양한 상황에서의 키에 활용예)One-Time-Pad의 키평문의 길이와 동일하며 반복되지 않는 랜덤 키한 번 사용된 키는 다시 사용하지 않고 버림무작위성 (randomness)균일 분포생성된 수열의 비트 분포가 균일해야함독립성수

asdasd2\.