[Data_Structure] Graph

먹보·2022년 12월 27일

MUK_BO's Data_Structure & Algorithm

목록 보기

7/15

✍ 정의

그래프는 겉으로 보기에는 복잡하게 얽혀있는 지하철 노선도처럼 보이지만 쉽게 얘기하자면, 부모, 자식, 그리고 뿌리의 개념이 없는 TREE구조와 비슷하며 Node(정점 또는 Vertex)과 간선(Edge)으로 이루어져 있다.

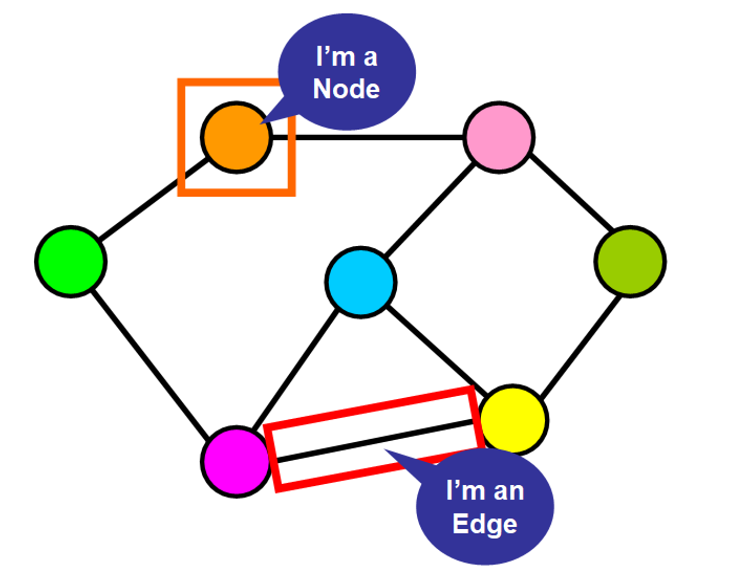
NODE(정점) : 그래프를 구성하는 ELEMENT 또는 VERTEX
EDGE(간선) : 각 NODE를 연결하는 다리

이 때, 정점에서 다른 정점으로 나가는 간선을 해당 정점의 outdegree라고 하며 들어오는 간선을 해당 정점의 indegree라고 합니다.

그래프는 소셜 네트워크, 교통 시스템 및 정보 흐름과 같은 다양한 실제 문제를 모델링하는 데 사용할 수 있습니다.

✍ 그래프의 유형

다양한 유형의 그래프가 있지만 가장 일반적인 유형은 다음과 같습니다.

📝 DIRECTED GRAPH : 방향 그래프

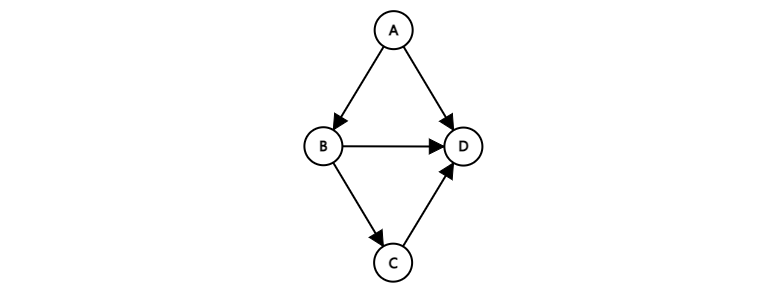
노드 간에 방향성을 가진 채 연결이 되어 있다.

📝 UNDIRECTED GRAPH : 무방향 그래프

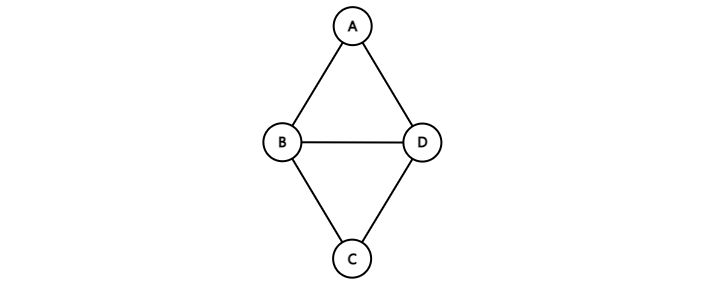
노드 간 서로 연결만 되어 있으며 방향성은 중요하지 않다.

📝 Weighted Graphs : 가중치 그래프

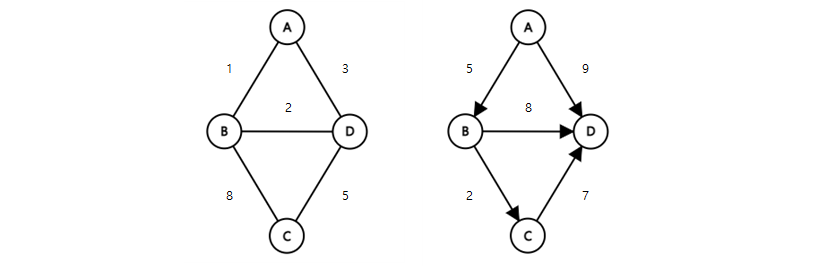
우선 여기서 가중치란, 노드와 노드 사이에 드는 비용을 뜻합니다. 이런 가중치 값이 노드를 잇는 간선에 부여된 그래프를 가중치 그래프라고 합니다.

📝 Complete Graph : 완전 그래프

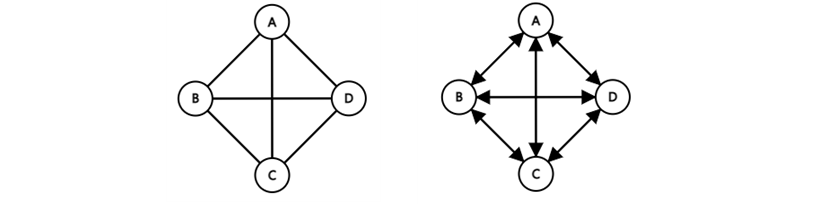
완전 그래프란 그림에서도 알 수 있듯이 하나의 노드가 존재하는 다른 모든 노드에 연결되어 있는 그래프를 말합니다.

이 밖에도 부분 그래프, 연결 그래프, 단절 그래프 등이 있습니다.

📝 자바스크립트를 활용한 그래프

class Graph {
  constructor() {
    this.vertices = [];
    this.edges = {};
  }

  addVertex(vertex) {
    this.vertices.push(vertex);
    this.edges[vertex] = [];
  }

  addEdge(vertex1, vertex2) {
    this.edges[vertex1].push(vertex2);
    this.edges[vertex2].push(vertex1);
  }

  printGraph() {
    let graph = "";
    for (let i = 0; i < this.vertices.length; i++) {
      graph += this.vertices[i] + " -> ";
      let neighbors = this.edges[this.vertices[i]];
      for (let j = 0; j < neighbors.length; j++) {
        graph += neighbors[j] + " ";
      }
      graph += "\n";
    }
    console.log(graph);
  }
}

자바스크립트를 활용해서 그래프 자료 구조를 만들어보았다.

진관적으로 알 수 있도록 메서드 이름들을 짤막하게 표현했으며.

Vertex를 추가 후 Edge로 연결해 주고 나서 그래프를 그려보면 다음과 같이 출력된다.

A.addVertex('A')
A.addVertex('B')
A.addVertex('C')
A.addVertex('D')
A.addVertex('E')

A.addEdge('A','B');
A.addEdge('B','C');
A.addEdge('C','D');
A.addEdge('D','E');
A.addEdge('A','D');
A.addEdge('C','E');

A -> B D 
B -> A C 
C -> B D E 
D -> C E A 
E -> D C