
✍️ 정의
TREE는 그래프 중 하나로 단어 뜻 그대로 자료구조의 데이터 저장 형태가나무처럼 생겨 노드와 간선으로 이루어져 있다. 하나의 시작 점에서 나뭇가지처럼 여러 갈래로 뻗어 나고 또 그 갈래에서 여러 갈래로 갈라지는 듯 일종의 계층적 데이터의 집합입니다.
=> 참고로, 트리로 이루어진 집합을 숲이라고 합니다.
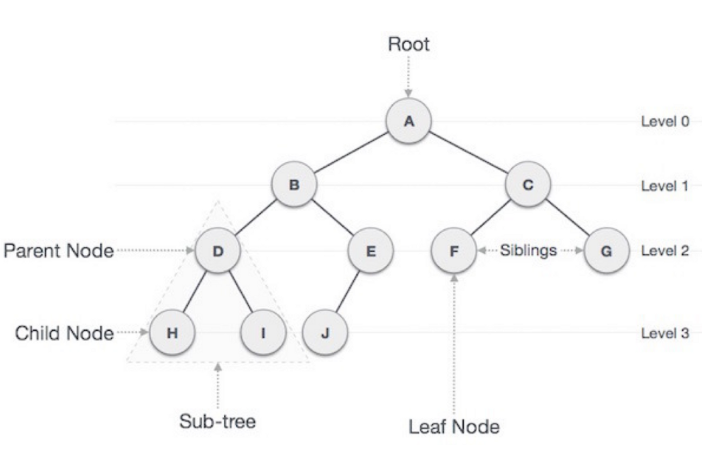
📝 TREE의 구조
TREE의 구조는 위 사진과 같으며, 각 부분은 특정 명칭을 가지고 있다.
- ROOT : 트리 구조의 시작점
- Parent Node : 특정 노드의 상위 노드
- Child Node : 특정 노드의 하위 노드
- Sibling Node : 특정 노드와 같은 계층에 있는 노드
- Leaf Node : 자식이 없으며 트리의 가장 끝에 있는 노드
- Level : 같은 ROW에 위치한 노드들의 집합
- Depth : ROOT에서 특정 노드까지의 최단 경로 개수
- Height : 트리의 높이느 루트 노드부터 리프 노드까지 거리 중 가장 긴 거리 (FROM ROOT TO LAST LEAF NODE)
TREE에는 여러가지 종류가 있는데 이건 추후 예제와 함께 업데이트 할 예정이다.
✍️ 종류
📝 이진 트리
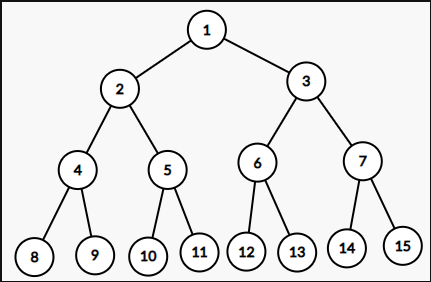
위 사진과 같이 이진 트리는 자식의 노드 수가 최대 2개인 트리를 의미하며 여러개로 분류 할 수 있습니다.
-
정이진 트리 (FULL BINARY TREE) : 자식 노드가 0 또는 2개인 트리
-
완전 이진 트리 (COMPLETE BINARY TREE) : 왼쪽에서부터 채워져 있는 이진 트리
-
변질 이진 트리 (DEGENERATE BINARY TREE) : 자식 노드가 하나 밖에 없는 이진 트리 (한 줄로 연결 되어 있는 트리)
-
포화 이진 트리 (PERFECT BINARY TREE) : 모든 노드가 꽉 차 있는 이진 트리
-
균형 이진 트리 (BALANCED BINARY TREE) : 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리
📝 이진 탐색 트리
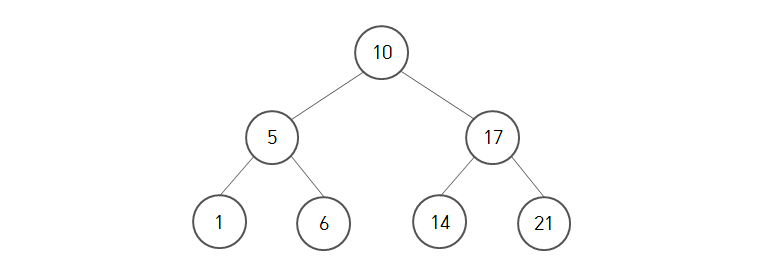
위 사진과 같이 이진 탐색 트리 (BST)는 노드의 오른쪽 하위 트리에는 '노드 값보다 큰 값'이 있는 노드만 포함되고, 왼쪽 하위 트리에는 '노드 값보다 작은 값'이 들어 있는 트리를 뜻합니다.
=> 균형이 용이하다는 가정 하에 최고의 효율을 보여 줄 수 있습니다.
- 탐색: O(n) [선형적], O(log n) [Best Case]
- 삽입: O(n) [선형적], O(log n) [Best Case]
- 삭제: O(n) [선형적], O(log n) [Best Case]
📝 AVL 트리
AVL (ADELSON-VELSKY AND LANDIS TREE) 트리는 앞서 설명한 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리입니다. 항상 두 자식 서브트리의 높이가 최대 1만큼 차이난다는 특징을 가지고 있습니다.
- 탐색: O(log n)
- 삽입: O(log n)
- 삭제: O(log n)
📝 레드 블랙 트리

레드 블랙 트리는 위 사진과 같이 균형 이진 탐색 트리에서 색상을 나타내는 비트 값이 포함된 트리입니다. AVL 트리와 같이 탐색, 삽입, 삭제에 대한 시간 복잡도가 모두 O(log n)이며 삽입 및 삭제 중에 트리가 균형을 유지하도록 하는데 사용 됩니다.
- 탐색: O(log n)
- 삽입: O(log n)
- 삭제: O(log n)
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
if (!this.root) {
this.root = newNode;
return this;
}
let current = this.root;
while (true) {
if (value === current.value) return undefined;
if (value < current.value) {
if (!current.left) {
current.left = newNode;
return this;
}
current = current.left;
} else {
if (!current.right) {
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value) {
if (!this.root) return undefined;
let current = this.root;
while (true) {
if (value === current.value) return current;
if (value < current.value) {
if (!current.left) return undefined;
current = current.left;
} else {
if (!current.right) return undefined;
current = current.right;
}
}
}
}이진 트리를 코드로 한 번 구성해봤다 생각보다 트리구조를 이해하는데 도움은 되었지만 그 만큼 시간이 오래 걸린 것 같다.
