1. Model Representation

복습: 학습 알고리즘에는 회귀 문제, 분류 문제가 있다.

Notation

앞으로 다음과 같이 변수를 많이 사용할 것이므로, 간단한 예를 통해 익히도록 하자!

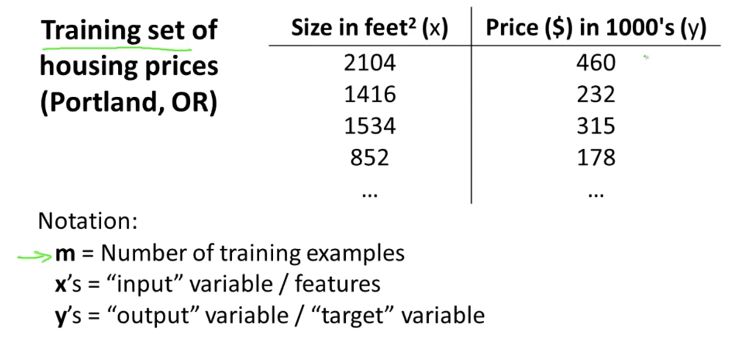
• m = Number of training examples
• x's = "input" variable / features
• y's = "output" variable / "target" variable
• (x,y) = a training example
• (x(i), y(i)) - 지수가 아니라 super script(=index) 예제 data set에서 몇번째 행,열인지 알려주는 것.

Linear regression with One Variable

더 복잡한 알고리즘에 들어가기 전에 선형 회귀, 다른 말로 단일변량(univariate) 선형 회귀에 대해 배워보자. univariate는 one variable을 fancy하게 표현하는 단어이다. 즉 하나의 값을 넣었을 때, 하나의 결과 값을 내보내는 것(=1차 함수)이다.

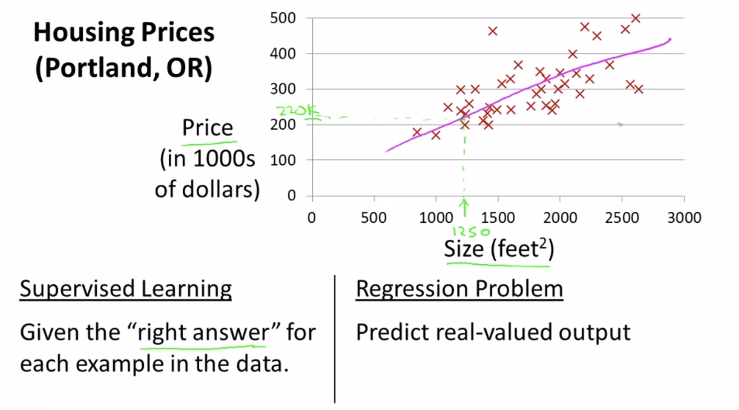
training data set 을 learning algorithm에 넣었을 때, learning algorithm이 하는 일은 함수(보통 convention으로 h=hypothesis라 쓴다고 함)를 만들어낸다.

h: X -> Y so that h(x) is a goot predictor for the corresponding value of y

h 함수의 역할은 input(x)에 따른 output(estimated value of y)을 도출해내는 것이다. (h is a function that maps from x's to y's)

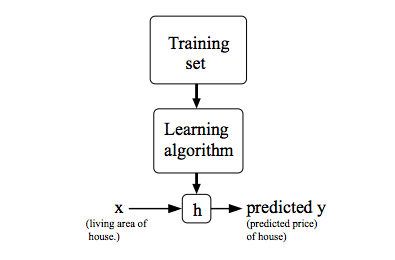
algorithm을 디자인할 때, 그 다음으로 해야할 일은 가설 h를 어떻게 표현할 것인가이다. 아래 식은 x의 선형 함수인 y를 예측하는 것으로 해석하면 된다.

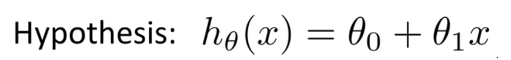
• 세타는 생략하기도 한다
• 1차 방정식을 배웠을 때를 떠올려보면... 세타0을 기울기, 세타1을 y절편ㅋㅋ으로 보면 될 것 같다.

2. cost function J

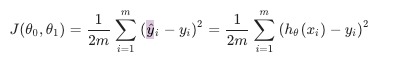
비용 함수를 사용하면, 우리가 세운 h 함수의 정확도를 측정할 수 있다. 평균을 좀더 멋 있게 나타낸 말이라고 한다. 비용 함수는 오차 함수의 제곱(squared error function.)이라고도 불린다.

h(x)는 내가 예측한 y 값이고, y는 실제로 가지고 있는 data set이다. 예측한 값과 실제 값의 차이들을 모두 더함으로써 오차를 예측하려고 하는 함수인데, 여기서 제곱은 뺀 값을 양수화 시키기 위한 과정 같고, 2m으로 나눈 것은 경사 하강법을 위해 편의상 넣은 것이라고 한다.

Gradient descent(경사 하강법)
1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다.

결론적으로 내가 예측한 결과 값과 training set 간의 오차를 최소화하는 세타0, 세타1을 구하는 것이 비용 함수 J라고 할 수 있다.

2.1 Intuition I

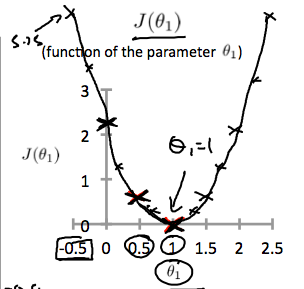
비용 함수 J에 대해 더 직관적으로 알아보기 위해 variable을 하나만 가진 세타1 함수(0,0을 지나는 1차 함수)를 예시로 들어보자.

아래 예시에서 왼 쪽은 내가 알고리즘으로 예측한 h함수이고 오른쪽은 세타 값에 의한 비용 함수 J이다.

1. 세타1 = 1일 때 ( h = 기울기가 1이고 0,0을 지나는 함수)
   

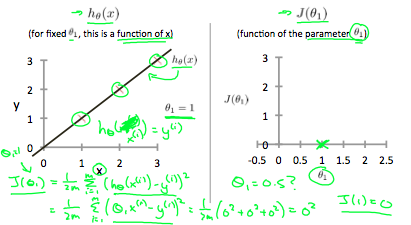
2. 세타1 = 0.5일 때 ( h = 기울기가 0.5이고 0,0을 지나는 함수)
   

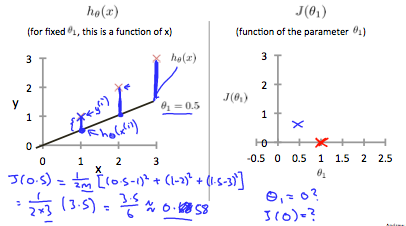
세타값에 따른 J함수값을 점으로 연결하면, 결과적으로 아래와 같은 2차 함수가 만들어진다. 그리고 최소값은 세타1이 1일때 꼭지점에서 가장 작은 값이며, 이는 h 함수의 기울기가 1인 선형 함수를 뜻한다.

2.2 Intuition II

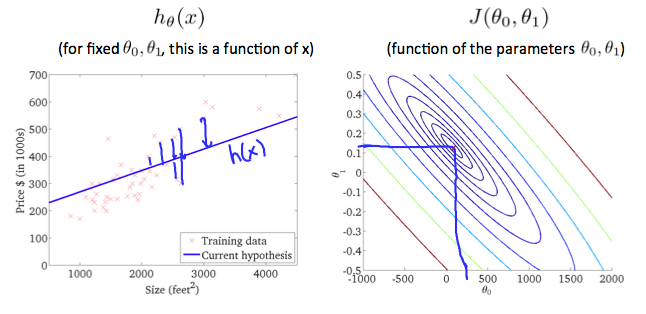
위에서는 변수가 하나일 때를 조건으로 두었지만, 만약 세타0까지 존재하는 함수일 때는 어떨까? 변수가 3개(세타0, 세타1, J결과값)인 만큼 처음에 3차원 그래프를 보여줬지만, 그보다는 등고선 그래프를 많이 쓴다고 한다.

A contour plot is a graph that contains many contour lines. A contour line of a two variable function has a constant value at all points of the same line. An example of such a graph is the one to the right below.

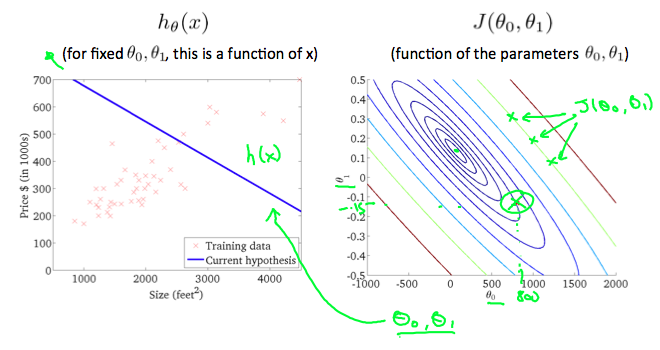
3차원 그래프를 평행으로 자른 느낌이기 때문에, 결국 최소값은 제일 가운데에 있는 꼭지점이 되게 된다.