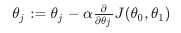training set을 통해 최적의 결과를 내는 선형 회귀 함수(가설 함수 h)를 도출하기 위해, h의 파라미터(세타 1,2,3...)를 input, 예상값과 실제값의 차를 제곱한 합을 output으로 도출하는 비용 함수 j의 최저점을 찾는 과정 중에 있다.

gradient descent equation을 통해 결국은 미분 계수가 0이 되는 파라미터 값을 구하는 것이 이번 장의 목표다.

1. Gradient Descent

비용함수가 2차원 함수라면 꼭지점을 구해 값을 계산할 수 있지만, parameter가 2개 이상일 경우 3차원 이상의 그래프가 되기 때문에 앞서 2장에서 얘기했던 Gradient Descent, 즉 경사 하강법을 사용해 최저점을 구해야 한다.

we have our hypothesis function and we have a way of measuring how well it fits into the data. Now we need to estimate the parameters in the hypothesis function. That's where gradient descent comes in.

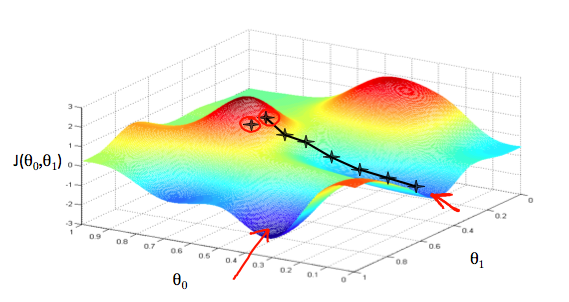
위 그림에서 붉은 색 화살표로 표시된 부분이 최소값local minima 지점들이다. 비용 함수에서 시작 점을 잡고, 해당 값의 부분 미분 계수(=1차 함수의 탄젠트 값)를 구하면 해당 기울기 J함수와 만나는 지점으로 다음 시작점을 잡아서 이동하는 방식이다.

강의 노트에서 minima라고 써져있어서 오타인줄 알았더니, 최소값이 아닌 지역적인 최소값에 대해서 minima라고 부른다고 한다.

따라서 미분 계수는 방향을 알려주고, 얼마나 움직일 지는 parameter 알파(=learning rate)에 의해 결정된다. 알파값이 클 수록 많이 움직이고, 작을 수록 적게 움직인다. 어디에서 출발하는지에 따라 다른 최저점에 도달할 수 있다.

The gradient descent algorithm is: repeat until convergence: 동일한 값으로 수렴할 때까지 다음 알고리즘을 반복하게 된다. 특정 지점의 비용 함수에서 부분 미분 계수 * learning rate(보폭 정도로 해석)를 뺀 값으로 비용 함수값을 다시 할당하고,이 과정을 계속 반복하는 것!

주의할 점

parameter들은 동시에 업데이트가 되어야 한다. 만약 하나씩 업데이트가 되면 바뀐 변수가 들어가버리기 때문에 오류가 생길 수 있다. 완전히 잘못된 건 아니지만 일반적으로 동시에 업데이트 해준다고 한다.

아래에서 := 표시는 변수 할당 개념으로 보면 된다. equal이 아닌 assign이고, python 문법으로 본다면 := 는 =, 같다는 ==로 해당 기호와는 분리해서 보아야 한다.

2. Intuition

parameter가 하나가 있다고 가정하고 gradient descent 알고리즘을 더 잘 이해해보자. 공식은 다음과 같고, 최소값에 도달할 때까지 공식을 반복할 것이다.

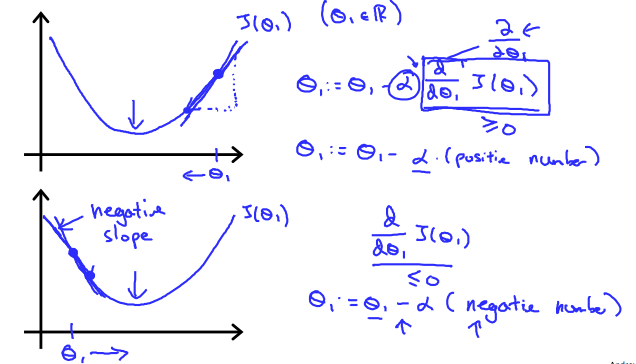
만약 기울기가 양수일 경우 기존 기울기에서 값을 빼주게 되어 기울기 값이 점점 작아지게 되고(완만하게 되고), 기울기 값이 음수일 경우 기존 기울기 값에서 더해지게 되기 때문에 기울기가 가팔라진다.

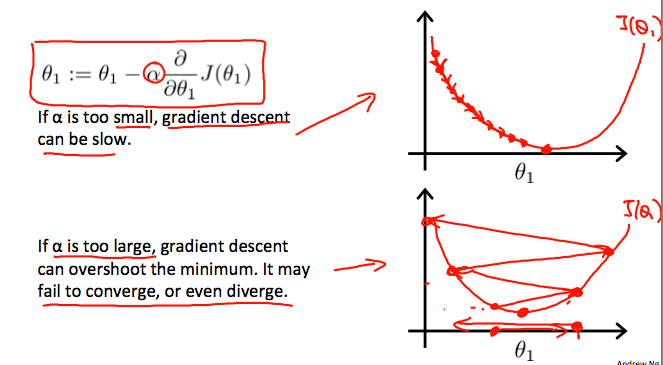
learning rate(알파값)도 알고리즘이 적당한 시간에 수렴할 수 있도록 잘 조절해야 한다. 너무 크거나 작을 경우 step size가 맞지 않을 수 있다.

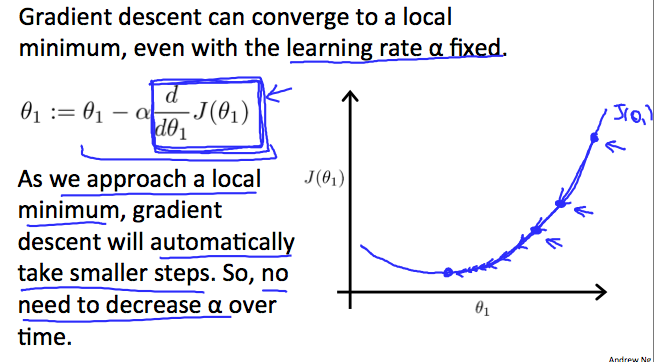
알파가 고정되어 있는데 수렴할 수 있는 이유

최소값에서 기울기가 0이 되기 때문에, learning rate를 따로 조절해줄 필요가 없이 gradient descent는 자동적으로 smaller step을 가게 된다. 결국에는 다음과 같이 될 때까지 수렴한다고 보면 된다.

3. Gradient Descent for linear regression

머신 러닝 알고리즘으로 도출해낼 가설 함수 h(x)와 비용 함수를 gradient descent equation에 적용해보면 다음과 같다. m은 training set의 크기이고, 세타1과 세타0은 동시에 바뀌는 기울기 값들 x(i), y(i)는 training set의 결과값들이다.

세타0은 가설 함수 h에서 상수항이지만, 세타1의 경우x값에 따라 바뀌는 parameter이기 때문에 미분을 위해 끝에 x(i)를 곱해줬다. 이유를 설명해주는 간단한 예시라는데 ... 아직 아래 식은 솔직히 이해가 잘 안 간다.

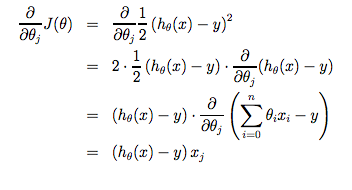
🔥 point

어쨌든 가설에 대한 추측으로 시작해서 경사 하강 방정식을 계속 사용하다 보면, 가설은 점점 정확해진다는 점이다.

batch gradient descent

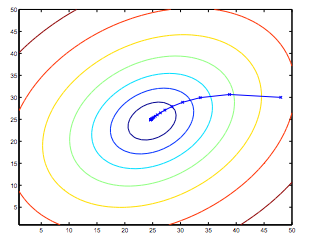
집단 기울기 하강. 기울기 하강 시 모든 훈련 예제를 지나는 것을 말한다. 아래 그래프를 예시로 들어 보면, 해당 방법의 경우 스텝마다 모든 training set(모두 다른 색깔의 선들)을 거쳐가게 된다. 요런 것들을 batch gradient descent라 부른다고 한다.

일반적으로 경사하강은 지역적으로 여러 최소값을 가지지만, 해당 함수는 하나의 global minimum에 도달한다.

batch : 모델을 학습할 때 한 회당 사용되는 example set의 모임