
> 문제
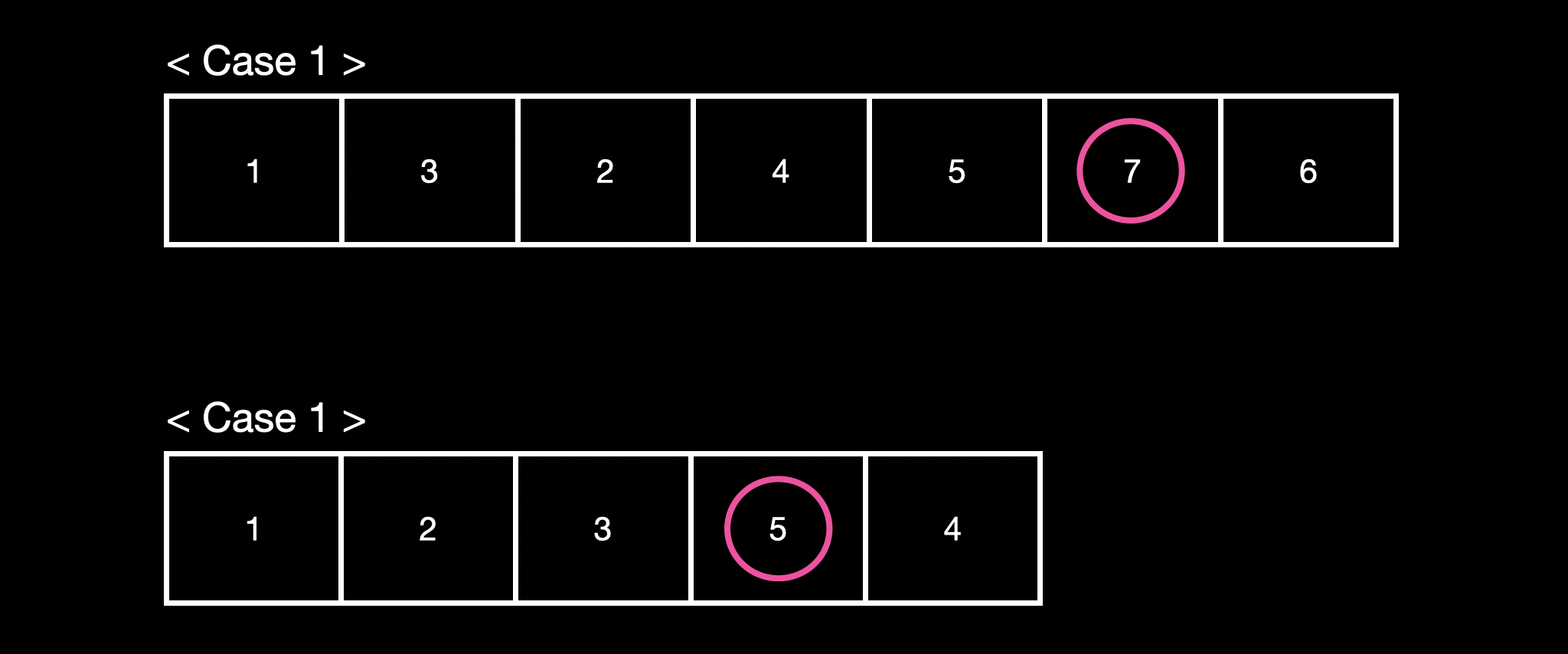
주어진 배열에서 특정 index를 기준으로 양측의 수보다 큰(예외: 마지막 숫자의 경우 왼쪽의 숫자와만 비교) 숫자 중 가장 큰 수의 index를 리턴하는 문제입니다.
> solution
주어진 문제의 경우 중간 index를 기준으로 오른쪽에 큰 값이 있기 때문에 binary search로 다음과 같이 해결할 수 있습니다.
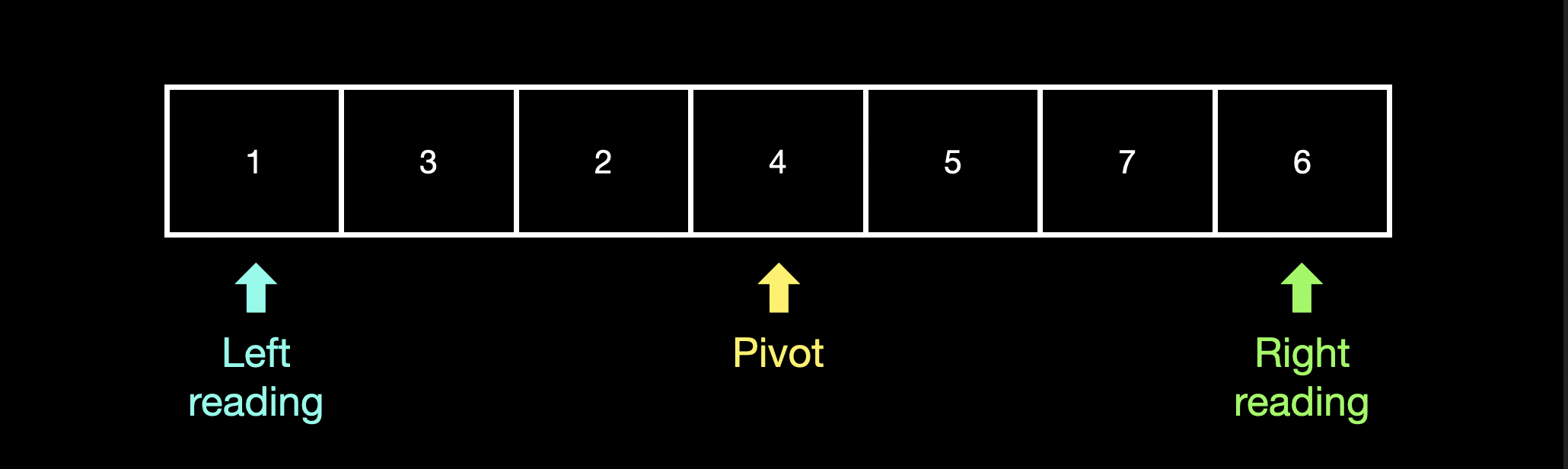
시작을 기준으로
"left_reading"은 index 0을 가리킵니다.
"right_reading"은 배열의 가장 끝 index를 가리킵니다.
"pivot"은 left_reading와 right_reading의 중간 index를 가리킵니다.
pivot이 위치한 index의 값보다 pivot의 오른쪽 index가 가리키는 값이 "크면" left_reading을 pivot +1 해주고, "작으면" right_reading을 pivot의 index와 같게 해주는 것이 한 번의 동작입니다.
right_reading의 index가 left_reading의 index보다 클 때 까지 반복합니다.
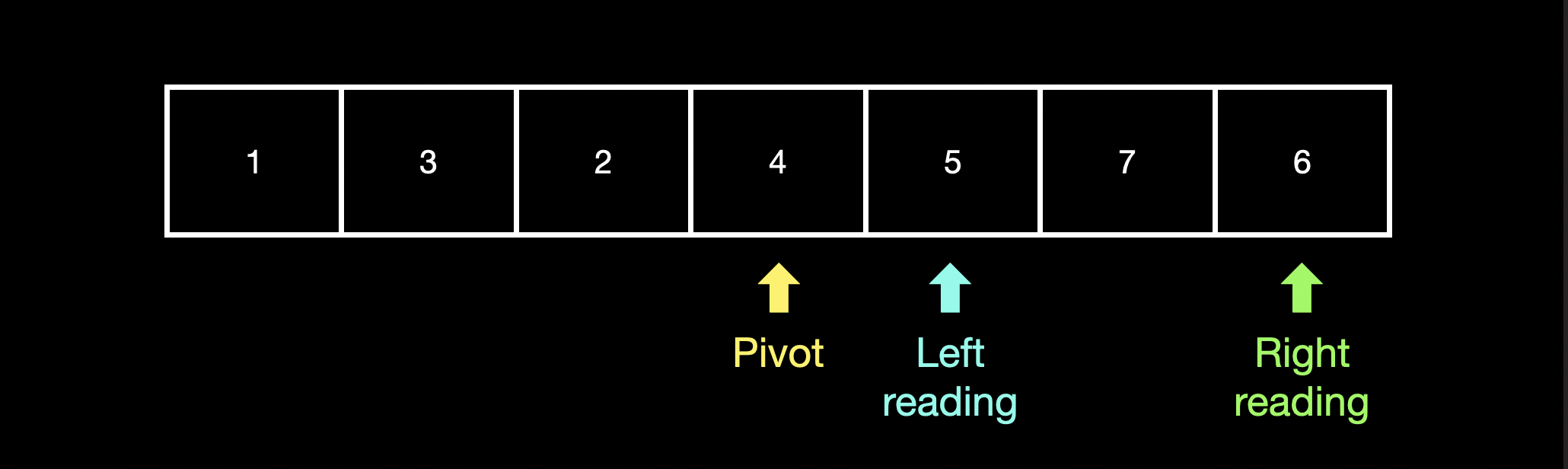
pivot 오른쪽의 값이 pivot보다 크기 때문에 "left_reading"을 pivot의 오른쪽으로 이동시켜줍니다.

"pivot"은 left_reading와 right_reading의 중간 index로 이동합니다.
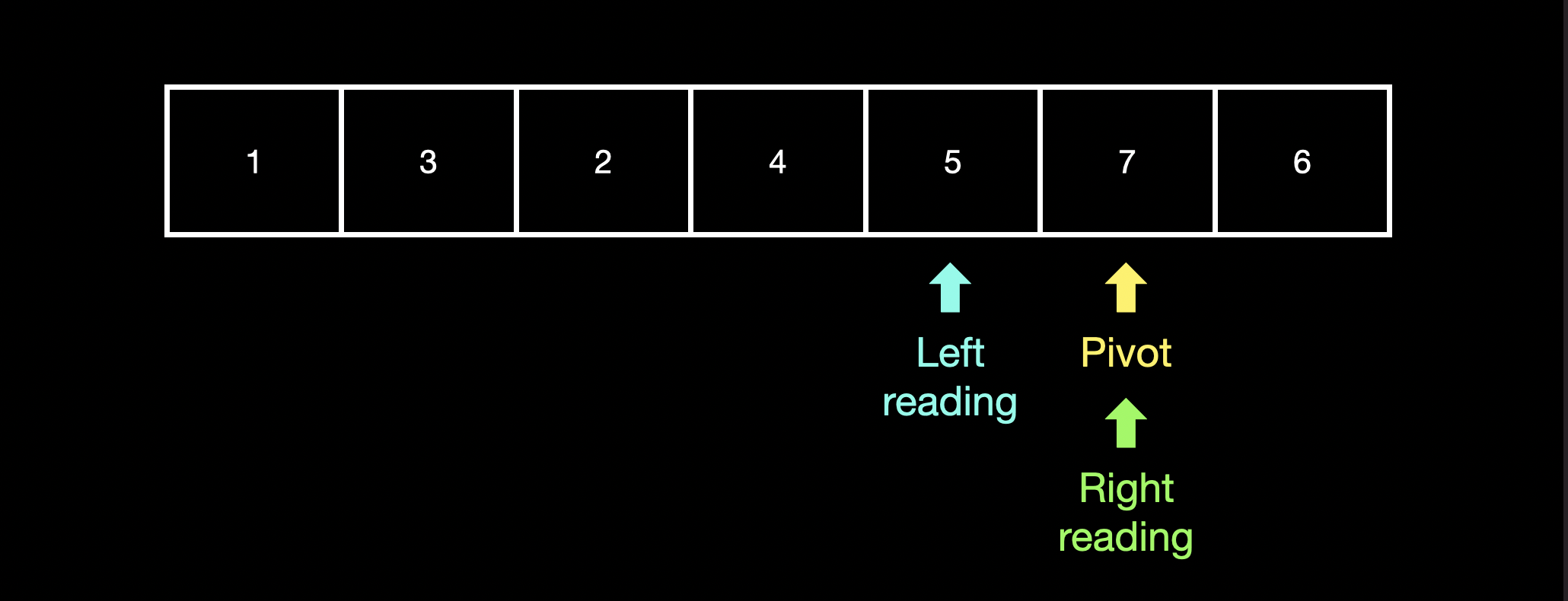
"pivot"의 오른쪽 값이 "pivot"이 위치한 값보다 작기 때문에 "right_reading"은 "pivot"의 위치로 이동합니다.
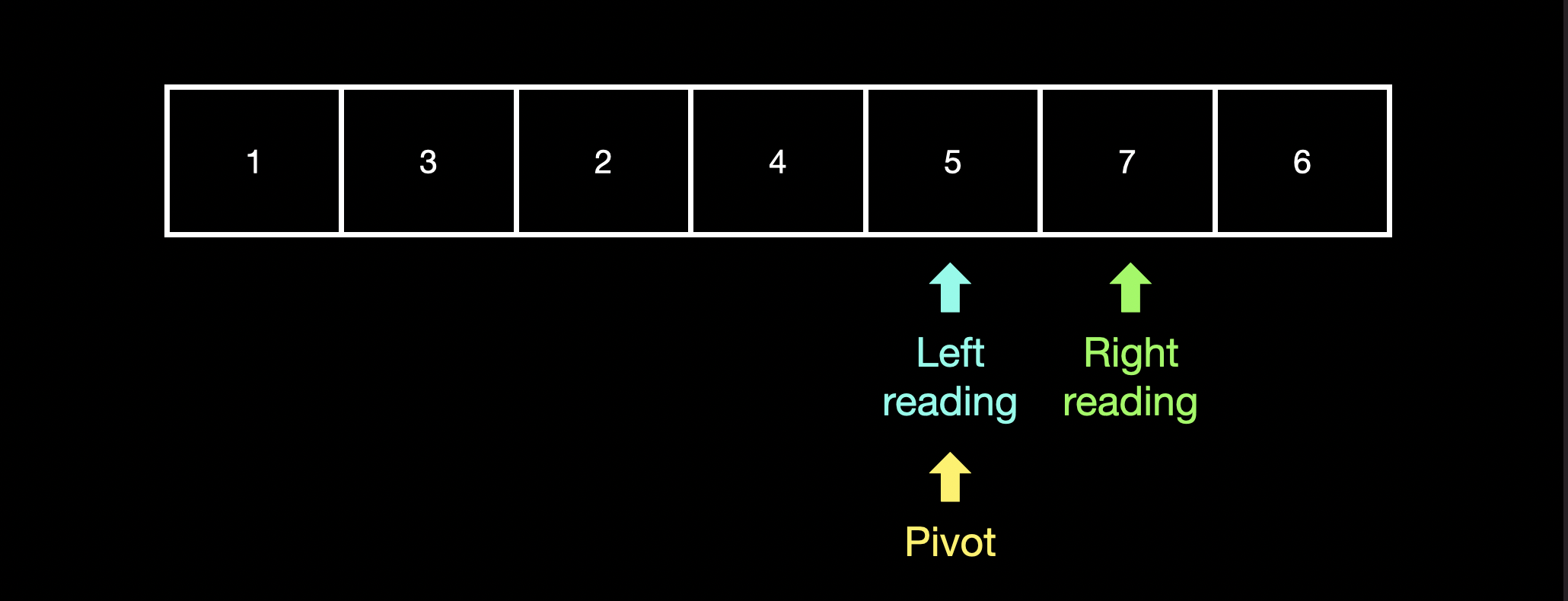
"pivot"은 다시 left_reading와 right_reading의 중간 index로 이동합니다.
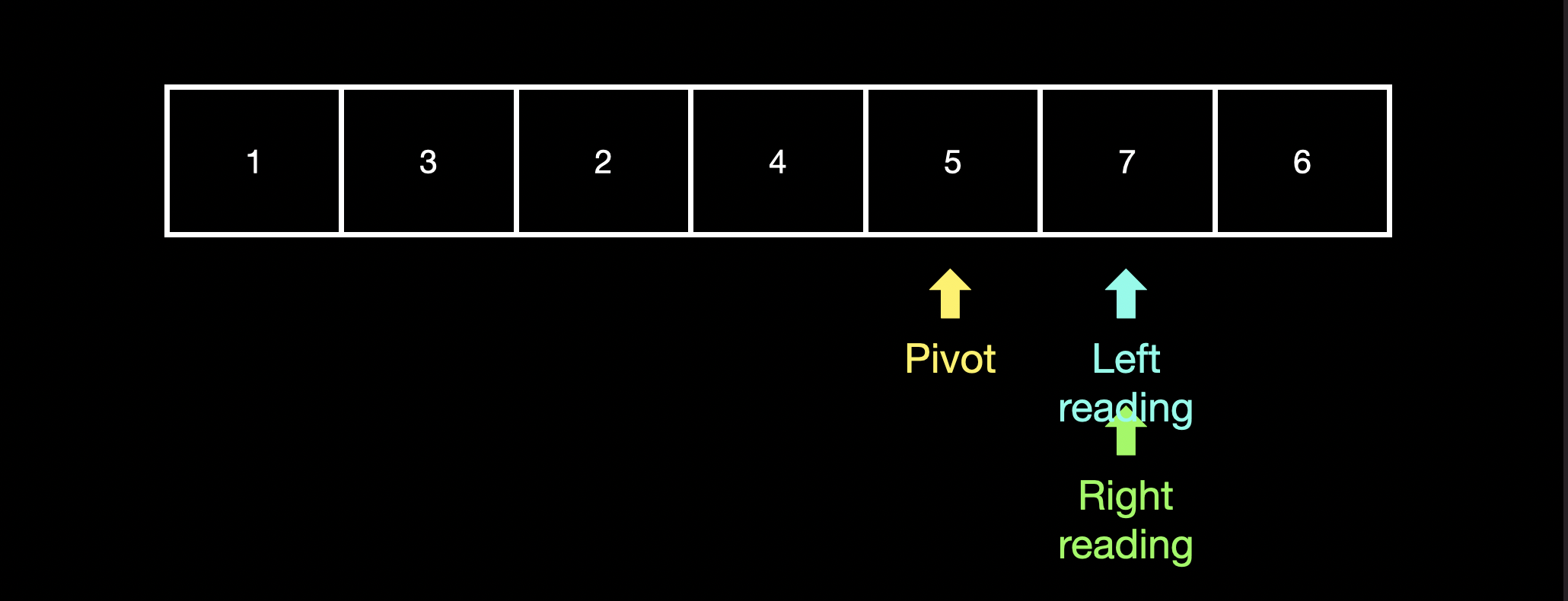
"pivot"의 다음 값이 "pivot"이 가리키는 값보다 크기 때문에 "left_reading"은 "pivot"의 다음 자리로 이동합니다.
"right_reading"의 index가 "left_reading"의 index와 같아지면서 최종 값으로 "left_reading"을 리턴하며 operation은 종료됩니다.
"left_reading"도 "right_reading"도 결국 마지막에 가장 큰 값을 가리키기 때문에 둘 중 어느 것을 리턴해도 상관 없습니다.
time complexity는 O(log n)입니다.
▶︎ code
arr = [1, 3, 2, 4, 5, 7, 6]
def find_peak_element(nums):
left_reading = 0
right_reading = len(nums) - 1
if len(nums) <= 1:
return 0
while left_reading < right_reading:
pivot = (left_reading + right_reading) // 2
num = nums[pivot]
next_num = nums[pivot + 1]
if num < next_num:
left_reading = pivot + 1
else:
right_reading = pivot
return left_reading
print(find_peak_element(arr))출처: 코드없는 프로그래밍
