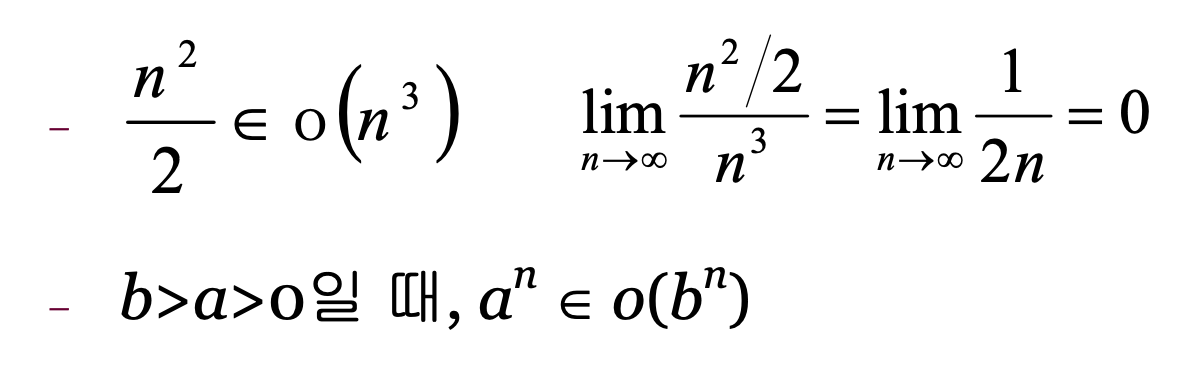[알고리즘] 개요

⭐알고리즘(algorithm)이란?

알고리즘은 문제를 해결하기 위한 단계별 절차이다.

분석(analysis) -> (Computational(=계산))알고리즘의 복잡성 ->Order

• 문제를 얼마나 효율적으로 해결하는지 결정하는 측도
  • Time - CPU cycles
  • Space - memory

⭐알고리즘 분석 예시) - 피보나치 수 구하기 알고리즘

예시 1) 재귀 방식

int fib (int n) {
   if (n <= 1)
      return n;
   else
      return fib(n-1) + fib(n-2);
}

Input size = n

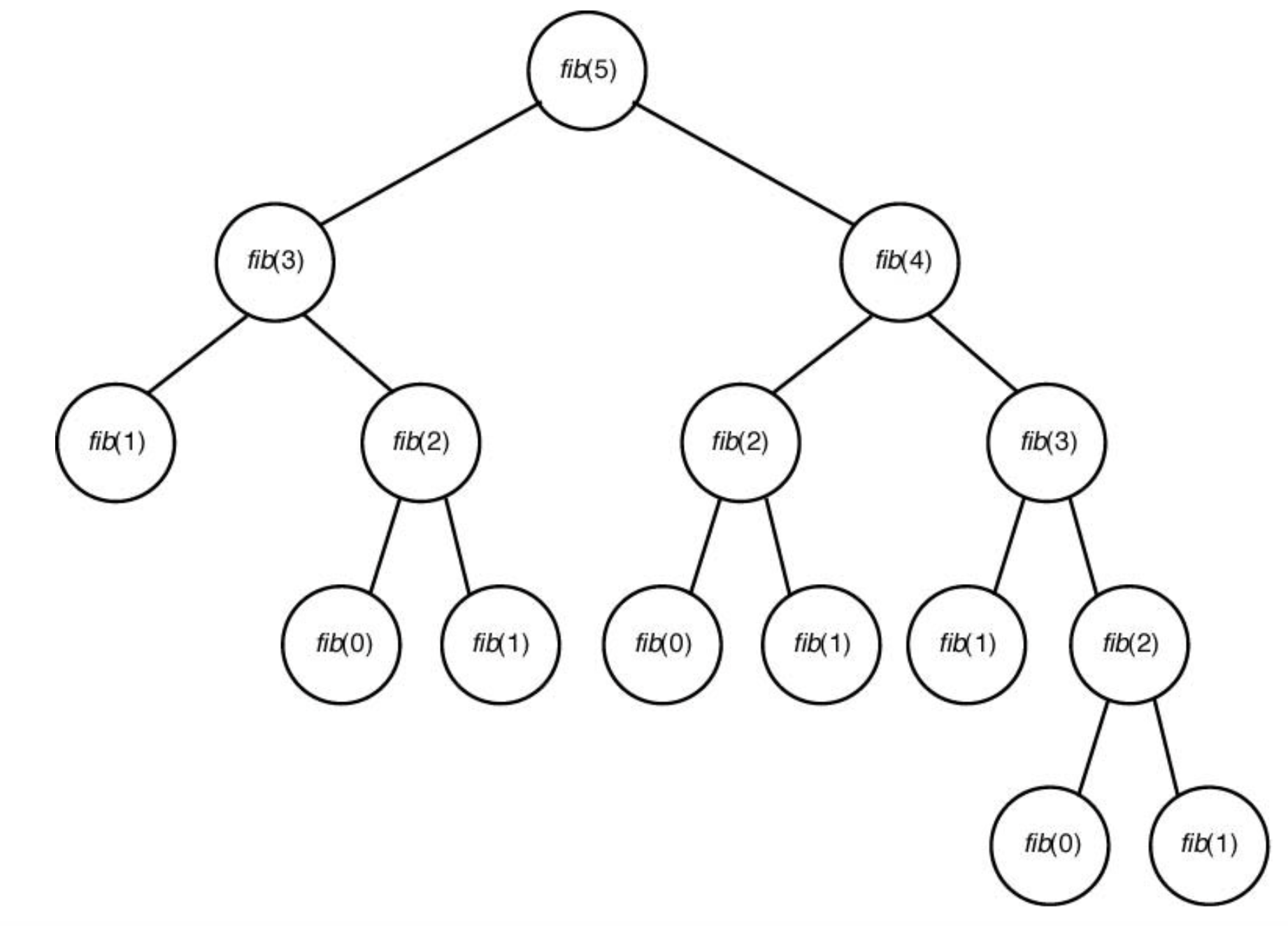
분석

T(n) = fib(n)을 계산하기 위하여 fib 함수를 호출하는 횟수
즉, 재귀 트리 상의 마디(node)의 개수가 기준이다.
T(0) = 1
T(1) = 1

• n이 2 이상일 경우
  $T(n) = T(n - 1) + T(n - 2) + 1$
  T(n - 1) >= T(n - 2)이므로 둘 다 T(n-2)로 통일
  $T(n) > 2 T(n - 2) \\ T(n)> 2^2T(n-4) \\ T(n) > 2^3 T(n-6) \\ ...\\ T(n) > 2^{n/2}T(0) \\ = 2^{n/2}$

증명 - 수학적 귀납법

예시 2) 반복문 방식

결국 반복문 방식의 알고리즘이 수행속도가 더 빠르다
이유: 중복 계산이 없이 배열에 저장하여 기억하기 때문에

⭐알고리즘을 분석 척도

• 시간 복잡도(Time Complexity) 분석

• 표현 척도
  - Input size(입력 크기)
  기준: 배열의 크기, 리스트의 길이, 행렬에서 행과 열의 크기, 트리에서 마디와 이음선의 수, 그래프에서는 정점과 간선의 수
  - Basic operation (단위연산)
  기준: 비교 (comparison), 지정 (assignment), 함수 호출 수(number of function calls)

  ⭐알고리즘을 분석 방법의 종류

• Every-case time complexity analysis (모든 경우 분석)
  • T(n) – the number of times the algorithm does the basic operation
    for an instance of size n
• Worst-case time complexity analysis (최악의 경우 분석)
  • W(n) – the maximum number of times the algorithm will ever do
    its basic operation for an input size of n
• Average-case time complexity analysis (평균의 경우 분석)
  • A(n) - the average number of times the algorithm does
    the basic operation for an input size of n
• Best-case time complexity analysis (최선의 경우 분석 )
  • B(n) – the minimum number of times the algorithm will ever do
    its basic operation for an input size of n

⭐ 차수(Order) - 자세한 식은 자료구조 개요

1. $O$

• Big O, asymptotic upper bound (n이 무한으로 갈때 상한범위)

2. $\Omega$

• Omega, asymptotic lower bound (n이 무한으로 갈때 하한범위)

2. $\theta$

• Theta, order, asymptotic tight bound (n이 무한으로 갈때 $O$와 $\Omega$의 교집합)

• $\theta$ (lg n) < $\theta$ (n) < $\theta$ (n * lg n) < $\theta$ ($n^2$)<$\theta$ ($n^j$) < $\theta$ ($n^k$) < $\theta$ ($a^n$) <
  $\theta$ ($b^n$) < $\theta$ ($n!$)
  • 여기서 k>j>2이고 b>a>1이다.

⭐ 극한(limit)를 이용하여 차수를 구하는 방법

Ex) 예시