[알고리즘] Branch-and-Bound

⭐Branch-and-Bound란?.

분기 한정법(分岐限定法, Branch and bound) 은 다양한 최적화 문제를 풀기 위한 범용 알고리즘이다. 분기 한정법은 모든 후보해를 체계적으로 늘어놓으면서 최적화할 수치의 상한과 하한을 추정, 가망 없다는 판정이 나는 해를 제거해 나간다. 제거하는 해에서 파생되는 해는 살펴보지 않기 때문에 불필요한 시간 소모를 줄이게 된다.

정리하자면 , 가능성(가능성 판단 척도=Bound)을 판단하여 가망이 없다면 더 이상 진행하지 않고 돌아간다.

⭐Backtracking과 Branch-and-Bound

• 유사한점
  • 상태 공간 트리를 기반으로 한다.
• 다른점
  • Backtracking: 가보고 더 이상 진행이 되지 않으면 돌아온다.
  • Branch&Bound: 최적해를 찾을 가능성이 없으면 분기를 하지 않는다.
    또한 Backtracking과 달리 최적화 문제를 푸는데만 사용한다.

⭐Branch-and-Bound 설계 전략

Bound라는 변수를 계산한다.
이때 Bound는 이후 발생할 최적의 값을 예측하는 것이다. 이 최적의 값이 best로 기록된 solution보다 안 좋을 시 분기를 하지 않는다.

⭐Breadth-First Search(너비 우선 탐색)

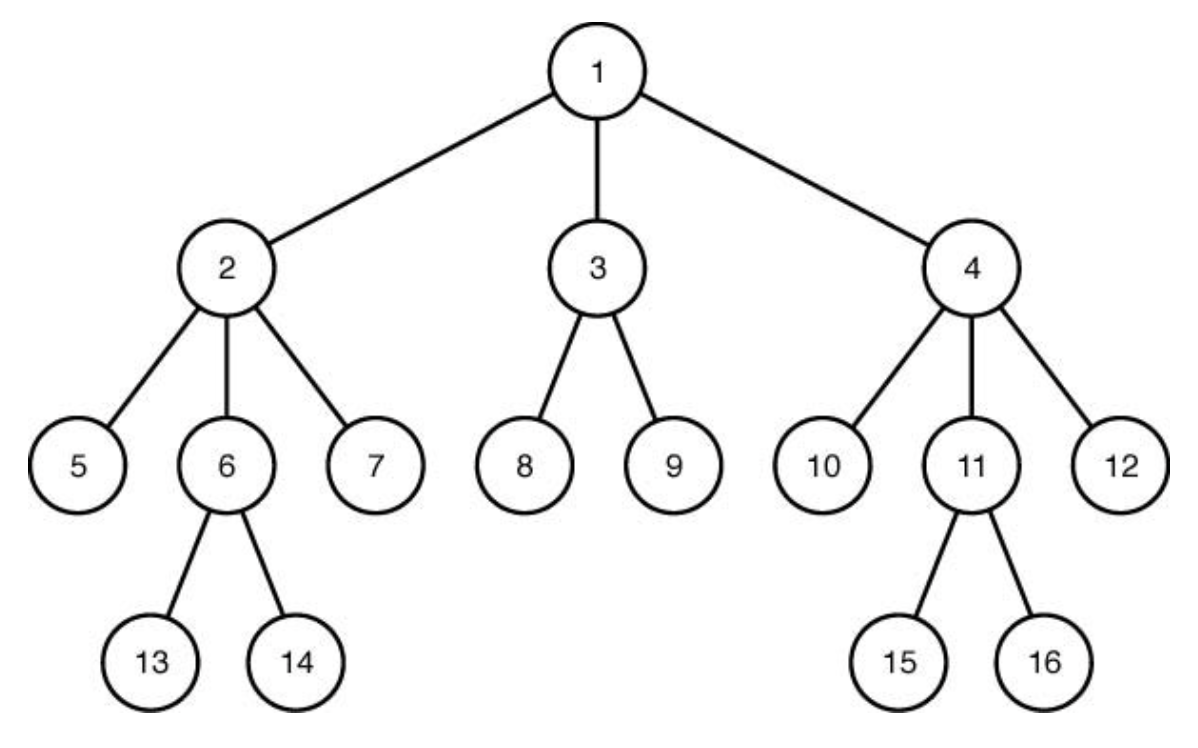
같은 레벨부터 차례대로 다 탐색하는 기법(Queue를 사용한다.)
1->
2-> 3-> 4->
5-> 6-> 7-> 8-> 9-> 10-> 11-> 12->
13-> 14-> 15-> 16

 void breadth_first_search(tree T) {
    queue_of_node Q;
	node u, v;
	initialize(Q);       // Initialize Q to be empty
	v = root of T;
	visit v;
	enqueue(Q,v);
	while(!empty(Q)) {
       dequeue(Q,v);
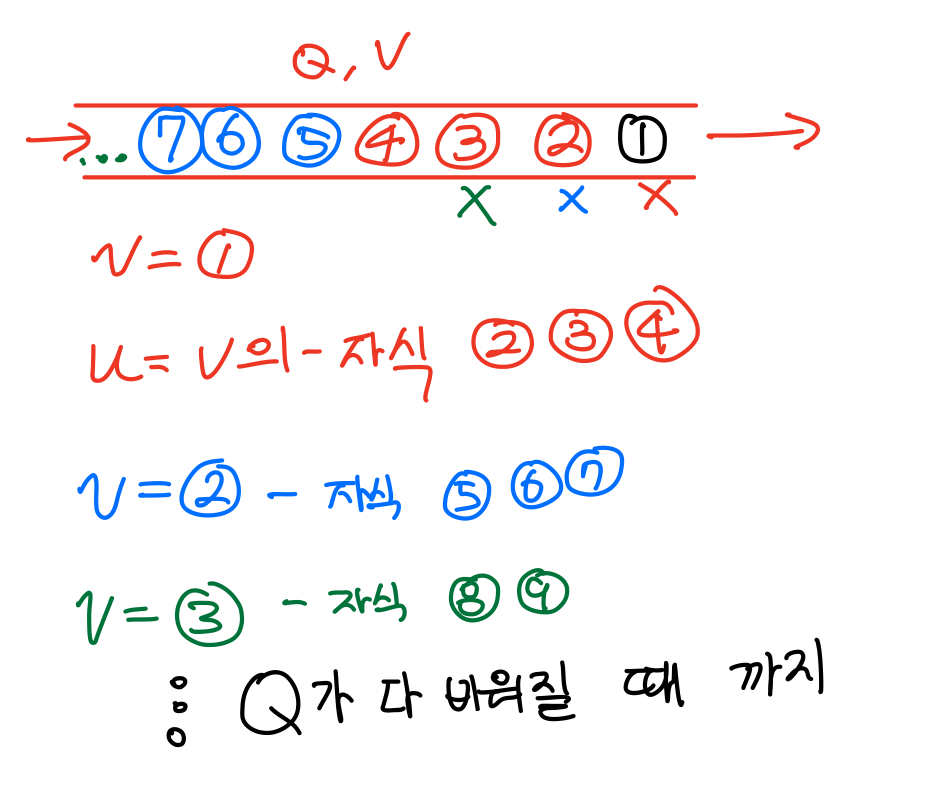
       for(each child u of v) {
		  visit u;
          enqueue(Q,u);
       }
	} 
}

⭐ 0-1 Knapsack Problem - Breadth-First Search + Branch-and-Bound(분기 한정법)

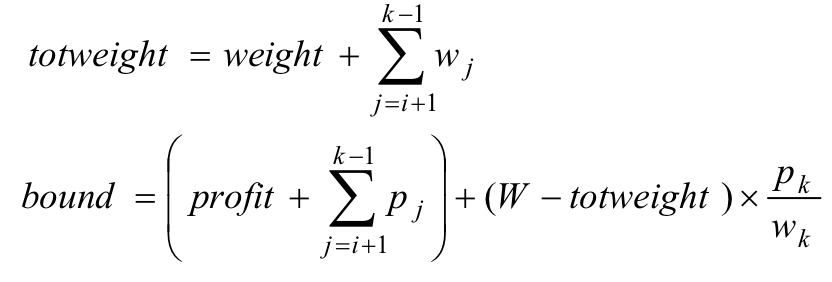
bound 계산법
bound= 현재 가치 + 넣을 수 있는 최대 가치의 item들 + 무게별 가치가 높은 아이템 중 안 넣은 아이템을 fractional(가루형태)로 넣을 경우

• 여기서 가루 형태는 한 물체를 쪼갤 수 있다고 생각하면 쉽다.

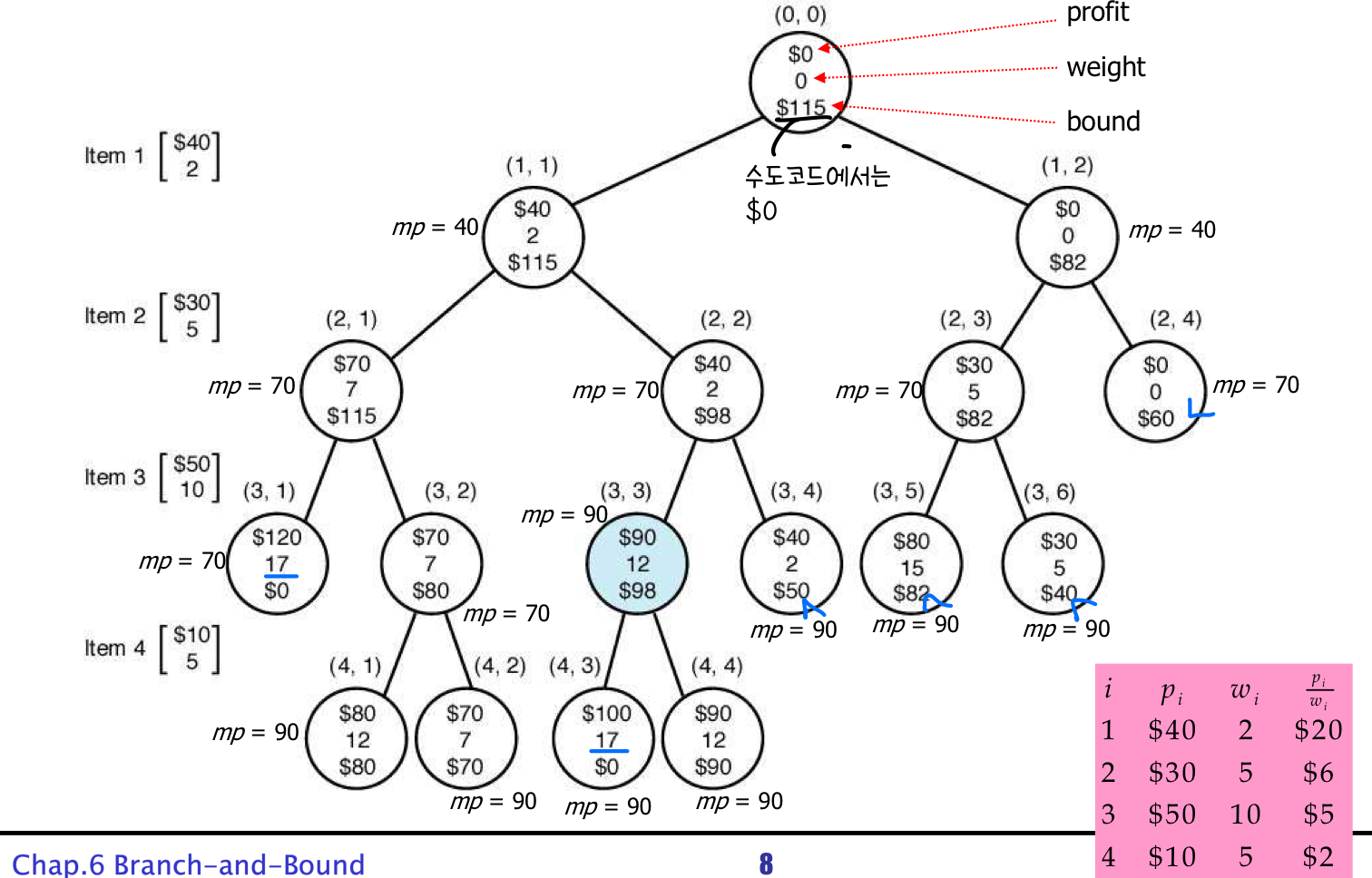
코드

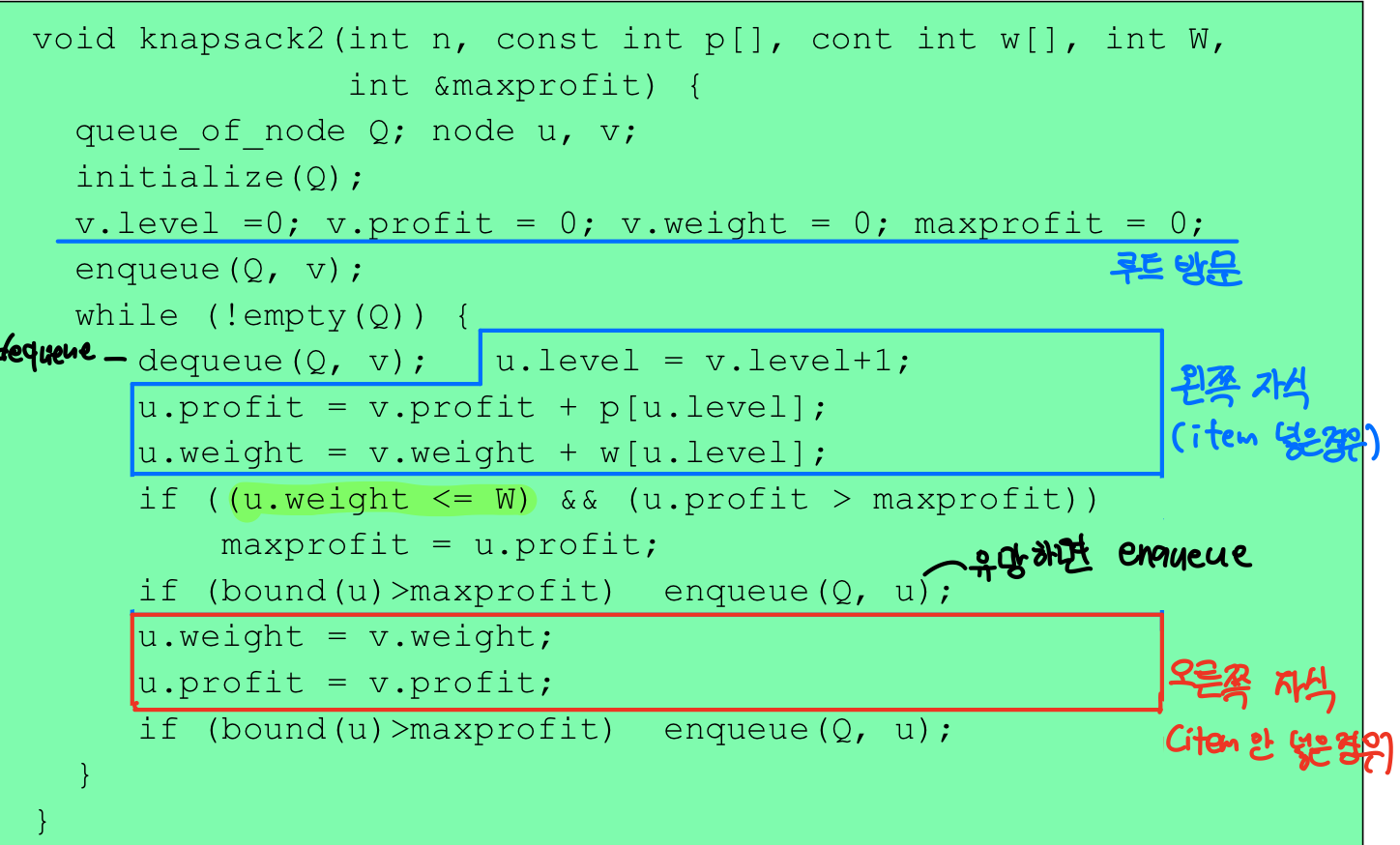
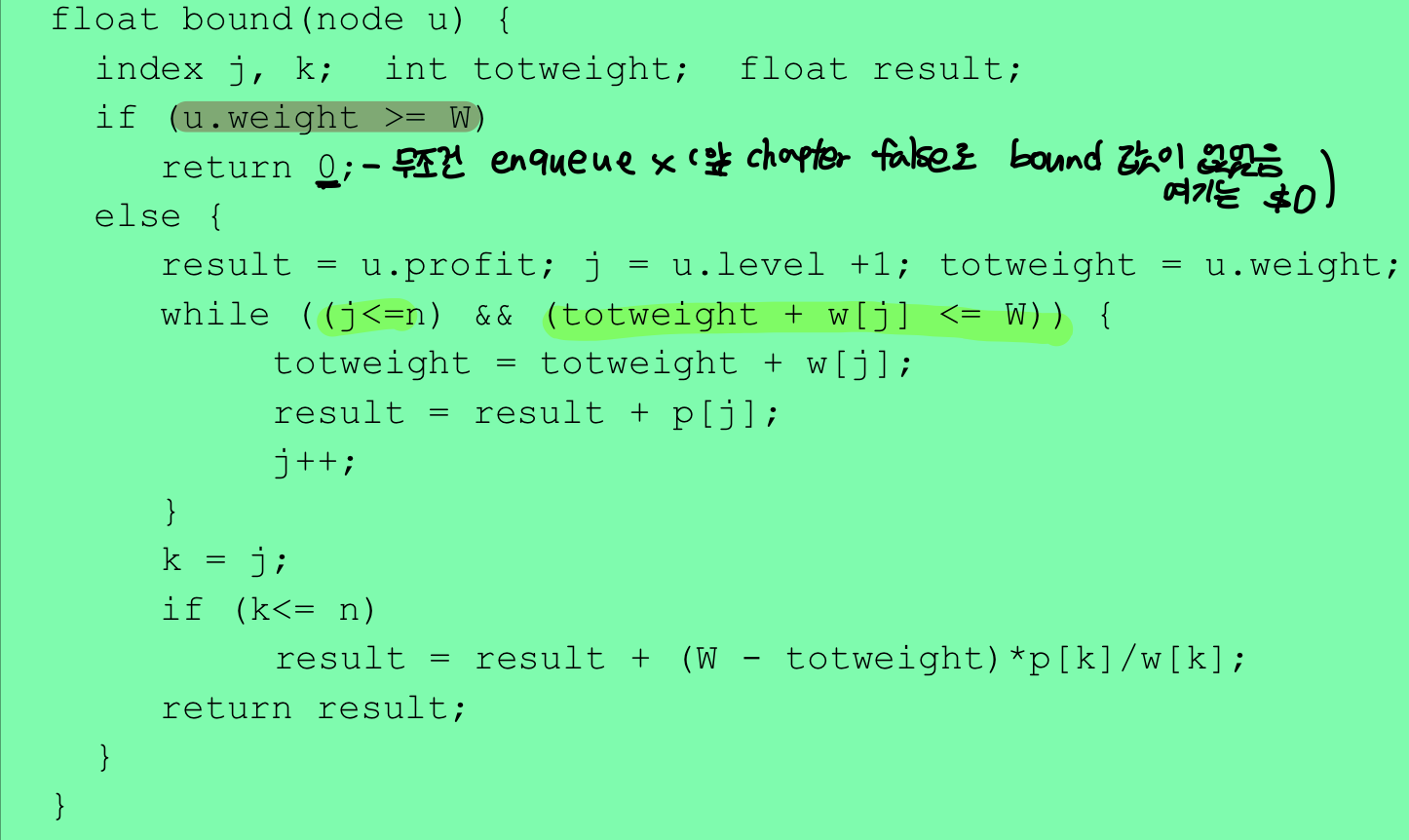
⭐ 0-1 Knapsack Problem - Best-First Search

Best-First Search의 전략

• 우선순위 큐(Priority Queue) 사용

우선 순위의 기준 - Bound

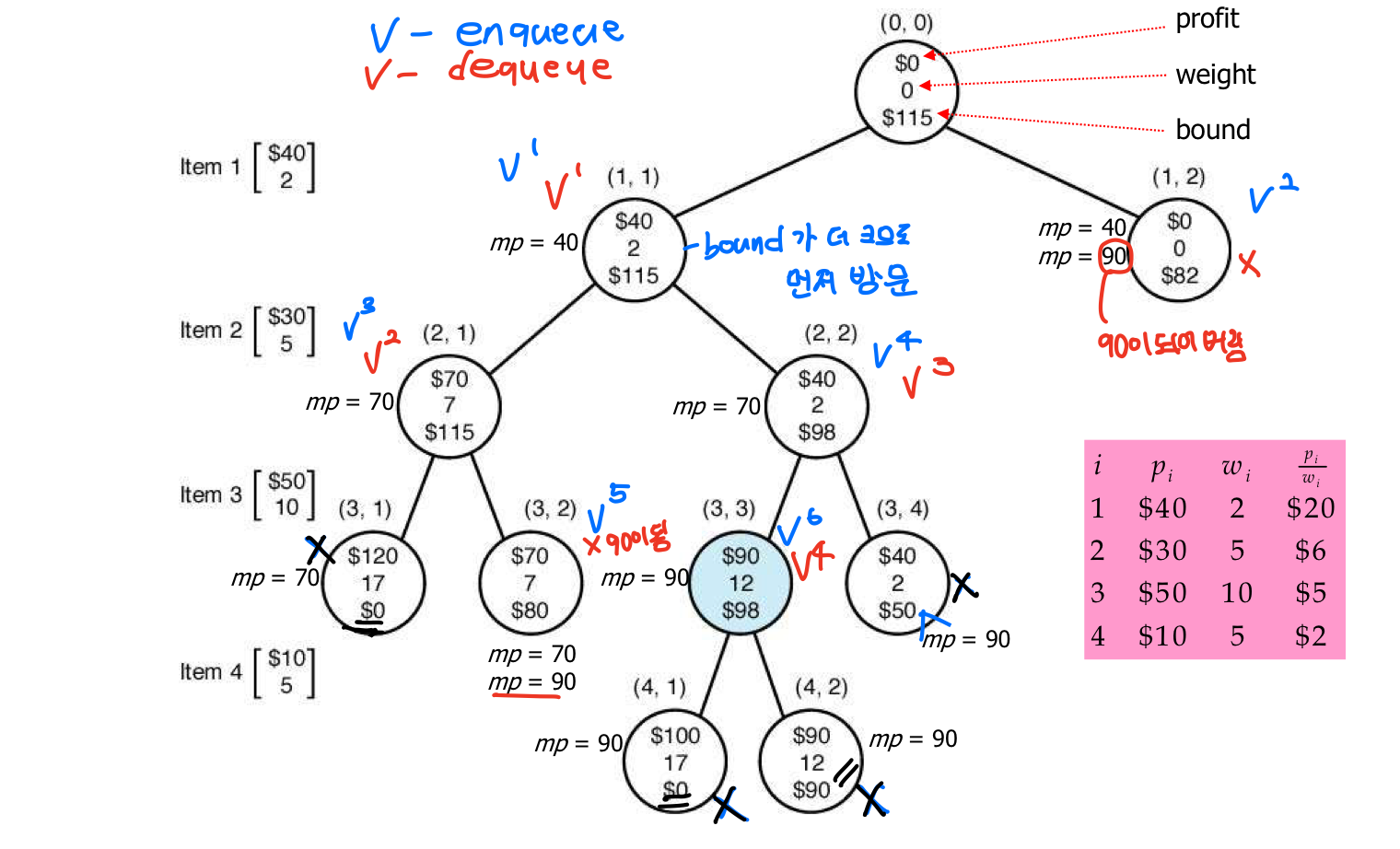
dequeue시에도 유망한지 체크하여 넣을 때에는 유망했는데 나올 때에는 유망하지 않을 수 있다.
dequeue는 가장 유망한 것부터 먼저 한다.

• 유망하다는 것은 bound가 크다는 것이다.

가장 유망하더라도 더 안 유망한 것이 크게 나올 수 있기 때문에 유망한 경우에는 다 탐색을 해보아야한다.

 void knapsack3(int n, const int p[], cont int w[], int W, int &maxprofit){
     queue_of_node  PQ;  node u, v;
     initialize(PQ);
     v.level =0;  v.profit = 0;  v.weight = 0;  v.bound = bound(v);
     maxprofit = 0;
     insert (PQ, v);
	 while (!empty(PQ)) { // Remove nod with 
     	remove(PQ, v); // best bound 
        if(v.bound > maxprofit) { // Check if node is still
			u.level = v.level+1; // promising. 
            u.profit = v.profit + p[u.level]; 
            u.weight = v.weight + w[u.level];
       		if ((u.weight <= W) && (u.profit > maxprofit))
          		 maxprofit = u.profit;
                 
       		u.weight = v.weight; // Set u to the child
			u.profit = v.profit; //that does not include
			u.bound = bound(u);  //the next item
       		if (bound(u) > maxprofit) insert (PQ, u);
		} 
    }
}

⭐ The Traveling Salesperson Problem - 외판원 문제

출발점에서 모든 노드를 다 방문하고 다시 출발점으로 돌아오는 문제

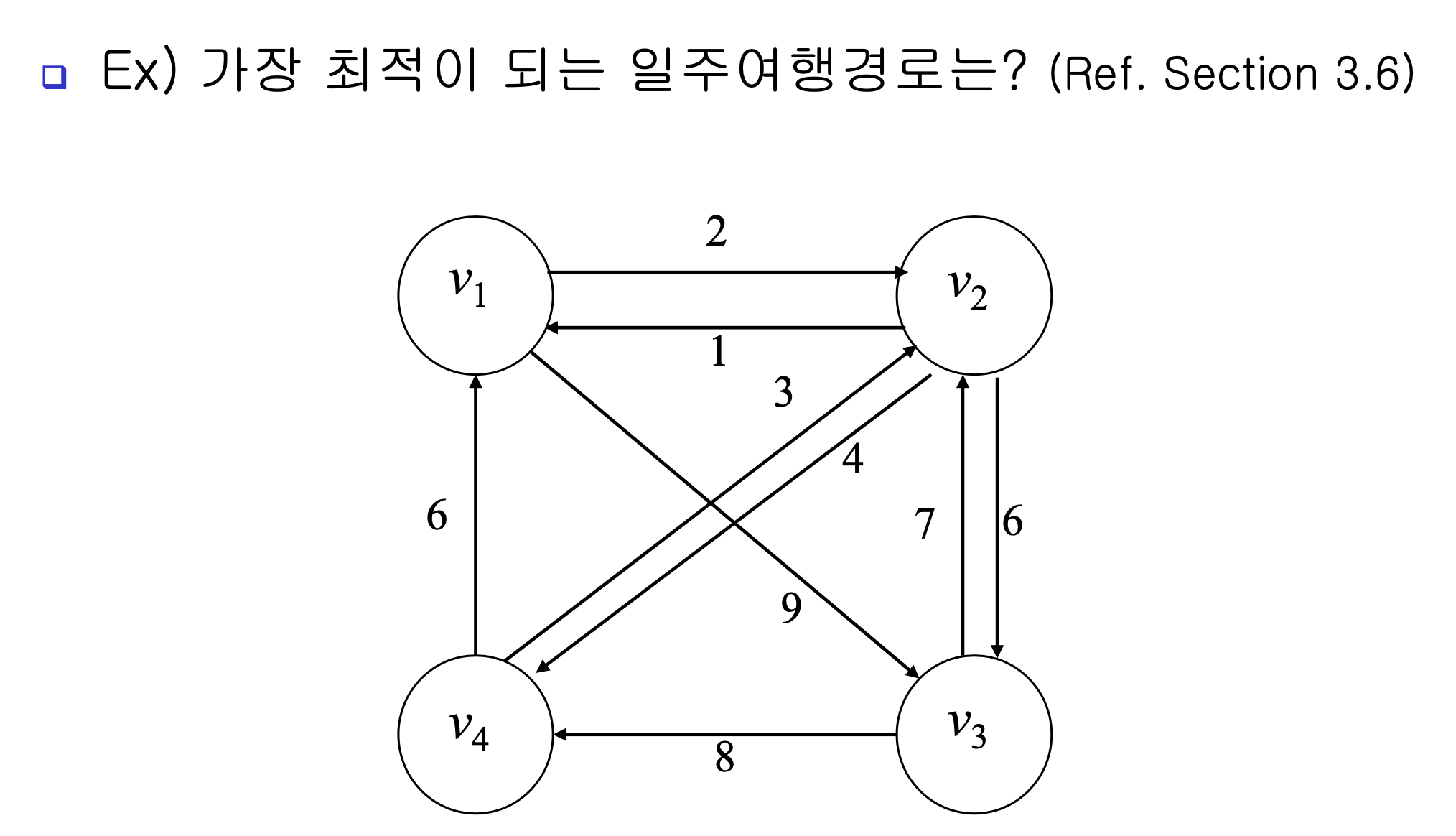
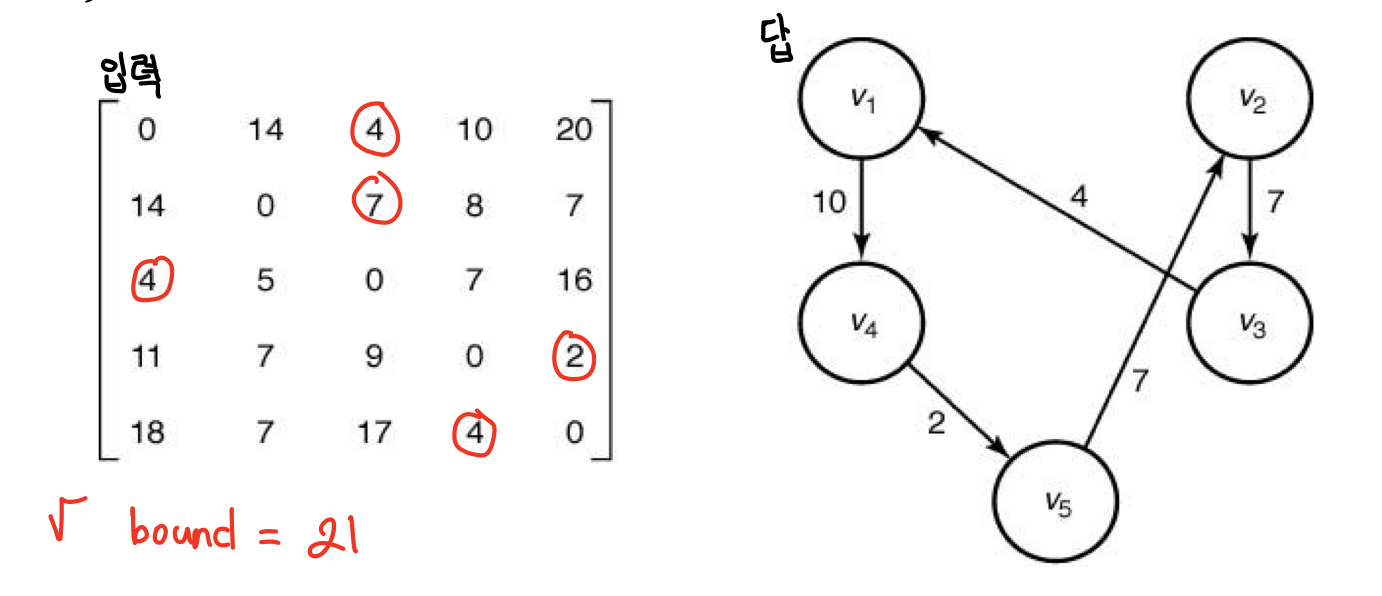
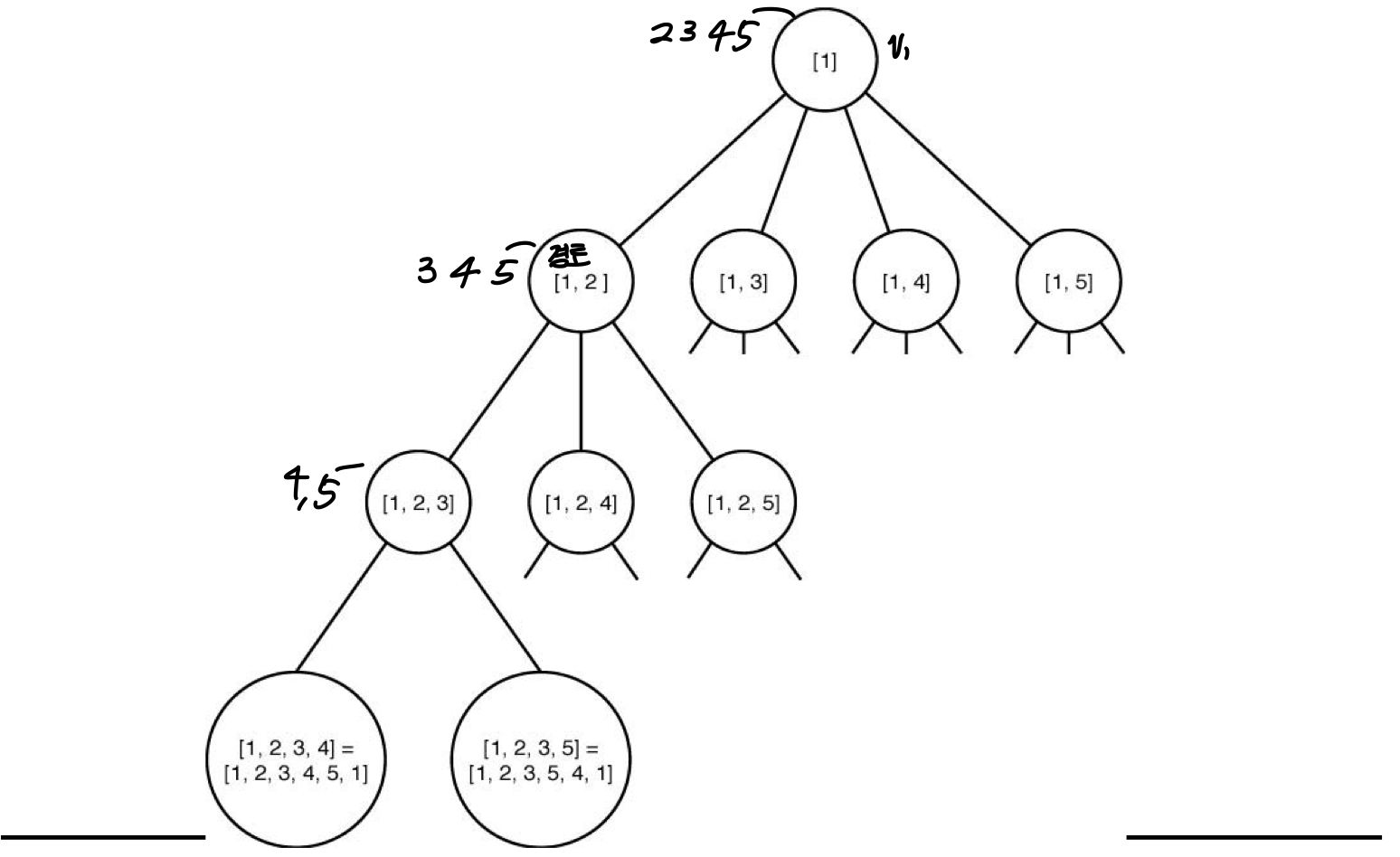
⭐Bound(lower bound) 계산법

결과적으로 $v_1, v_2, v_3, v_4, v_5$ 모두 한 번씩 들려서 어딘가로 나가야한다.
이 때 최선의 경우로 노드들을 들려서 나간다고 가정한다.

첫 경로의 bound는 모든 노드에서 출발하여 가장 작은 경로로 갈 수 있는 노드를 골라 가중치를 다 더한다.

두번째 경로부터는
이미 지나온 경로의 가중치 + {안 고른 노드 + 현재 노드} 에서 각 노드가 어딘가로 나가는 간선의 경우의 수 중 작은 것을 골라 가중치를 합하면 된다.

단 규칙이 있는데,

규칙 1. 이미 방문한 노드로의 경로 는 빼야 한다.
여기서 v1 노드(출발지)는 제외해야 한다, 이유는 도착지로 v1을 한 번 더 방문해야하기 때문이다.

규칙 2.현재 노드에서 간선을 선택할 때에는 $v_1$으로 가는 경우도 빼야한다.
이유는 현재에서 바로 $v_1$으로 간다면 도착지를 바로 다른 노드 방문없이 가게되는 것이기 때문이다.

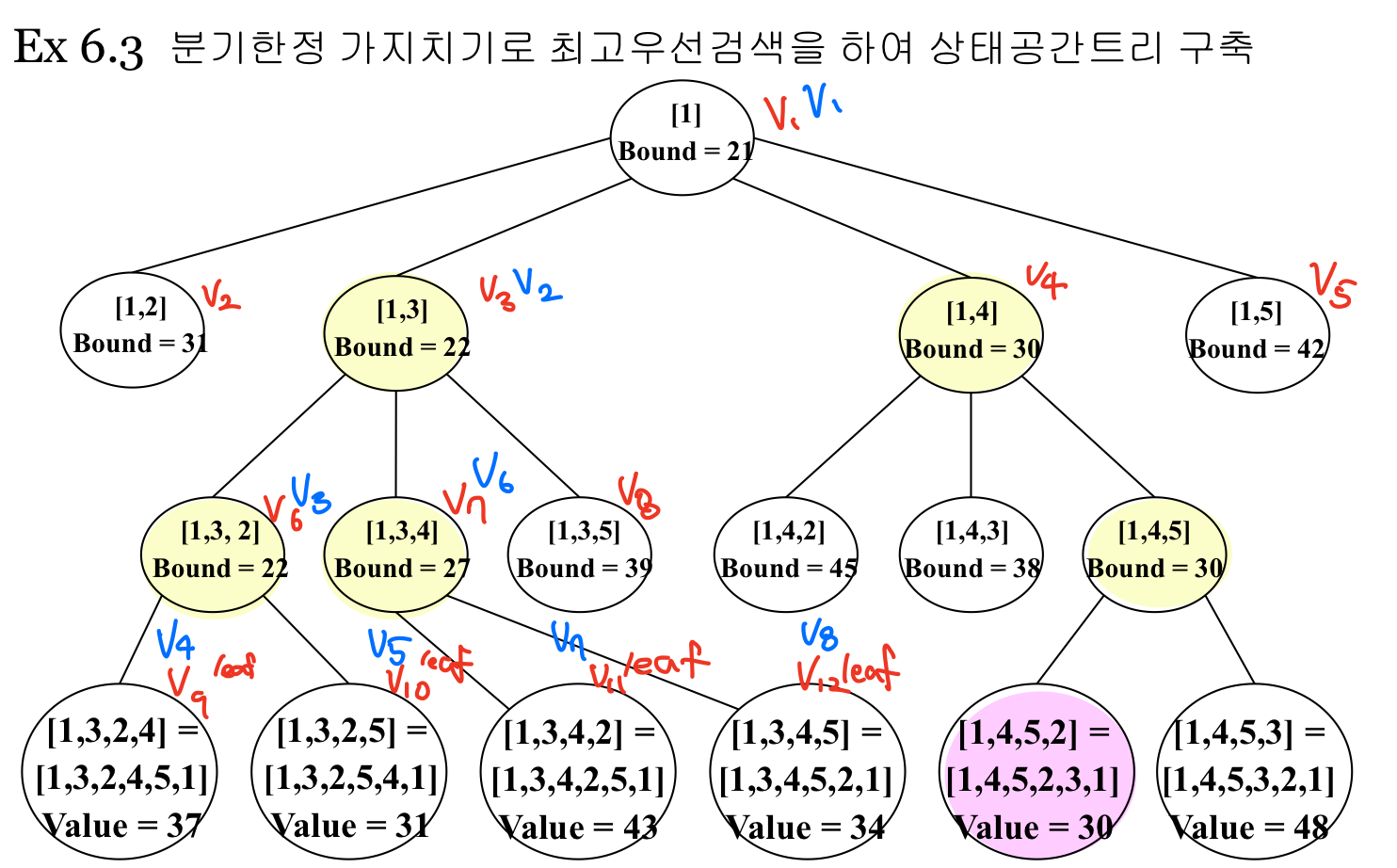
 void  travel2(int n, const number W[][], ordered_set &opttour, number &minlength) {
     priority_queue_of_node PQ;
     node u, v;
     
     initialize(PQ);
     v.level =0;
     v.path = [1];
     v.bound = bound(v);
     minlength = INFINITE;
     insert(PQ, v);
     while (!empty(PQ)) {
 		 remove(PQ, v);
  		if (v.bound < minlength) {
    		u.level = v.level + 1;
    		for ((all i such that 2< i< n) && (i is not in v.path)) {
       			u.path = v.path;
       			put i at the end of u.path;
       			if (u.level == n-2) {
          			put index of only vertex
          			not in u.path at the end of u.path;
          			put 1 at the end of u.path;
          			if (length(u)<minlength) {
              			minlength = length(u);
              			opttour = u.path;
					}
             	}
       			else {
          			u.bound = bound(u);
          			if (u.bound < minlength) insert(PQ, u);
 		        } 
            } //for close
      } //if close
   } //while close
}

⭐ 요약

Branch and Bound (분기 한정법) 알고리즘 완전 정리

Branch and Bound(분기 한정법)은 최적화 문제(예: 외판원 문제, 0-1 배낭 문제 등)를 해결하기 위한 탐색 기법으로, 상태 공간 트리를 기반으로 합니다.
모든 해를 전부 탐색하지 않고, 가능성이 없는 분기(branch)는 bound(상한/하한) 계산을 통해 가지치기하여 탐색 효율을 높입니다.

---

주요 내용 요약

1️⃣ Branch and Bound 개념

• 가능한 해를 체계적으로 나열하며, 가망 없는 해는 제거
• 최적화 문제 해결에 사용됨

---

2️⃣ Backtracking과의 차이점

비교 항목	Backtracking	Branch and Bound
트리 기반	✅	✅
언제 되돌아감	조건 만족 X	최적해 가능성 X
사용 목적	해 찾기	최적해 찾기

---

3️⃣ Knapsack 문제 예제

• Breadth-First Search: 너비 우선 탐색 방식으로 노드를 전개
• Best-First Search: Bound 기준으로 우선순위 큐 사용
  → 둘 다 bound 계산이 핵심!

---

4️⃣ 외판원 문제 (TSP) 적용

• 각 노드에서 가장 작은 간선을 선택하여 bound 계산
• 규칙 1️⃣: 지나온 노드 제외
• 규칙 2️⃣: 현재 노드에서 바로 출발지로 가는 간선 제외

---

🎯 핵심 포인트

• Bound 계산이 핵심 로직
• 상태 공간 트리를 효율적으로 잘라내는 전략
• 실전 문제 적용:
  • 0-1 배낭 문제
  • 외판원 문제 (TSP)

---