⭐Backtracking이란?
모든 경우의 수를 전부 고려하는 알고리즘. 상태공간을 트리로 나타낼 수 있을 때 적합한 방식이다. 일종의 트리 탐색 알고리즘이라고 봐도 된다. 방식에 따라서 깊이우선탐색(Depth First Search, DFS)과 너비우선탐색(Breadth First Search, BFS), 최선 우선 탐색(Best First Search/Heuristic Search)이 있다. 그냥 뇌없이 짤 수 있다는 것이 장점이다.
⭐Depth-First Search (깊이 우선 검색)
트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식이다. 대표적으로 백트래킹에 사용한다. 일반적으로 재귀호출을 사용하여 구현하지만, 단순한 스택 배열로 구현하기도 한다. 구조상 스택 오버플로우를 유의해야 한다.[
void depth_first_tree_search (node v) {
node u;
visit v;
for (each child u of v)
depth_first_tree_search(u)
}
⭐N-Queens Problem
- 4(=n)개의 Queen을 서로 상대방을 위협하지 않도록
4 x 4 서양장기(chess)판에 위치시키는 문제이다. - 서로 상대방을 위협하지 않기 위해서는 같은 행이나,
같은 열이나, 같은 대각선 상에 위치하지 않아야 한다.
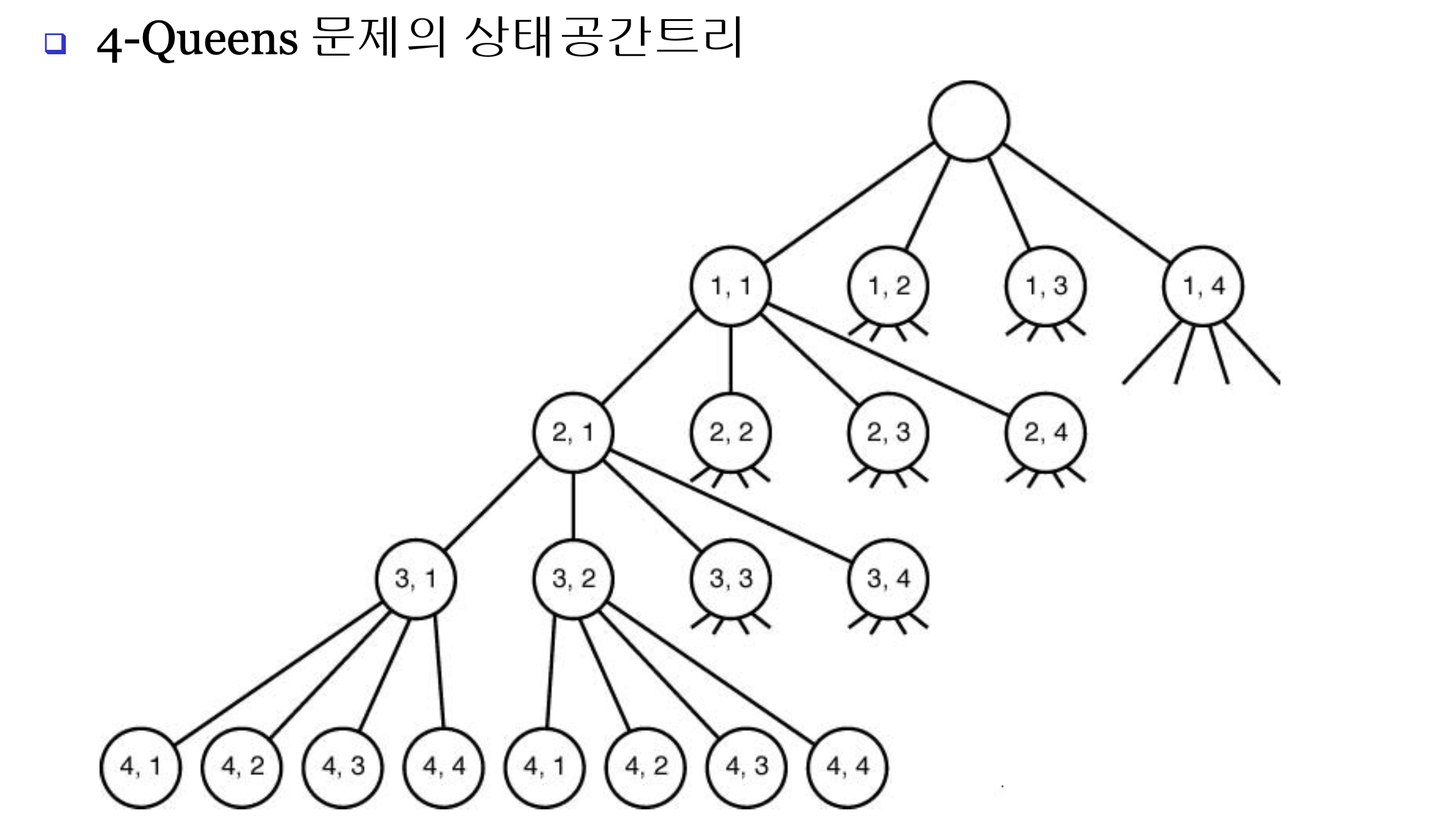
같은 level의 노드는 같은 행을 의미한다.
void checknode (node v) {
node u;
if (promising(v))
if (there is a solution at v)
write the solution;
else
for (each child u of v)
checknode(u);
}
N-Queens에서 Promising 여부 판단식
- 같은 열인 경우 non promising
- If (col(i) == col(k)) nonpromising;
- 대각선인 경우 non promising
- If (abs(col(i) - col(k)) == abs(i - k)) nonpromising;
N-Queens pseudo code
void queens (index i) {
index j;
if (promising (i))
if (i == n) cout << col[1] through col[n];
else
for (j=1; j<=n; j++) {
col[i+1] = j;
queens(i+1);
}
}
bool promising (index i) {
index k;
bool switch;
k = 1;
switch = TRUE;
while (k<i && switch) {
if (col[i]==col[k] || abs(col[i]–col[k])==abs(i-k))
switch = FALSE;
k++
}
return switch;
}N-Queens같은 경우는 알고리즘의 복잡도를 정확하게 얘기하기가 애매하다.
이유:
- 대각선을 점검하는 경우를 고려하지 않았다.
따라서 실제 유망한 노드의 수는 훨씬 더 작을 수 있다.- 유망하지 않은 노드를 포함하고 있는데, 실제로 해석의 결과에 포함된 노드 중에서 유망하지 않은 노드가 훨씬 더 많을 수 있다.
이러한 이유로 Monte Carlo 기법을 사용한다.
⭐A Monte Carlo Algorithm
몬테카를로 알고리즘이란?
몬테카를로 방법 은 반복된 무작위 추출을 이용하여 함수의 값을 수리적으로 근사하는 알고리즘을 부르는 용어이다.
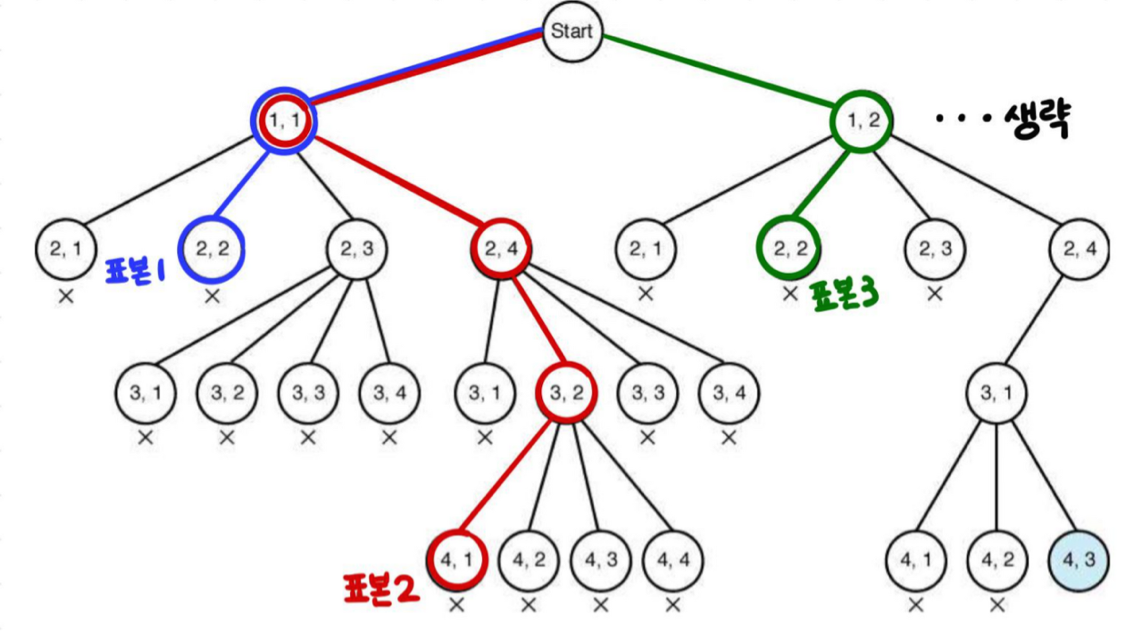
Monte Carlo 기법을 사용한 백트랙킹 알고리즘의 수행시간 추정방법
-
뿌리노드의 유망한 자식노드의 개수를 이라고 한다.
-
상태공간트리의 수준 1에서 유망한 노드 하나를 무작위로 정하고,
그 노드의 유망한 자식노드의 개수를 이라고 한다. -
위에서 정한 노드의 유망한 노드 하나를 다시 무작위로 정하고,
그 노드의 유망한 자식노드의 개수를 라고 한다. -
더 이상 유망한 자식노드가 없을 때까지 이 과정을 반복한다.
핵심 식


⭐Sum-of-subsets Problem

유망한지 판단 여부
total = 앞으로 더할 수 있는 최대치
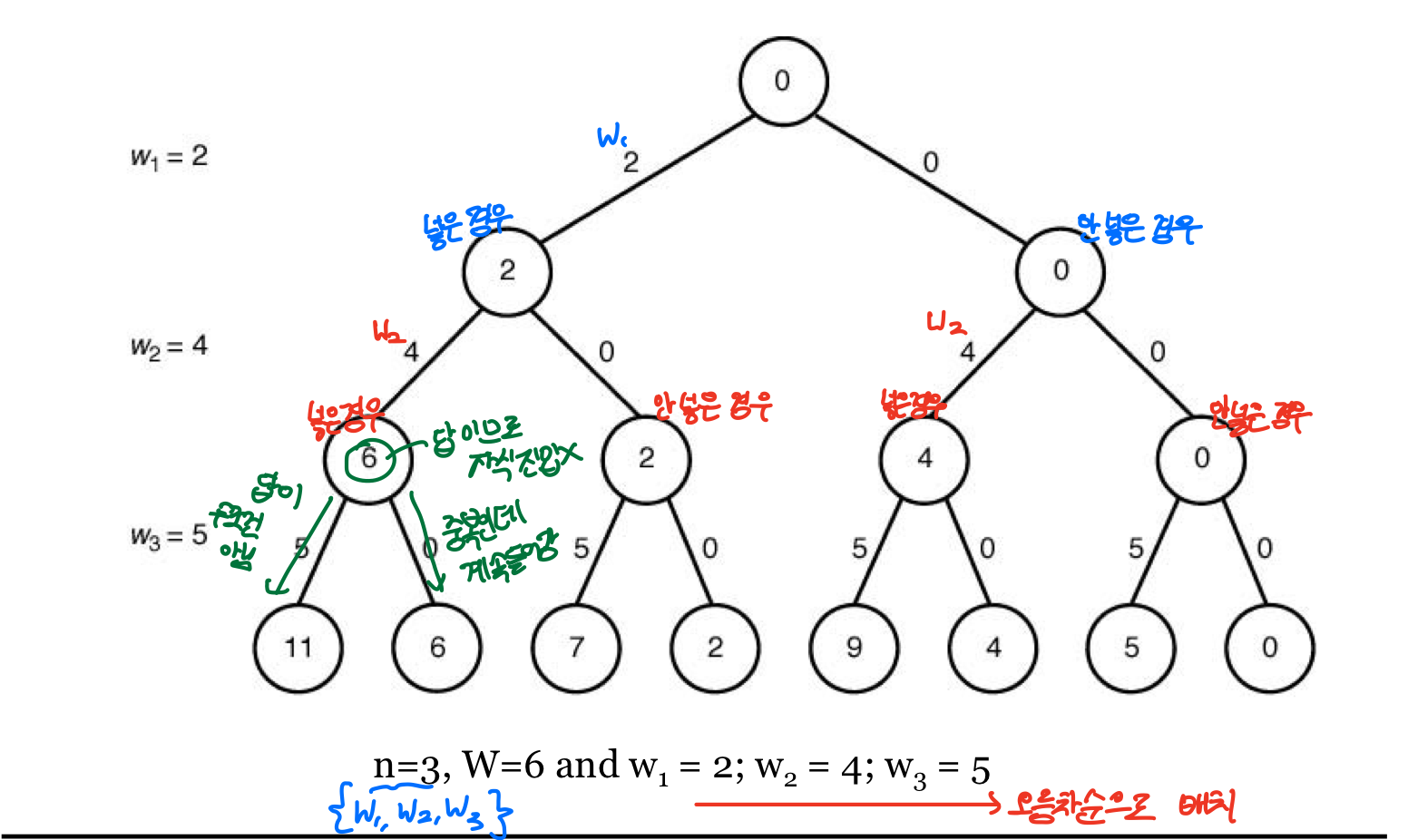
void sum_of_subsets (index i, int weight, int total) {
if (promising(i)) {
if (weight ==W)
cout << include[1] through include[i];
else {
include[i+1] = “yes”;
sum_of_subsets(i+1, weight+w[i+1], total-w[i+1]);
include[i+1] = “no”;
sum_of_subsets(i+1, weight, total-w[i+1]);
}
}
bool promising (index i) {
return (weight+total >= W)
&& (weight == W || weight+w[i+1] <= W);
}
시간 복잡도 W(n):
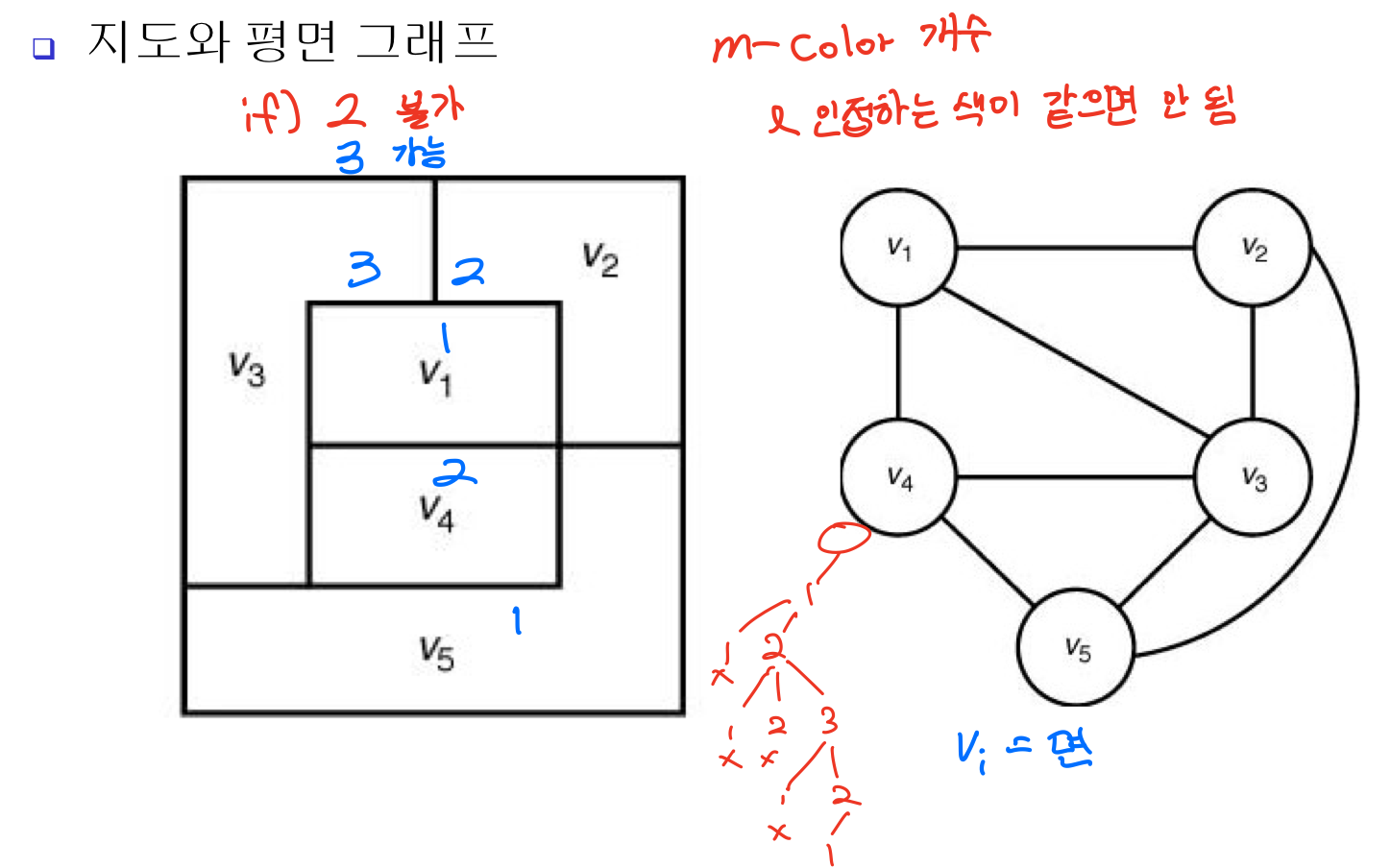
⭐Graph Coloring
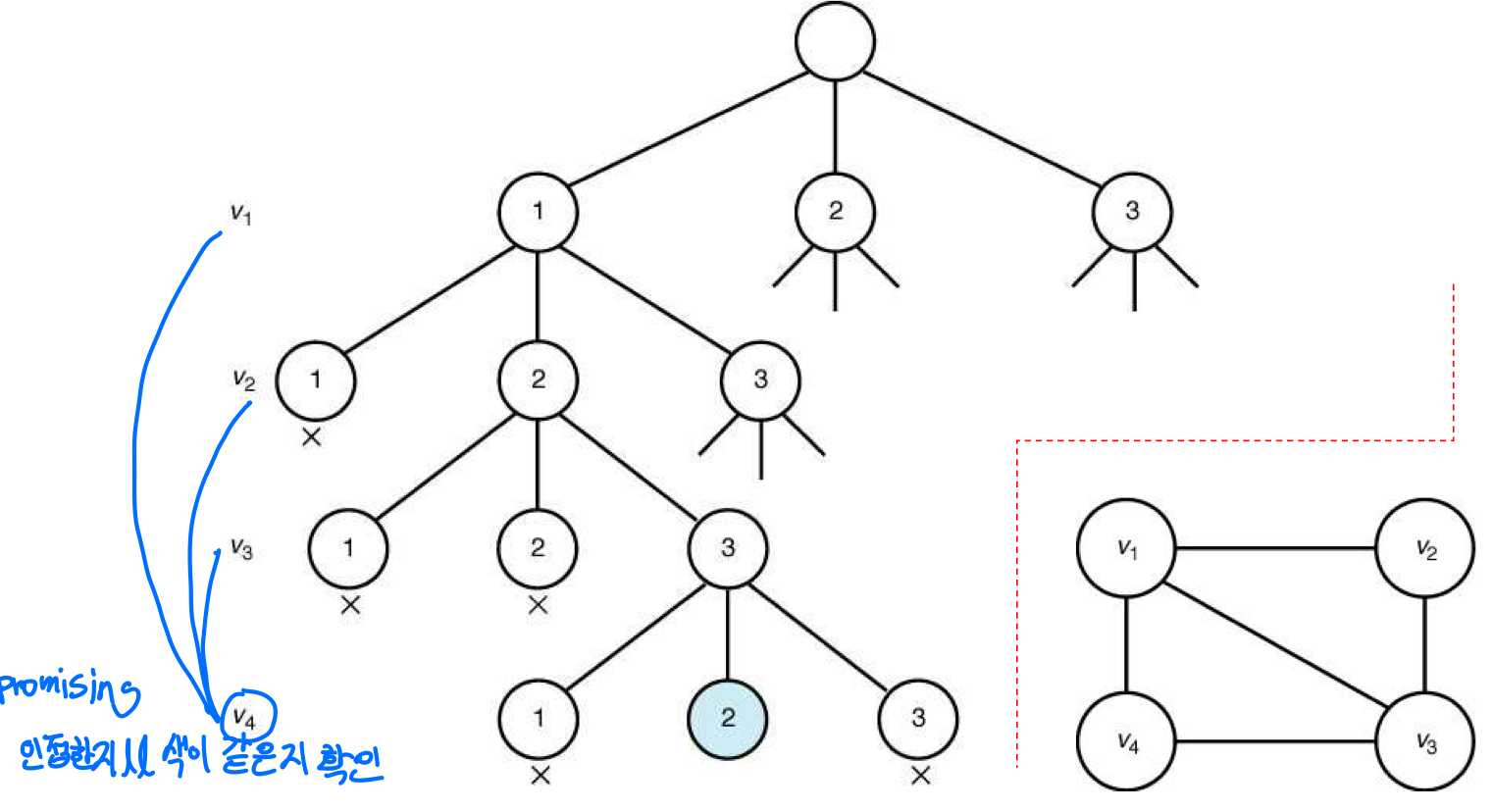
Graph Coloring Problem
- m-coloring – 지도에 m가지 색으로 색칠하는 문제
- m개의색을가지고,인접한지역이같은색이되지않도록지도에 색칠하는 문제
void m_coloring (index i) {
int color;
if (promising(i))
if (i == n) cout << vcolor[1] through vcolor[n];
else
for (color = 1; color<=m; color++) {
vcolor[i+1] = color;
m_coloring(i+1);
}
}
bool promising(index i) {
int j; bool switch;
switch = TRUE;
j = 1;
while (j<i && switch) {
if (W[i][j] && vcolor[i]==vcolor[j]) switch = FALSE;
j++;
}
return switch;
}시간 복잡도 W(n):
⭐The 0-1 Knapsack Problem
wi와 pi를 각각 i번째 아이템의 무게와 값어치라고 하면, pi/wi 의 값이 큰 것부터 내림차순으로 아이템을 정렬한다. (일종의 탐욕적인 방법이 되는 셈이지만, 알고리즘 자체는 탐욕적인 알고리즘은 아니다.)
• profit: 그 노드에 오기까지 넣었던 아이템 값어치의 합.
• weight: 그 노드에 오기까지 넣었던 아이템 무게의 합.
• bound(최대 이익): 노드가 수준 i에 있다고 하고, 수준 k에 있는 노드에서 총 무게가 W를 넘는다고 하자. 그러면, 다음과 같이 bound를 구할 수 있다.
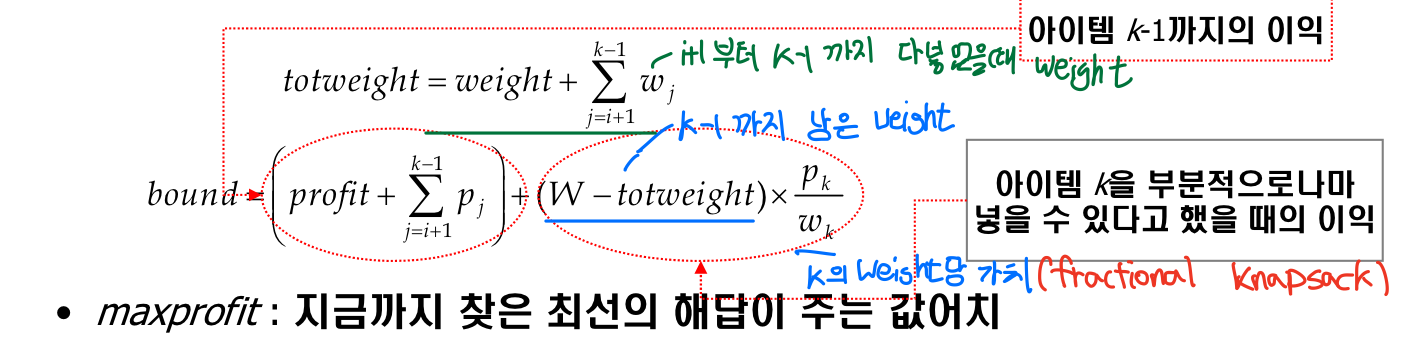
Promising 조건
(weight < W) and (bound > maxprofit)
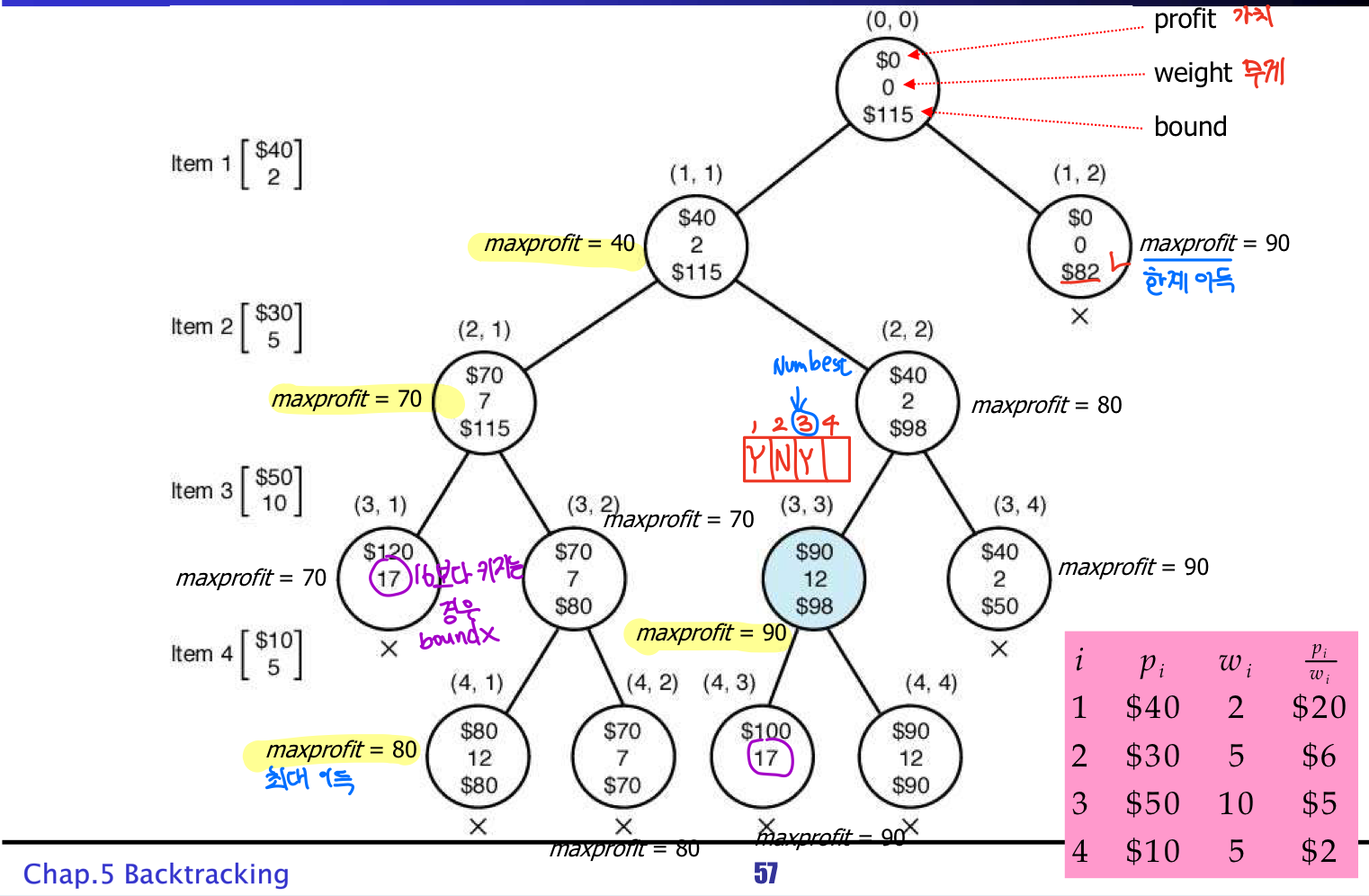
void knapsack (index i, int profit, int weight) {
if (weight <= W && profit > maxprofit) { // best so far
maxprofit = profit;
numbest = i;
bestset = include;
}
if (promising(i)) {
include[i+1] = “YES”; // Include w[i+1]
knapsack(i+1, profit+p[i+1], weight+w[i+1]);
include[i+1] = “NO”; // Not include w[i+1]
knapsack(i+1, profit, weight);
}
} bool promising(index i) {
index j, k;
int totweight;
float bound;
if (weight >= W) return FALSE;
else {
j = i+1;
bound = profit;
totweight = weight;
while ((j <= n) && (totweight +w[j] <= W)) {
totweight = totweight + w[j];
bound = bound + p[j];
j++
}
k=j;
if (k <= n)
bound = bound +(W–totweight)*p[k]/w[k];
return bound > maxprofit;
}
}시간 복잡도 W(n):


