There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
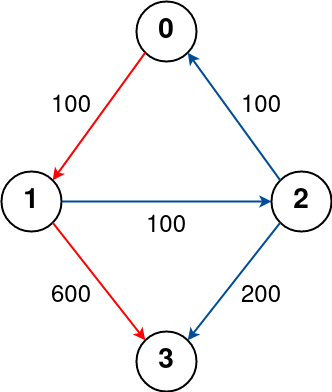
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
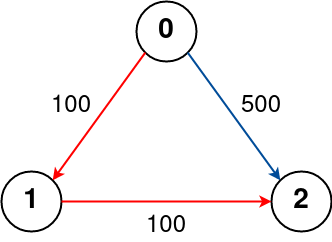
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
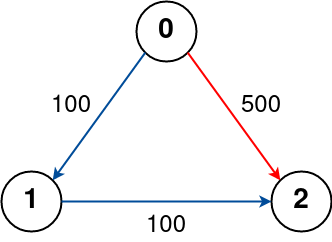
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= fromi, toi < n
fromi != toi
1 <= pricei <= 104
There will not be any multiple flights between two cities.
0 <= src, dst, k < n
src != dst
풀이
다익스트라 알고리즘 방식의 힙의 최대값 최소값을 구하는 방법으로 문제를 해결하였다.
다른 문제와 다르게 이 문제에서는 거칠수 있는 횟수가 k번으로 제한이 되어있었다는 점에서
k가 0보다 작을때 while문을 끝낸다는 조건으로 1번 반복 될때마다 k-1하는 방법으로 문제를 해결하였다.
class Solution(object):
def findCheapestPrice(self, n, flights, src, dst, k):
"""
:type n: int
:type flights: List[List[int]]
:type src: int
:type dst: int
:type k: int
:rtype: int
"""
graph = collections.defaultdict(list)
for f, t, p in flights:
graph[f].append((t, p))
q = [(0, src, k)]
result = collections.defaultdict(int)
while q:
price, node, K = heapq.heappop(q)
if node == dst:
return price
if K >= 0:
for v, w in graph[node]:
alt = price + w
heapq.heappush(q,(alt, v, K-1))
return -1