항해99 TIL 3주차 - 16

오늘은 최단경로를 구하는 알고리즘으로 다익스트라와 플로이드가 있는데
그 중에 다익스트라에 대해 학습했다.

다익스트라 알고리즘

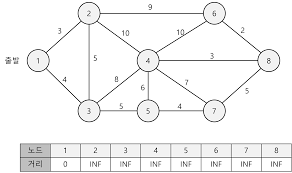
다익스트라 알고리즘이란 그래프의 한 정점에서 모든 정점까지의 최단경로를 구할때 사용되는 알고리즘이다.

다익스트라 알고리즘 시간복잡도

다익스트라 알고리즘의 시간복잡도는 O(N^2)의 시간복잡도를 가지지만
힙을 이용한 우선순위 큐를 사용하면 O((N+E)logN)의 개선된 시간복잡도를 가지게된다.

다익스트라 알고리즘 설명

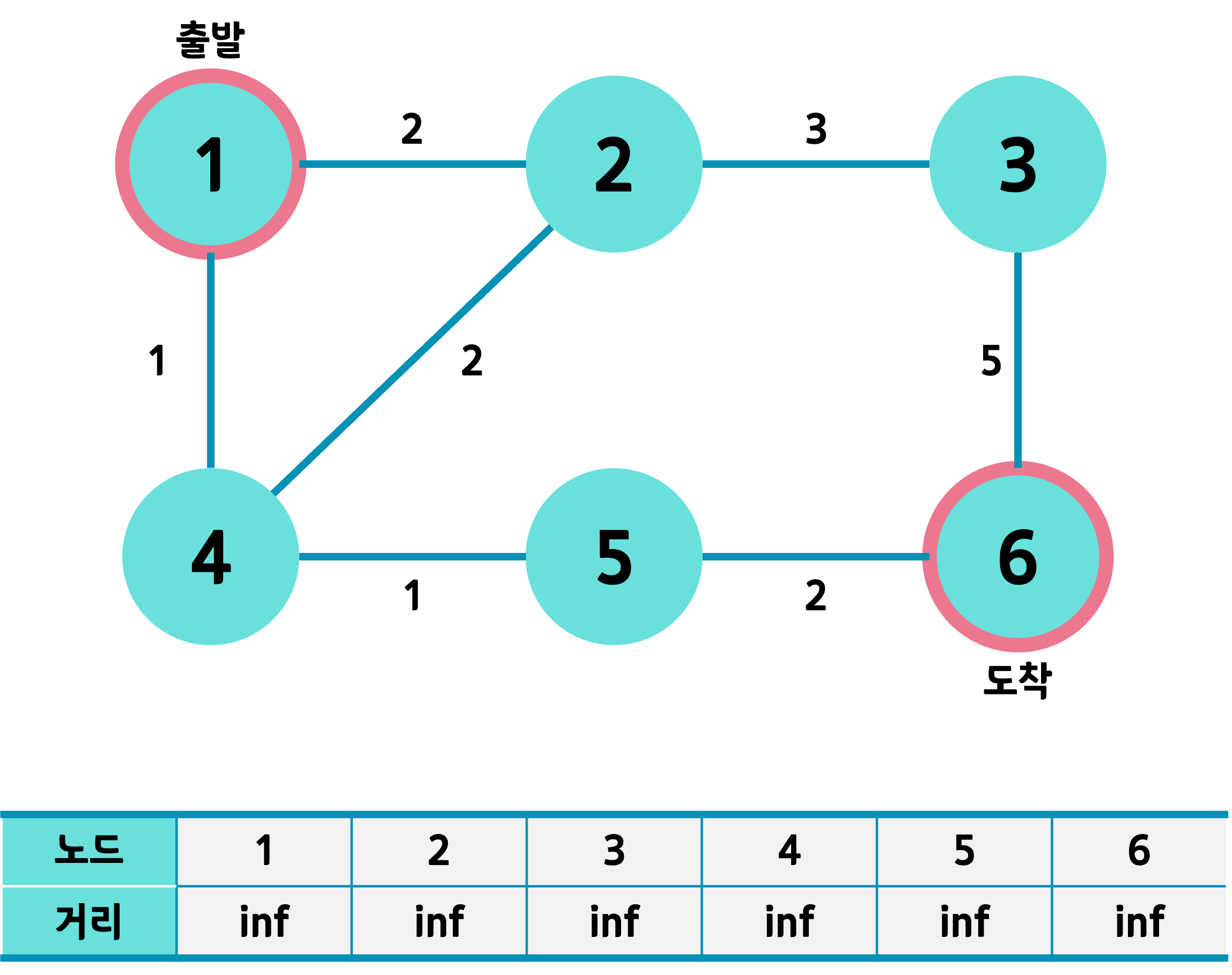
1번은 출발노드, 6번은 도착노드로 설정하였다

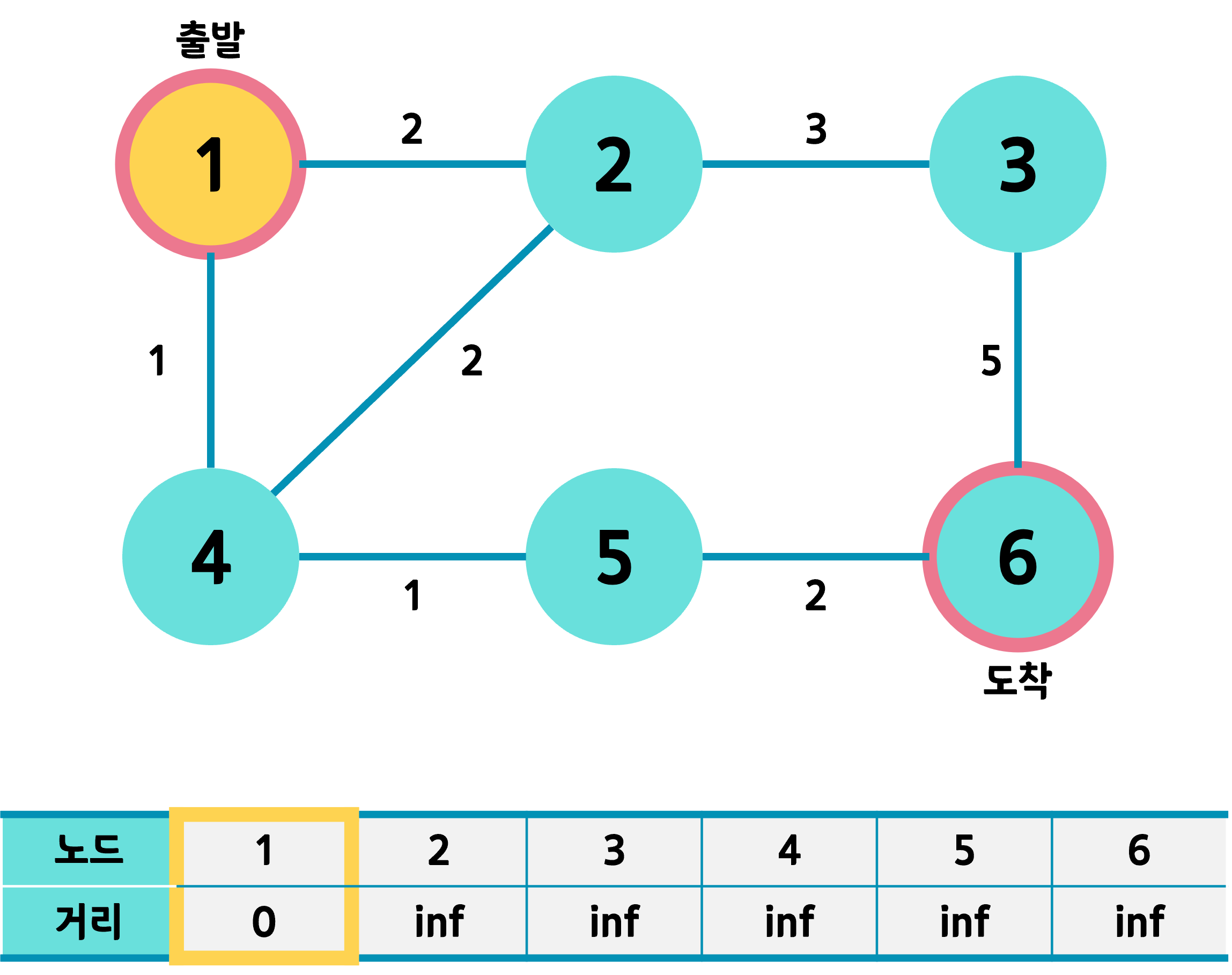
출발노드를 먼저 선택하고 거리를 0으로 바꾼다

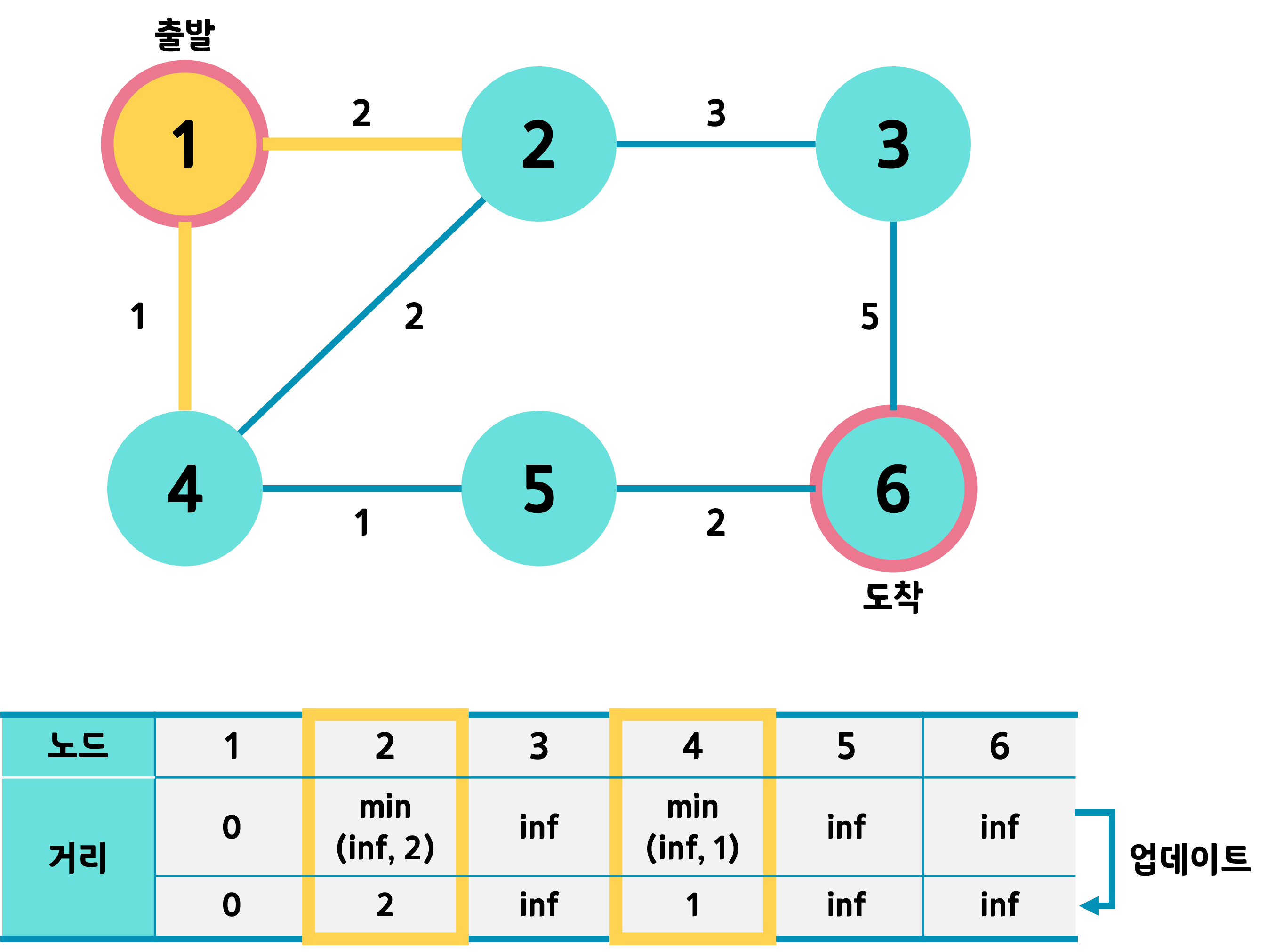
1번노드에서 갈 수 있는 방향은 2번노드와 4번노드이다. 2번노드는 거리가 2고 4는 1이다 각각의 거리를 저장하고 거리가 더 짧은 4로 이동한다.

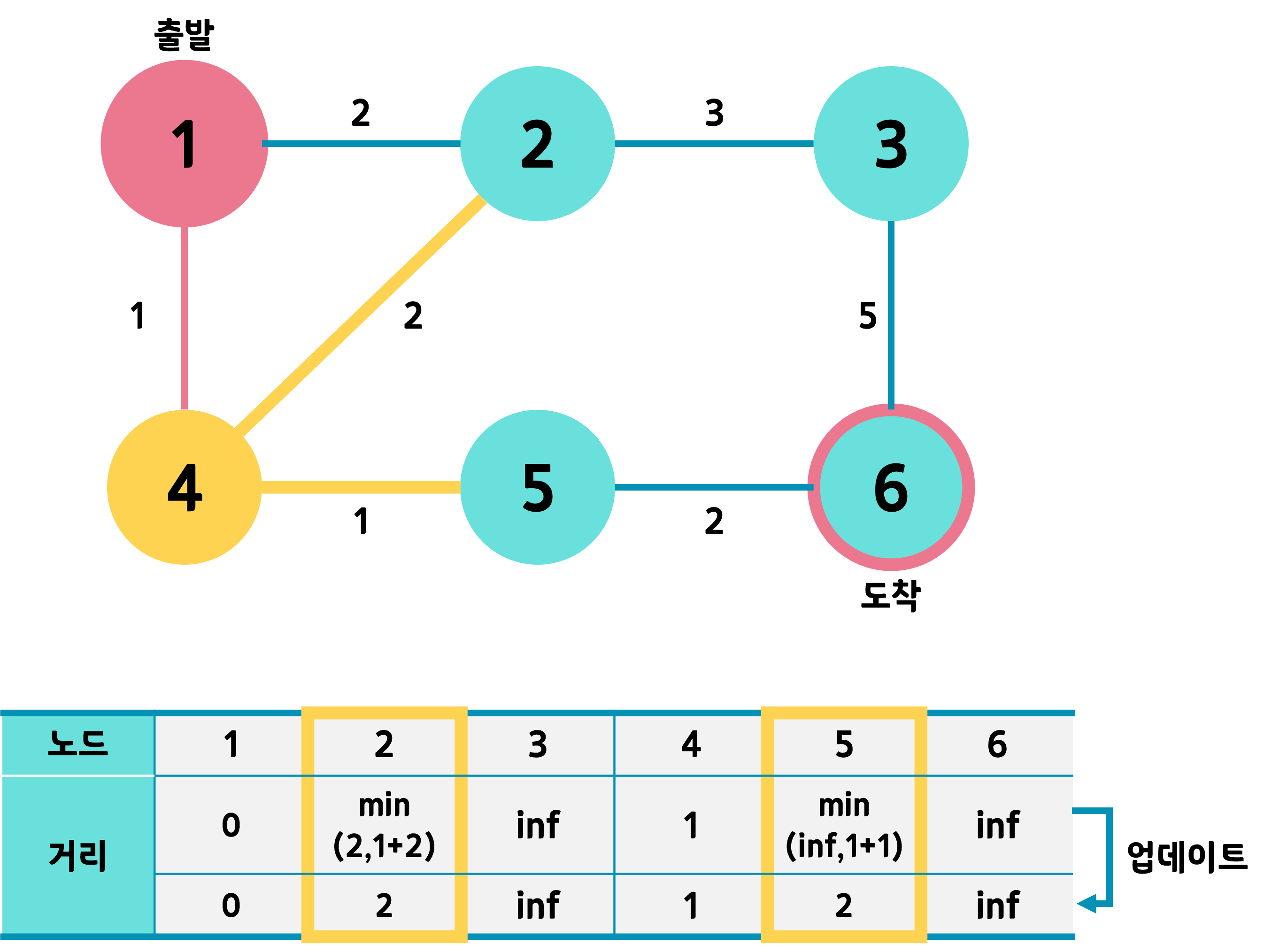
4번노드에서 갈 수 있는 방향은 2와 5이다.
2번노드로 가기위해서는 1번노드를 거쳐 3의 거리가 필요하고 5번 노드로 가기위해서는 1-4-5를 거쳐 2의 거리가 필요하다. 하지만 2번노드는 1-2로 바로 갈 수 있는 2의거리가 더 작으므로 2를 그대로 저장한다. 즉 2와 5로 가는 최단거리가 같으므로 더 작은 숫자를 택한다.

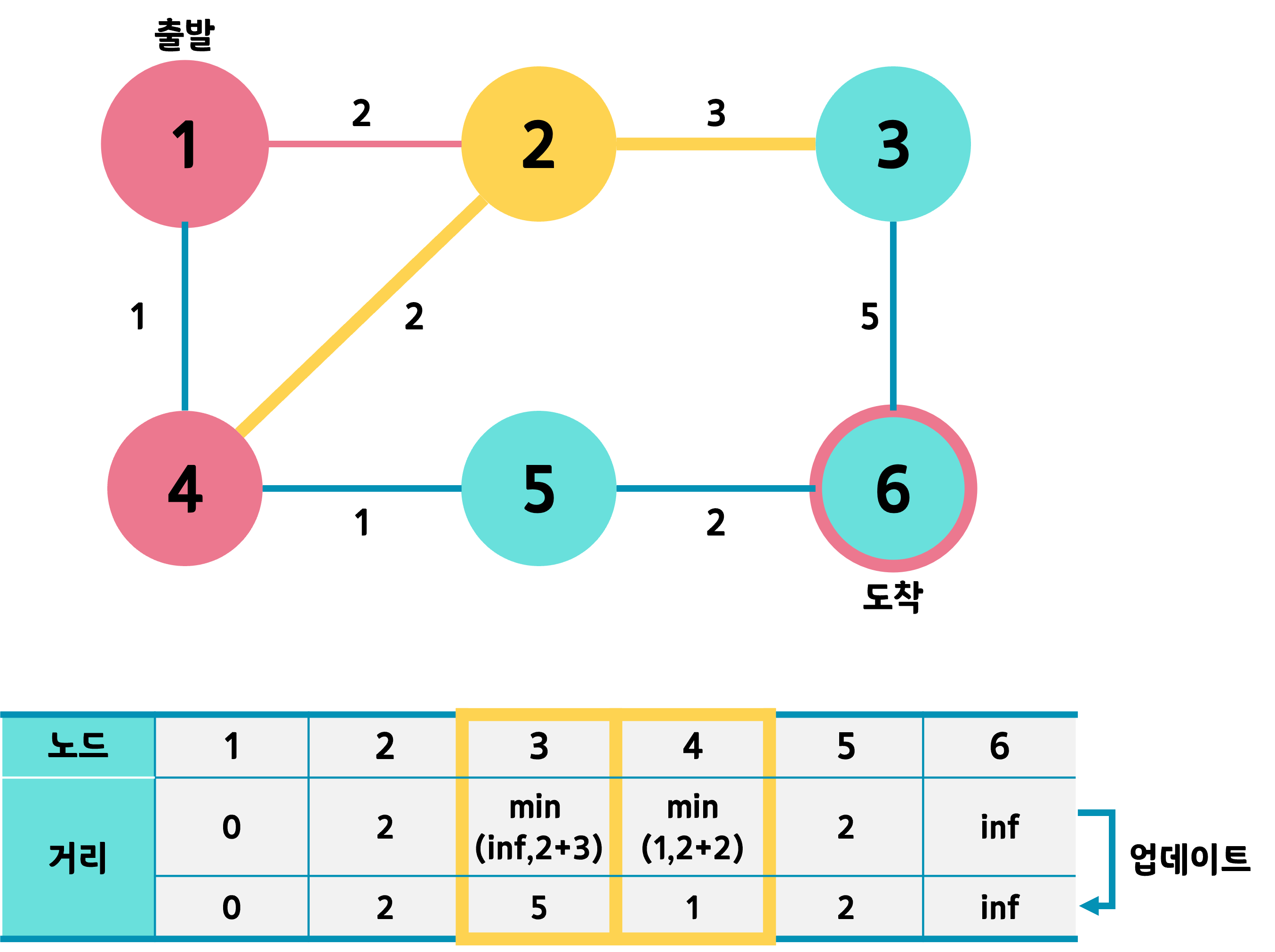
2번노드에서 3번노드와 4번노드를 갈 수 있다. 4번노드는 이미 방문했으니 3,5,6번노드를 갈 수 있는데 3까지 가기위해서는 1-4-2-3로 5의거리가 있고 5번노드는 거리가 2이기 때문에 5번노드로 이동한다

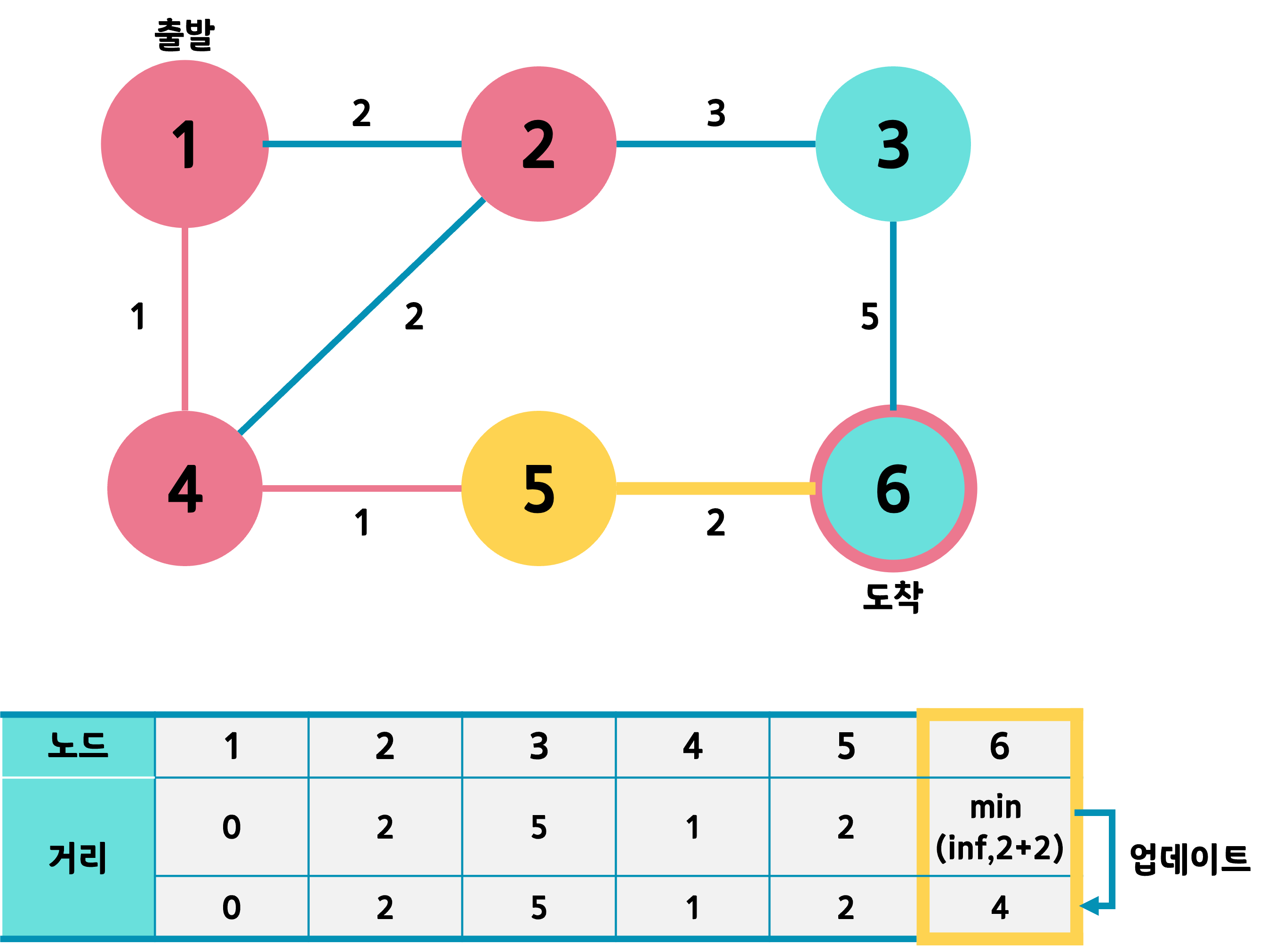
방문하지 않은 3,6번 노드 중에서 더 짧은 거리는 6번이고 6번이 도착노드이기때문에 6번으로 이동한다.

결국 6번노드까지 가는데 최단거리가 4인 1-4-5-6이다.

다익스트라 구현 방법

힙을 이용한 다익스트라 구현

import heapq


def dijkstra_pq(graph, start):
    N = len(graph)
    dist = [INF] * N

    q = []
    # 튜플일 경우 0번째 요소 기준으로 최소 힙 구조.
    # 첫 번째 방문 누적 비용은 0이다.
    heapq.heappush(q, (0, start))
    dist[start] = 0

    while q:
        # 누적 비용이 가장 작은 녀석을 꺼낸다.
        acc, cur = heapq.heappop(q)

        # 이미 답이 될 가망이 없다.
        if dist[cur] < acc:
            continue

        # 인접 노드를 차례대로 살펴보며 거리를 업데이트한다.
        for adj, d in graph[cur]:
            cost = acc + d
            if cost < dist[adj]:
                dist[adj] = cost
                heapq.heappush(q, (cost, adj))

    return dist