항해99 TIL 3주차 - 17

플로이드-워셜

플로이드-워셜이란?
모든 최단 경로를 구하는 알고리즘이다. 다익스트라 알고리즘도 최단경로를 구하는 알고리즘인데
둘의 차이점이 있다면 플로이드-워셜은 모든 노드간의 최단경로를 구할 수 있으며
다익스트라 알고리즘은 하나의 정점에서 다른 노드의 정점까지의 최단경로를 구할 수 있다.

플로이드-워셜 알고리즘 과정

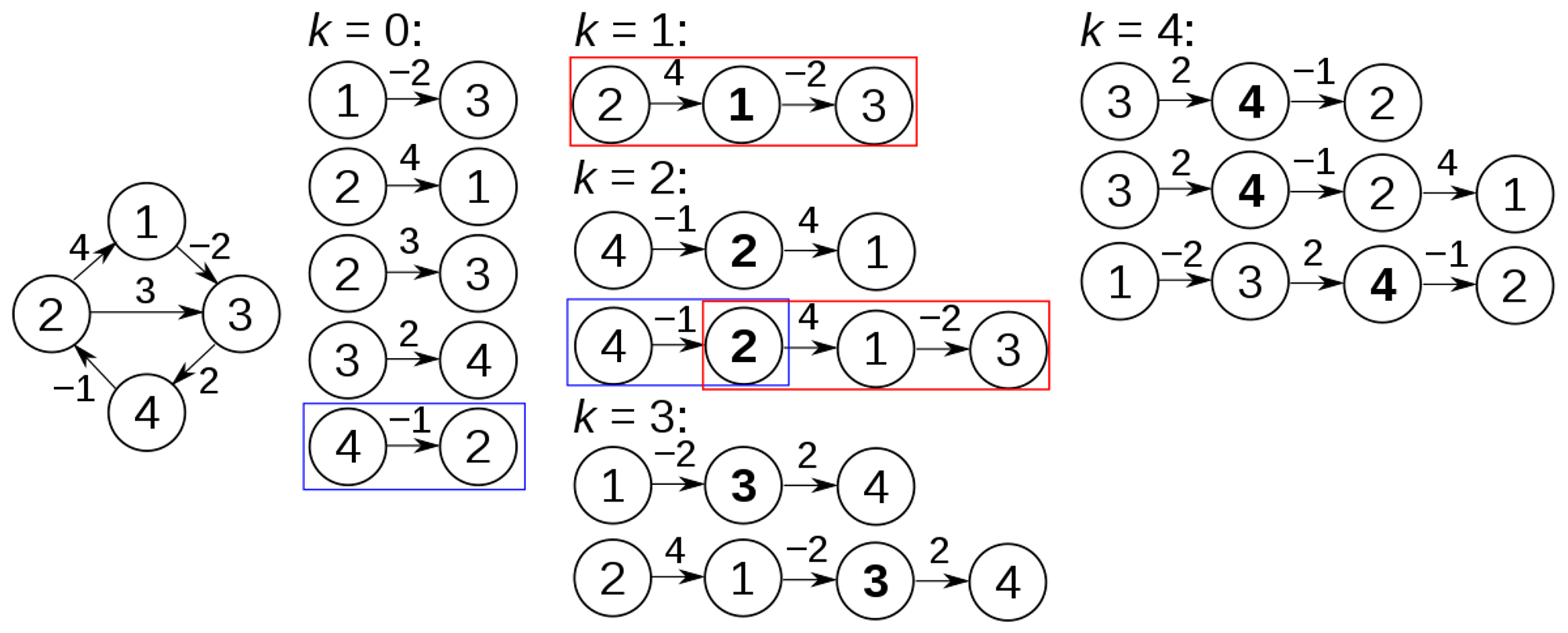
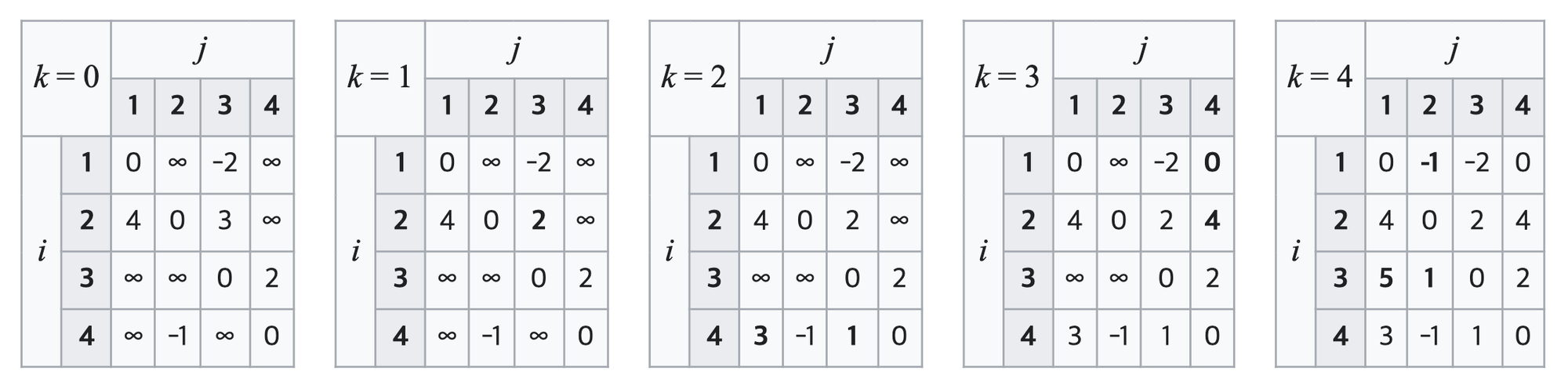
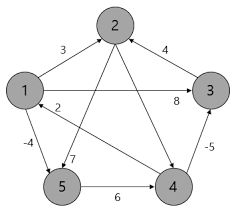
k=1 일때 1번노드를 중간노드로 설정할 경우 2 -1- 3 총 2의 길이로 갈 수 있다.

k=2 일때 2번노드를 중간노드로 설정할 경우 4-2-1이라면 3의 길이, 4-2-1-3라면 1의 길이로 갈 수 있다.

k=3 일때 3번노드를 중간노드로 설정할 경우 1-3-4이라면 0의 길이, 2-1-3-4라면 4의 길이로 갈 수 있다.

k=4 일때 4번노드를 중간노드로 설정할 경우 3,4,2라면 1의 길이, 3-4-2-1이라면 5의 길이, 1-3-4-2라면 -1의 길이로 갈 수 있다.

이 모든 과정을 거치면 최단경로의 길이를 구할 수 있다.

플로이드-워셜 구현

import sys
from collections import defaultdict
from pprint import pprint

from min_cost.floyd_warshall import floyd_warshall

def floyd_warshall(graph):
    N = len(graph)
    dist = [[INF] * (N + 1) for _ in range(N + 1)]

    for idx in range(1, N + 1):
        dist[idx][idx] = 0

    for start, adjs in graph.items():
        for adj, d in adjs:
            dist[start][adj] = d

    for k in range(1, N + 1):
        for a in range(1, N + 1):
            for b in range(1, N + 1):
                dist[a][b] = min(dist[a][b], dist[a][k] + dist[k][b])

    return dist
    
with open('testcase_fw.txt') as f:
    sys.stdin = f
    input = sys.stdin.readline
	INF = int(1e9)
    N = int(input())
    M = int(input())

    graph = defaultdict(list)
    for _ in range(M):
        a, b, c = map(int, input().split())
        graph[a].append((b, c))

    print(floyd_warshall(graph))