
- Sorting
-The values stored in an array have keys of a type for which the relational operators are defined. ( We also assume unique keys) : 크다 작다의 개념이 있다. ->순서가 생긴다.
-Sorting rearranges the elements into either ascending or descending order within the array. 재정렬- Ascending(오름차순,작->큰), Descending(내림차순, 큰->작)
Straight Selection Sort
: 마지막번째 Index부터 차레대로 I번째 인덱스까지 Scanning 하면서 최솟값을 찾는다. 찾은 최솟값을 i (0 <= i <= MAX_INDEX)번째 Index에 위치하도록 Swap한다.

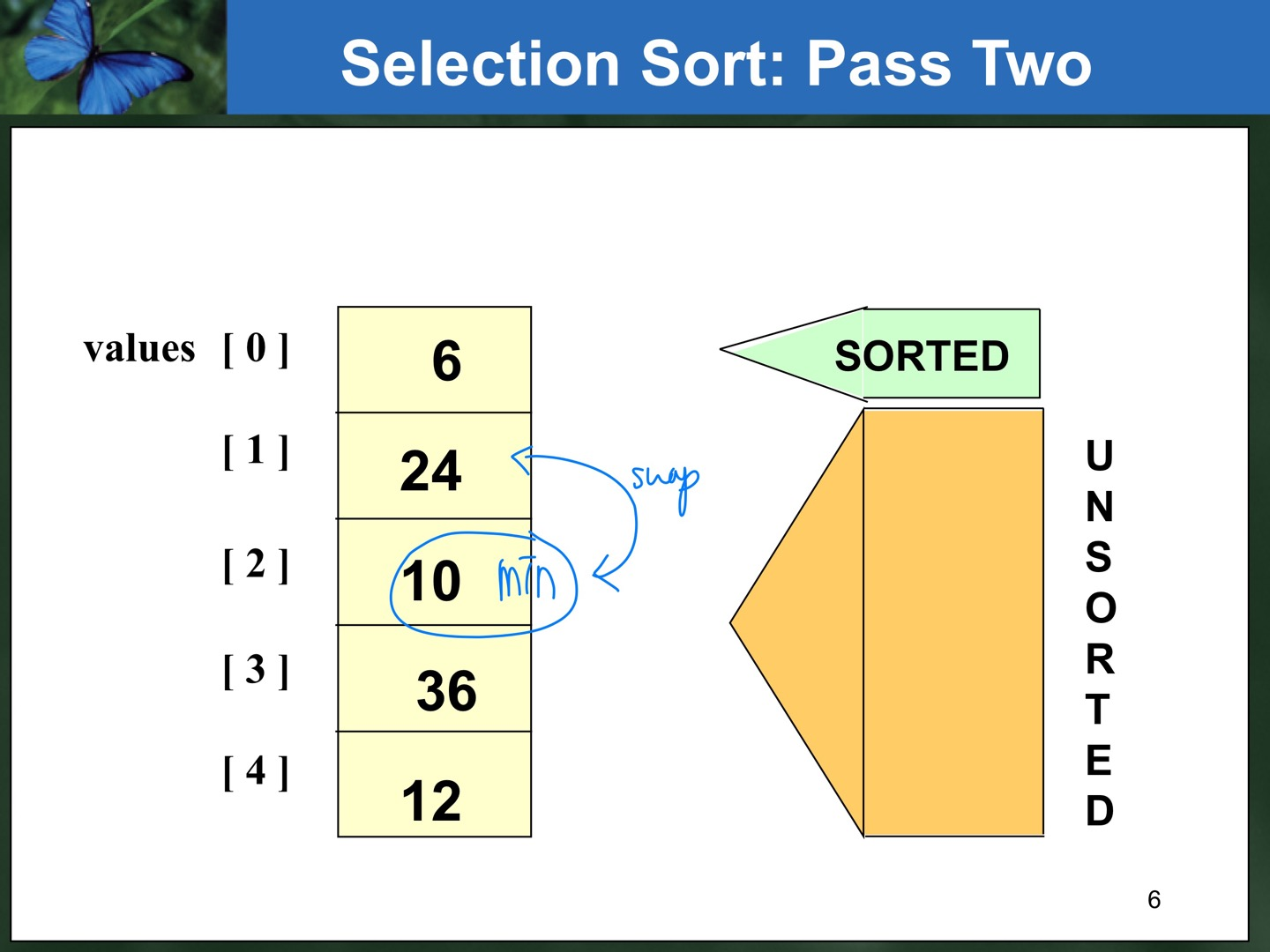
- 마지막 인덱스부터 찾고자 하는 위치까지 올라가며 살피며 그중에 최솟값을 찾으므로 N개의 값이 있다고 했을 때(인덱스는 0부터 N-1까지) N-1번 비교, N-2번 비교, ..., 1번 비교 하게 된다.


template<class ItemType>
int MinIndex(ItemType values[], int start, int end)
{
int indexOfMin=start;
// scanning ; O(N)
for(int index=start+1; index<=end; index++)
{
if (values[index] < values[indexOfMin] )
indexOfMin=index;
}
return indexOfMin;
}template<class ItemType>
void SelectionSort(ItemType values[], int numValues)
{
int endIndex=numValues-1;
// Minindex() 에서 for 중첩 : O(N^2)
for(int current=0; current<endIndex; current++)
// current:고정시킬 위치. endIndex는 알아서 자기자리에 와있으므로 등호포함X
{
Swap(values[current], values[Minindex(values, current, endIndex)]);
}
}Bubble Sort
: 맨 아래서부터 위로 올라가면서 두 pair씩 비교하고, 비교할 때마다 작은 값이 위로 가도록 Swap해준다. 전체 Scan 1회마다 1개씩 정렬된다는 보장이 있다.

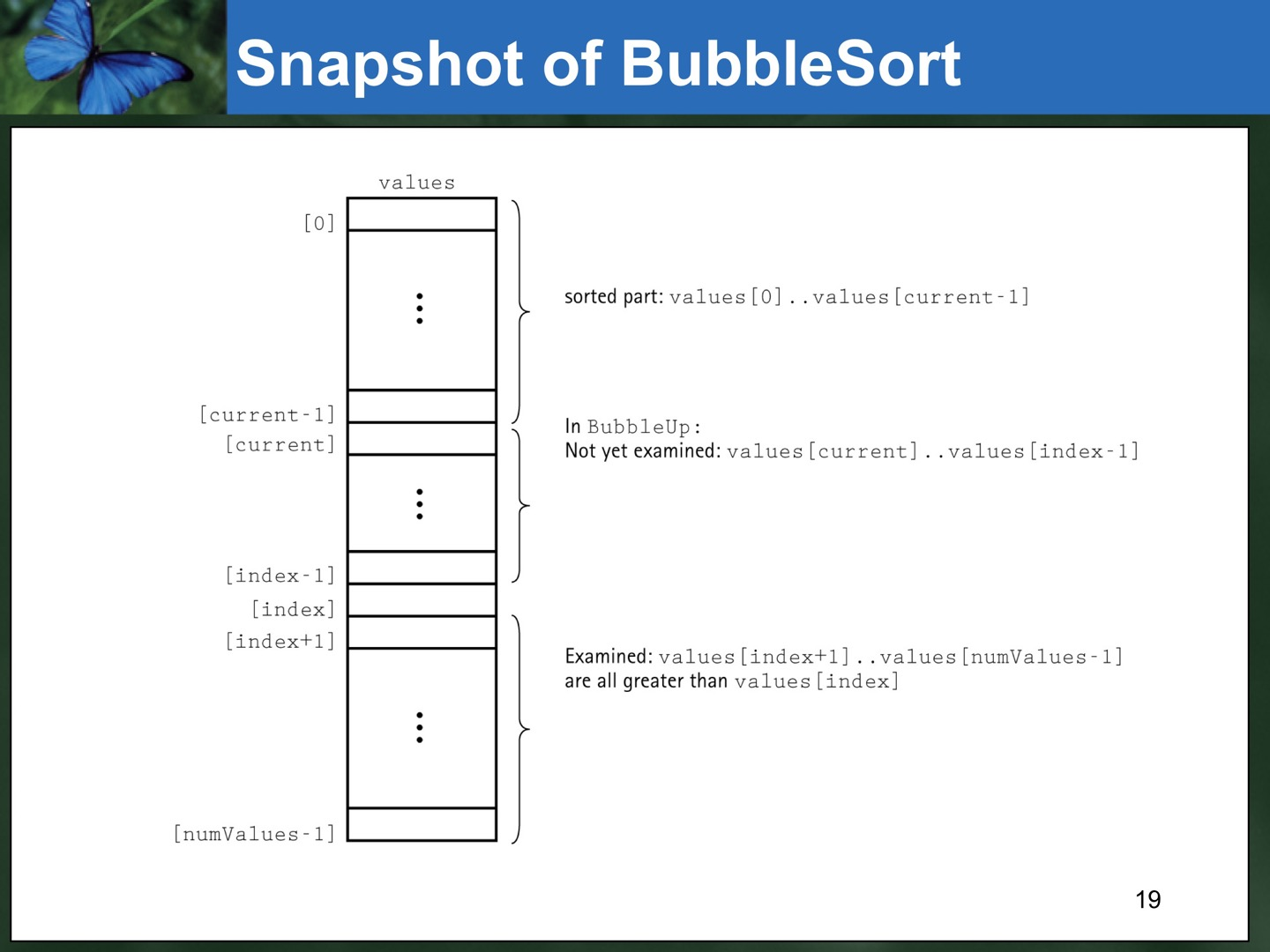
- 마찬가지로 한 바퀴를 돌 때마다 하나의 위치씩 제자리를 찾아가 고정이 된다. 따라서 비교횟수는 총 N개의 원소가 있을 때(0번 Index부터 N-1번 Index까지 있을 때) N-1번, N-2번, ..., 1번이 되므로 마찬가지로 O(N^2)이 된다.

template<class ItemType>
void BubbleSort(ItemType values[], int numValues)
{
int current=0;
// BubbleUp에서도 for문을 돌기때문에 While까지 해서 반복문 중첩. O(N^2)이 된다.
while(current<numValues-1) // numValues-1 : endIndex. 처음부터 마지막 전까지.
// 마지막 인덱스는 정렬하지 않아도 마지막 전까지 정렬하면 알아서 자기 자리 찾으므로 등호 포함하지 않는다.
{
// current : 하나씩 증가한다. , numValues-1 : endIndex는 고정된다.
BubbleUp(values, current, numValues-1);
current++;
}
}template<class ItemType>
void BubbleUp(ItemType values[], int startIndex, int endIndex)
{
// endIndex부터 위치 찾을 인덱스(startIndex) 전까지 반복문 실행한다.
for(int index=endIndex; index>startIndex; index--)
{
if(values[index] < values[index-1]) // 자신의 바로 앞과 비교한다.
Swap(values[index], values[index-1]);
}
}Insertion Sort

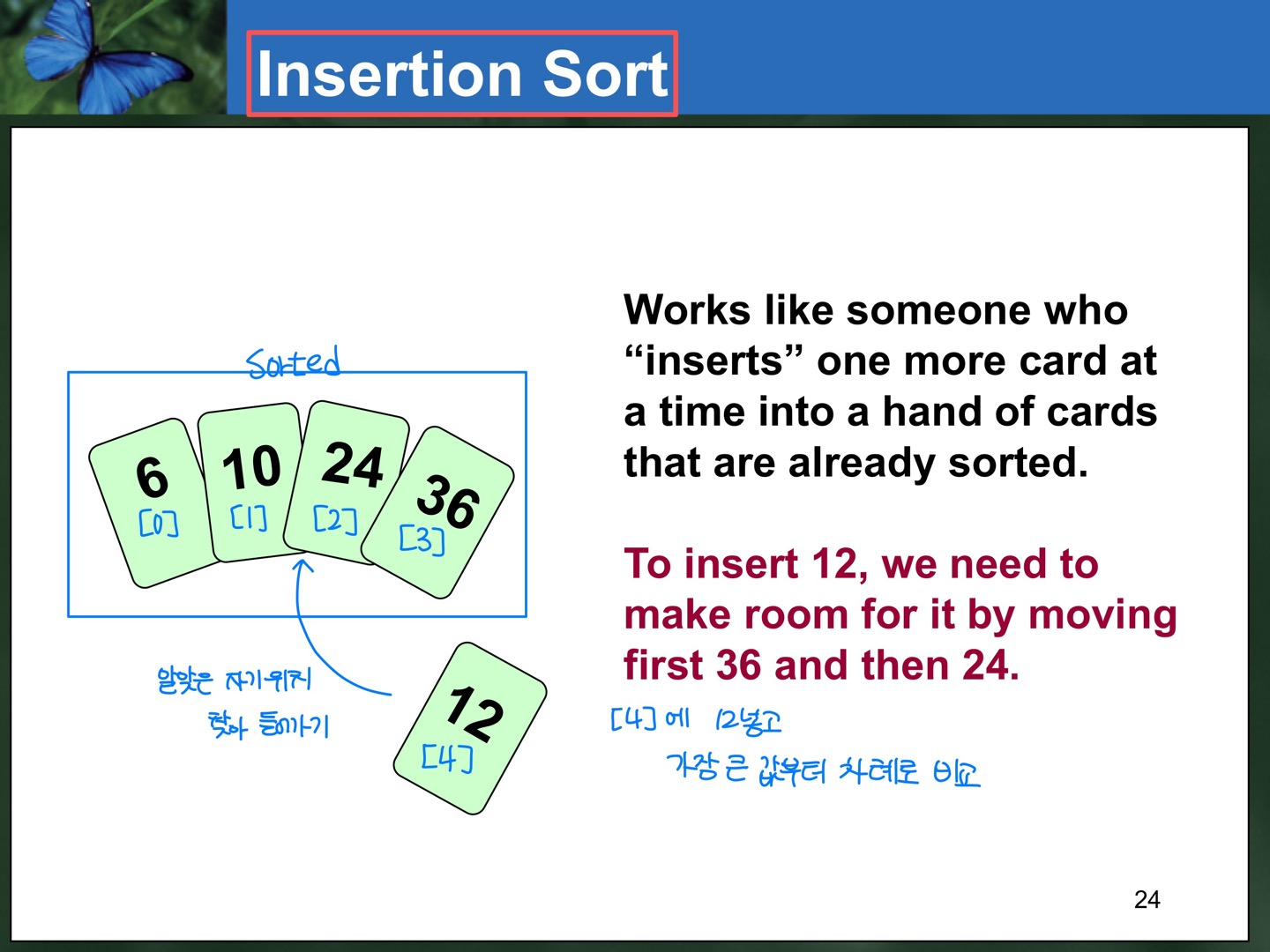
template<class ItemType>
void InsertItem(ItemType values[], int start, int end)
{
bool finished=false;
int current=end; // initial state : 고정할 위치 에서 시작
bool moreToSearch=(current!=start); // 고정할 위치에서 처음까지 다 돌면 끝
// while : O(N)
while(moreToSearch && !finished)
{
if(values[current]<values[current-1]) // 자신의 앞 칸과 비교
{
Swap(values[current], values[current-1]);
current--; // 앞으로 간다
moreToSearch=(current!=start);
}
else
finished=true; // 내 자리 찾으면 끝나고 나온다
}template<class ItemType>
void InsertionSort(Itemtype values[], int numValues)
{
// for문 : InsertItem에서도 while문 돌기 때문에 반복문 중첩으로 O(N^2)이 된다.
for(int count=0; count<numValues; count++) // count는 고정할 위치
InsertItem(values, 0, count);
}Sorting Time Complexity
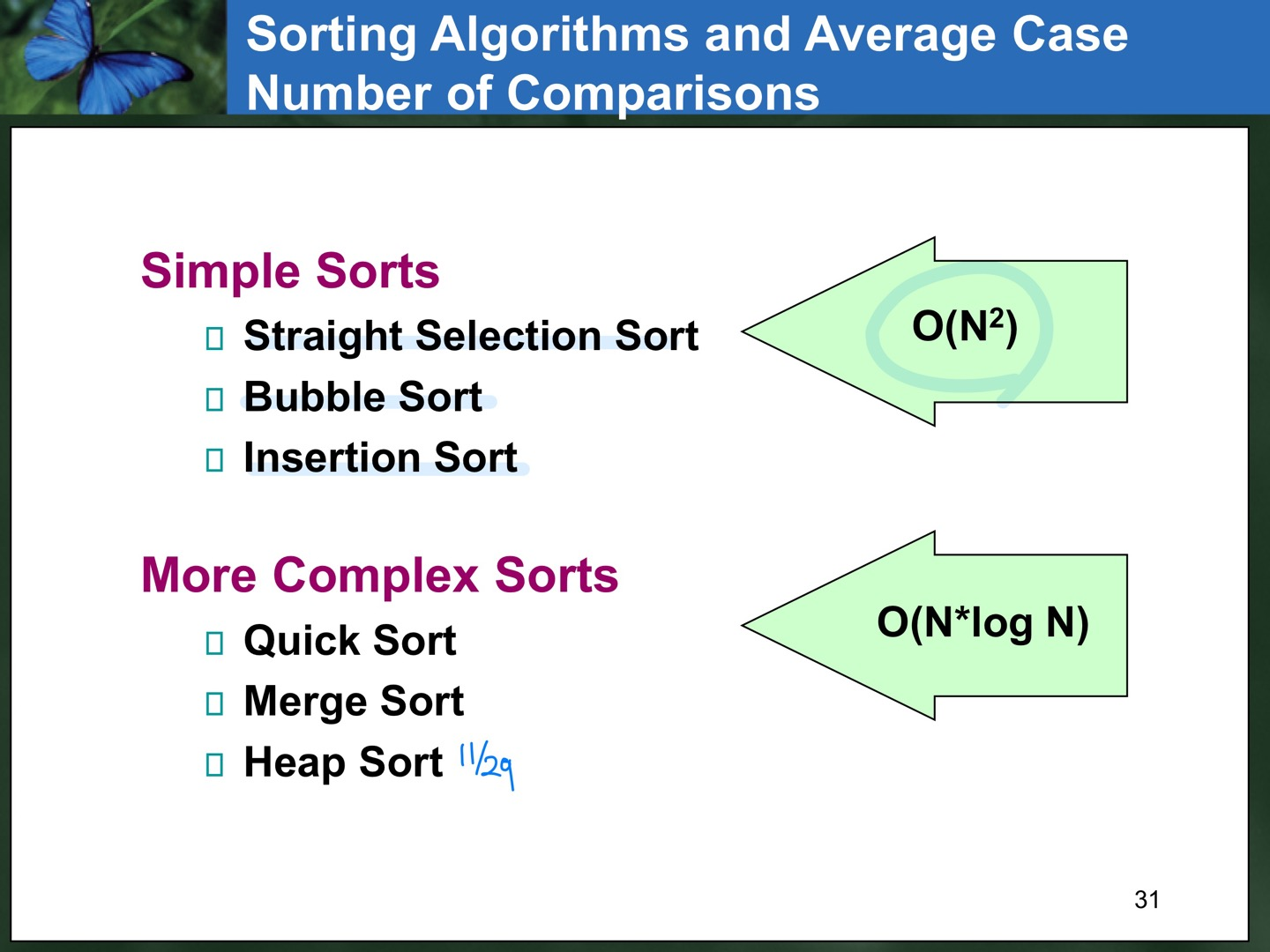
Heap Sort
- Recall) Heap
📌 Heap은 Complete Binary Tree이며 현재 우리는 Max Heap형태로 구현했다.(가장 큰 값이 가장 위에 위치). 가장 작은 값이 가장 위에 위치하는 Min Heap 형태도 가능하다.
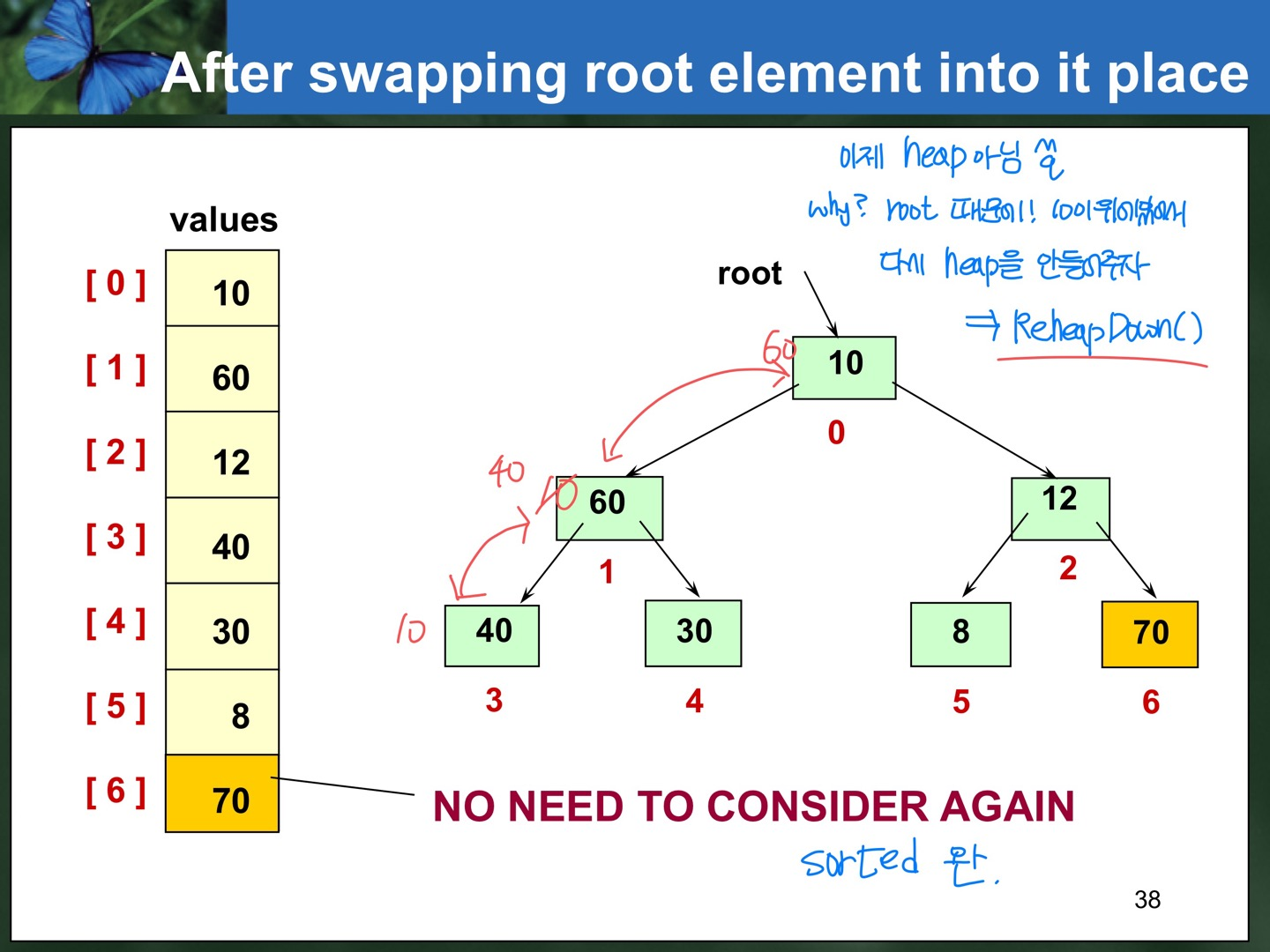
📌 Max Heap에서 우리가 알고 있는 값은 root가 가리키는(0번 인덱스) 가장 큰 값 뿐이다. 이 값을 제일 끝 값과 Swap시키고 ReHeapDown 시키는 과정을 반복하면 Array가 Ascending sorted가 된다.
- Time Complexity 계산
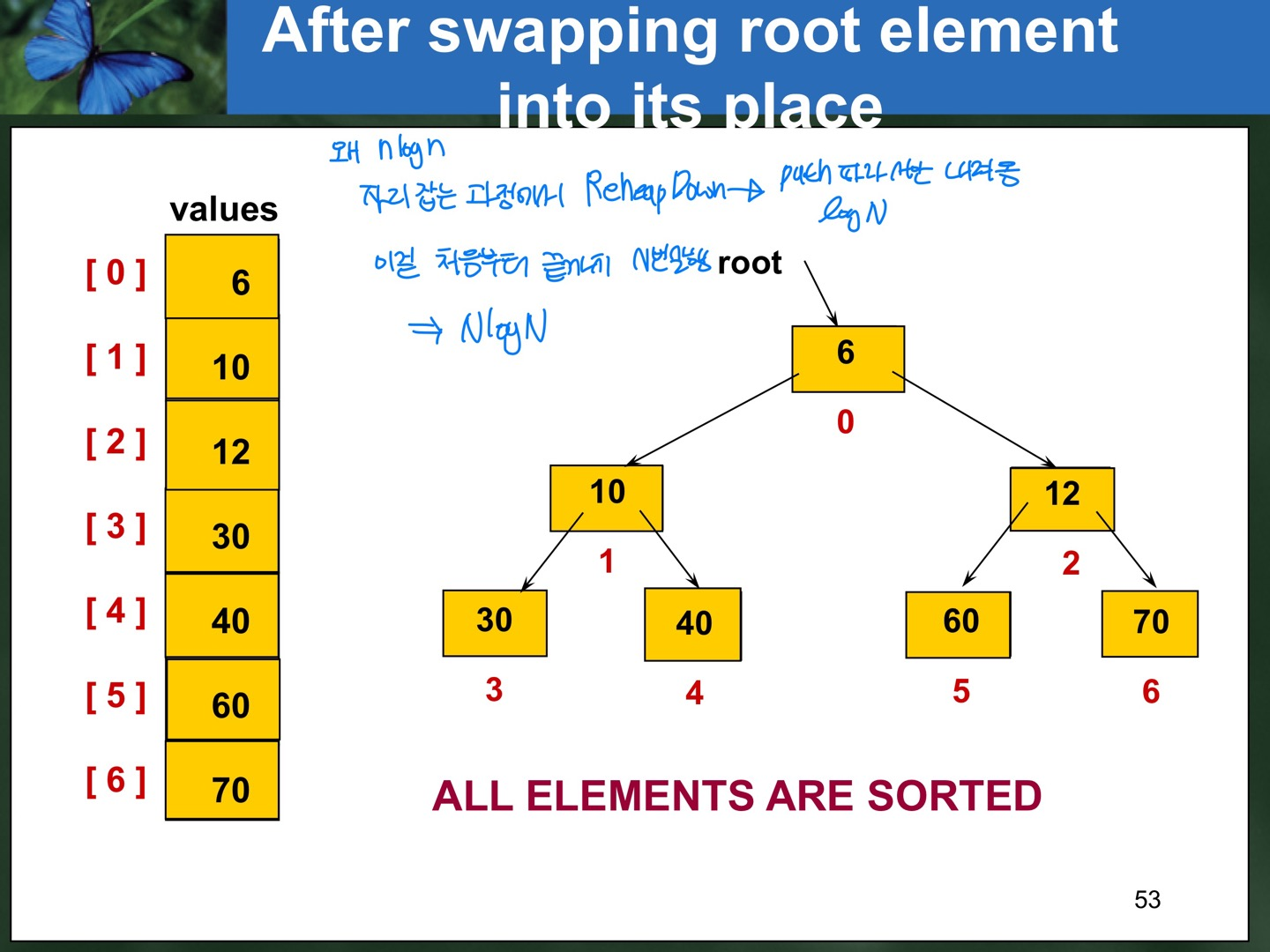
: 가장 끝 인덱스부터 하나씩 자기 자리가 고정되고 이 자리 잡는 과정마다 ReheapDown이 한 번씩 된다. ReheapDown은 Path를 따라서만 내려오므로 시간 복잡도가 logN이고, 이 ReheapDown을 처음부터 끝까지 N번 실행하므로 Heap Sort의 시간 복잡도는 NlogN이 된다.
=> heap을 만들 때 (N/2)O(logN)이다. loop를 반만 돌면서 HeapDown하기 때문이다.
=> heap을 정렬할 때 (N-1)O(logN)이다. 처음부터 끝 전까지 돌면서 HeapDown하기 때문이다.
=> 이 둘을 합하면 O(NlogN)이 된다.
template<class ItemType>
void HeapSort(ItemType values[], int numValues)
{
int index;
// Array를 heap으로 만들어준다. 이때도 nlogN time complexity가 발생한다.
// Non terminal node에 대해서 ReheapDown을 해서 array를 heap으로 만드는 방법
// Terminal node에 대해서 ReheapUp을 해서 array를 heap으로 만드는 방법도 가능하다.
// 똑같이 Time complexity는 nlogN이 된다.
for(index=numValues/2-1; index>=0; index--)
// leaf노드 시작 지점 전까지, root까지, 아래서 위로
ReheapDown(values, index, numValues-1);
// array를 정렬한다. 이때도 nlogN time complexirt가 발생한다.
for(index=numValues-1; index>=1; index++)
//가장 뒤부터 자리잡는다, 0은 알아서 정렬되므로 1까지만, 젤 뒤에서 앞으로 한 칸씩
{
Swap(values[0], values[index]);
// root(가장큰값), 고정시킬위치
ReheapDwon(values,0,index-1);
// 0부터 index-1까지 내려가게 하는 Reheapdwon
}
}
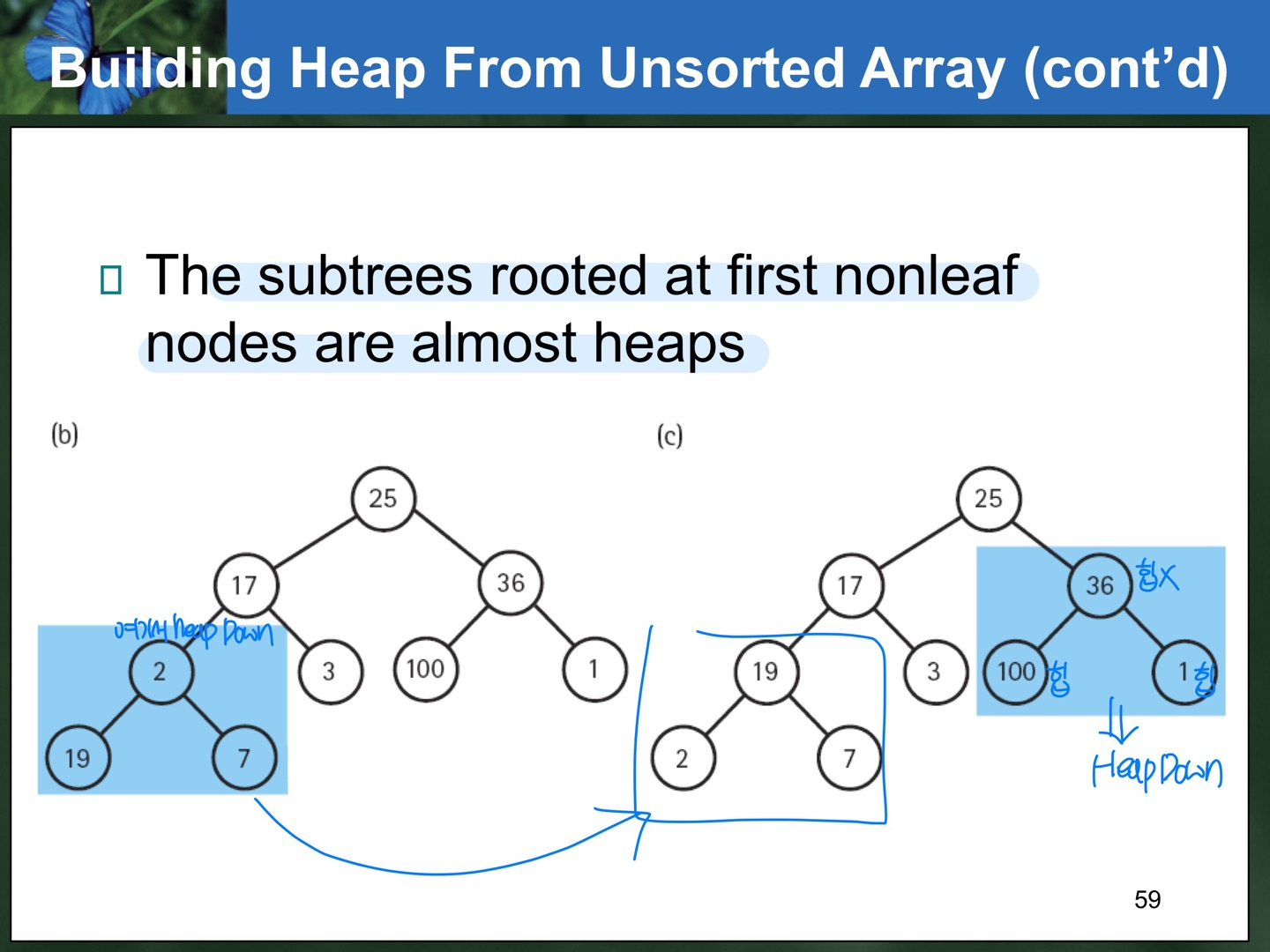
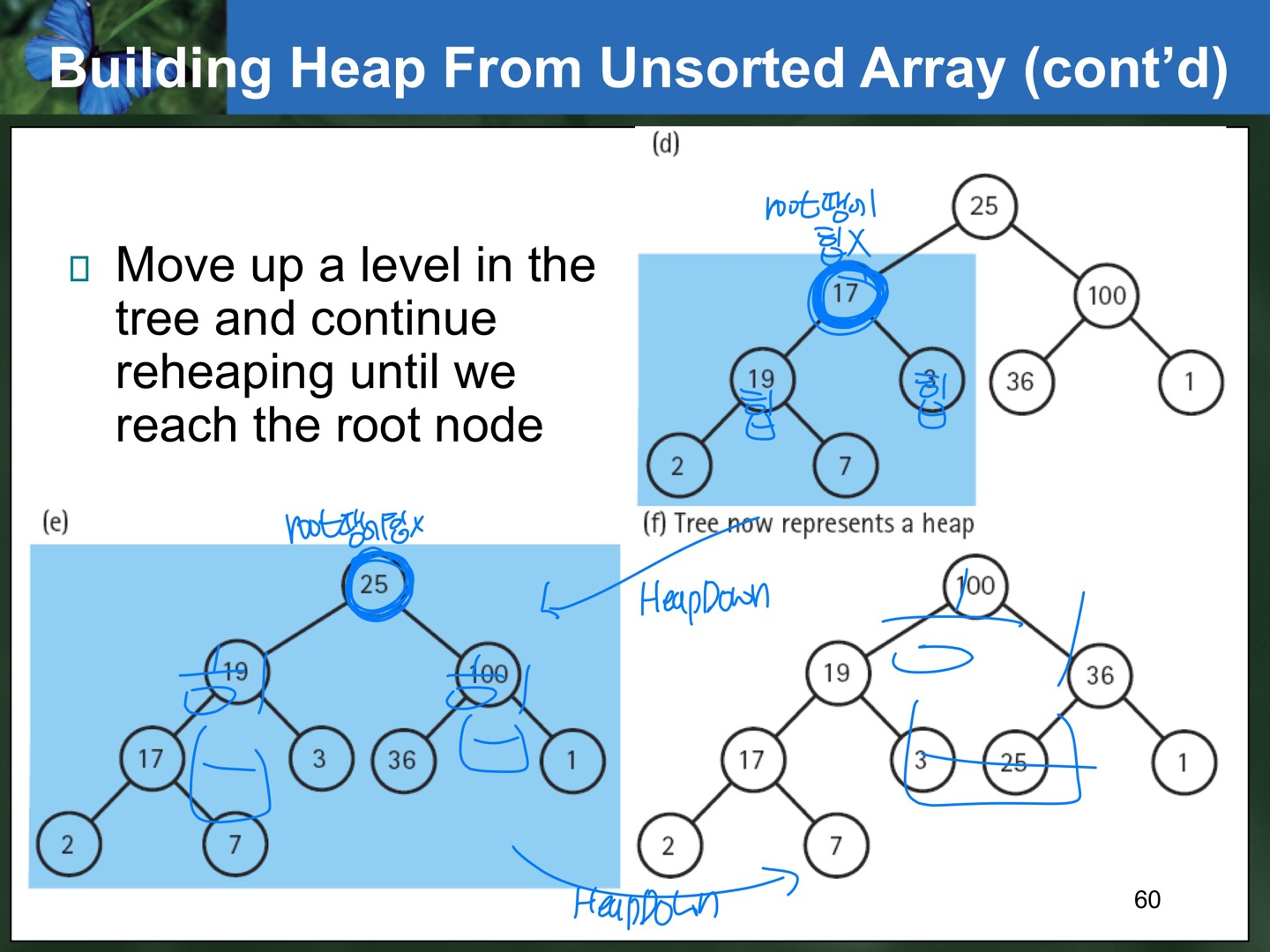
- Array를 ReHeapDown 시켜서 Heap을 만드는 과정
// Recall ) ReHeapDown
template<class ItemType>
void ReHeapDown(ItemType values[], int root, int bottom)
{
int maxChild;
int rightChild;
int leftChild;
leftChild=root*2+1;
rightChild=root*2+2;
if(leftChild<=bottom)
{
if(leftChild == bottom )
maxChild=leftChild;
else
{
if(values[leftChild] <= values[rightChild])
maxChild=rightChild;
else
maxChild=leftChild;
}
if(values[root] < values[maxChild])
{
Swap (values[root], values[maxChild]);
ReHeapDown(maxChild, bottom);
}
}- 가운데부터(Leaf nodes는 이미 Heap이기 때문이다) 앞으로 가면서 HeapDown을 부르면 전체가 Heap이 된다.
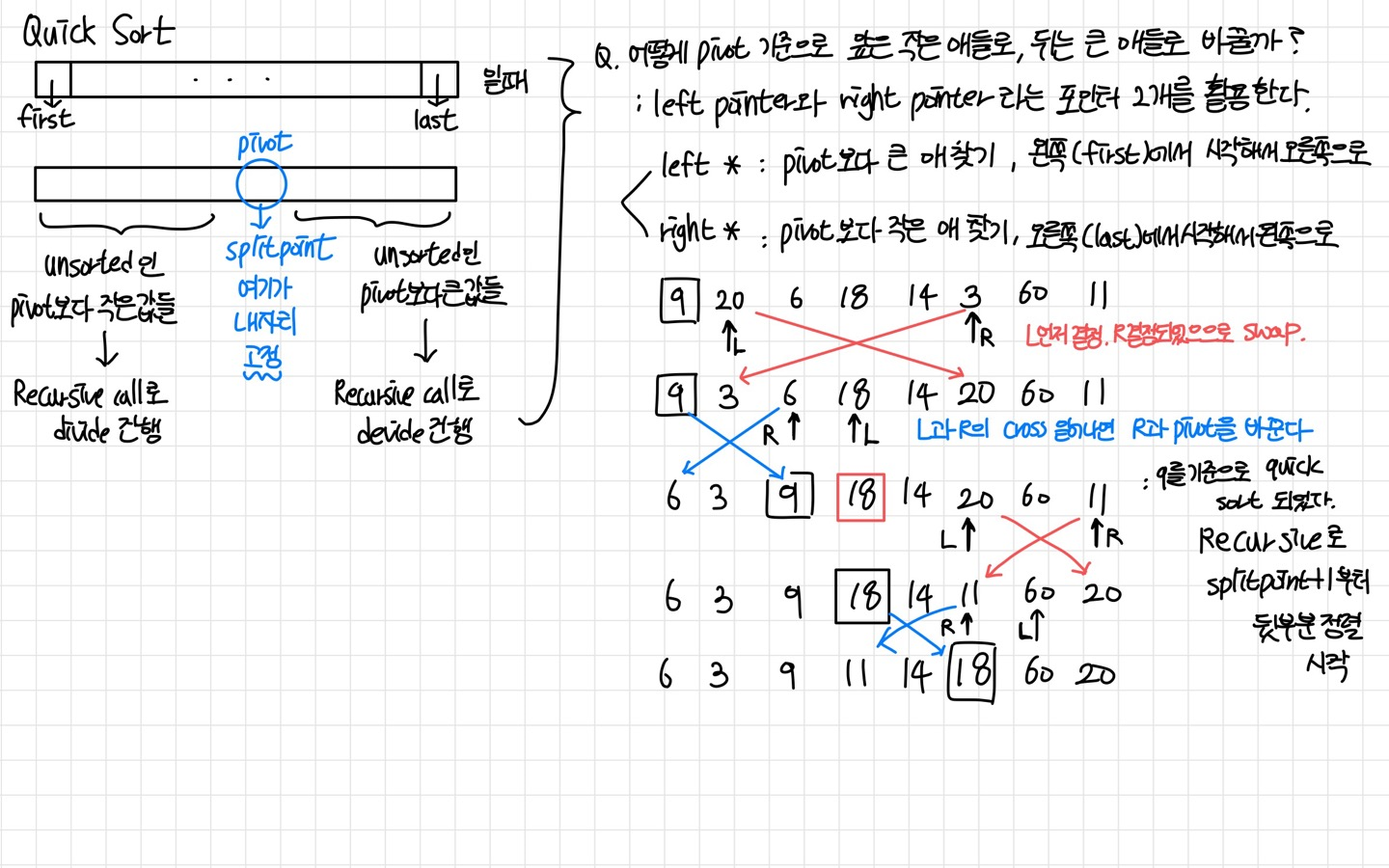
Quick Sort
: Quick Sort는 우선 SplitPoint를 기준으로 SplitPoint의 인덱스 값보다 앞에는 작은 값들, 뒤에는 큰 값이 오도록 하는 과정을 반복하며 정렬하는 것이다. Divide and Conquer 원칙을 따른다.
template<class ItemType>
void QuickSort(ItemType values[], int first, int last)
// 어디서부터 어디까지
{
if(first<last) // general case
{
int splitPoint;
// 어떻게 자리를 찾는지 과정이 중요하다.
Split(values, first, last, splitPoint);
// values[splitPoint]보다 작은 값들 모아두게 divide하고 Recursive call
QuickSort(values, first, splitPoint-1);
// vluaes[splitPoint]보다 큰 값들 모아두게 divide하고 Recursive call
QuickSort(values, splitPoint+1, last);
}
// base case : first >= last인 경우
}
- Time Complexity of Quick Sort
: Split을 하면 절반씩 도는 범위가 줄어들기 때문에 일반적으로는 NlogN이다.
첫 번째는 N, 두 번째는 2(N/2), 다음은 4(N/4) ... 식으로 쪼개진다. 만약 역순으로 정렬되어있는 array를 Quick Sort를 통해 정렬하려고 하면 전부 다 봐야 하므로 Selection Sort와 동일한 과정을 거치게 되고 Worst Case는 O(n^2)가 된다.
Merge Sort
template<class ItemType>
void MergeSort(ItemType values[], int fisrt, int last)
{
if(first<last)
{
int middle=(first+last)/2; // 가운데 인덱스를 찾는다.
MergeSort(values, first, middle); //반으로 쪼갠 앞부분
MergeSort(values, middle+1, last); //반으로 쪼갠 뒷부분
//쪼개놓고 다시 합칠 때 정렬이 되도록 합친다.
Merge(values, first, middle, middle+1, last);