[자료구조] Chapter 9. Priority Queues, Heaps, and Graphs (2)

nothingisme·2022년 12월 11일

[자료구조]

목록 보기

5/6

Graph Definition

A data structure that consists of a set of nodes(vertices) and a set of edges that relate the nodes to each other
The set of edges describes relationships among the vertices - 노드끼리의 관계를 줄로 이어주는 것

A Graph G is defined as follows : G=(V,E)

V(G) : a fininte, nonempty set of vertices - vertex 집합

E(G) : a set of edges(pairs of vertices) - edge 집합

📘 Directed vs Undirected Graphs 📘

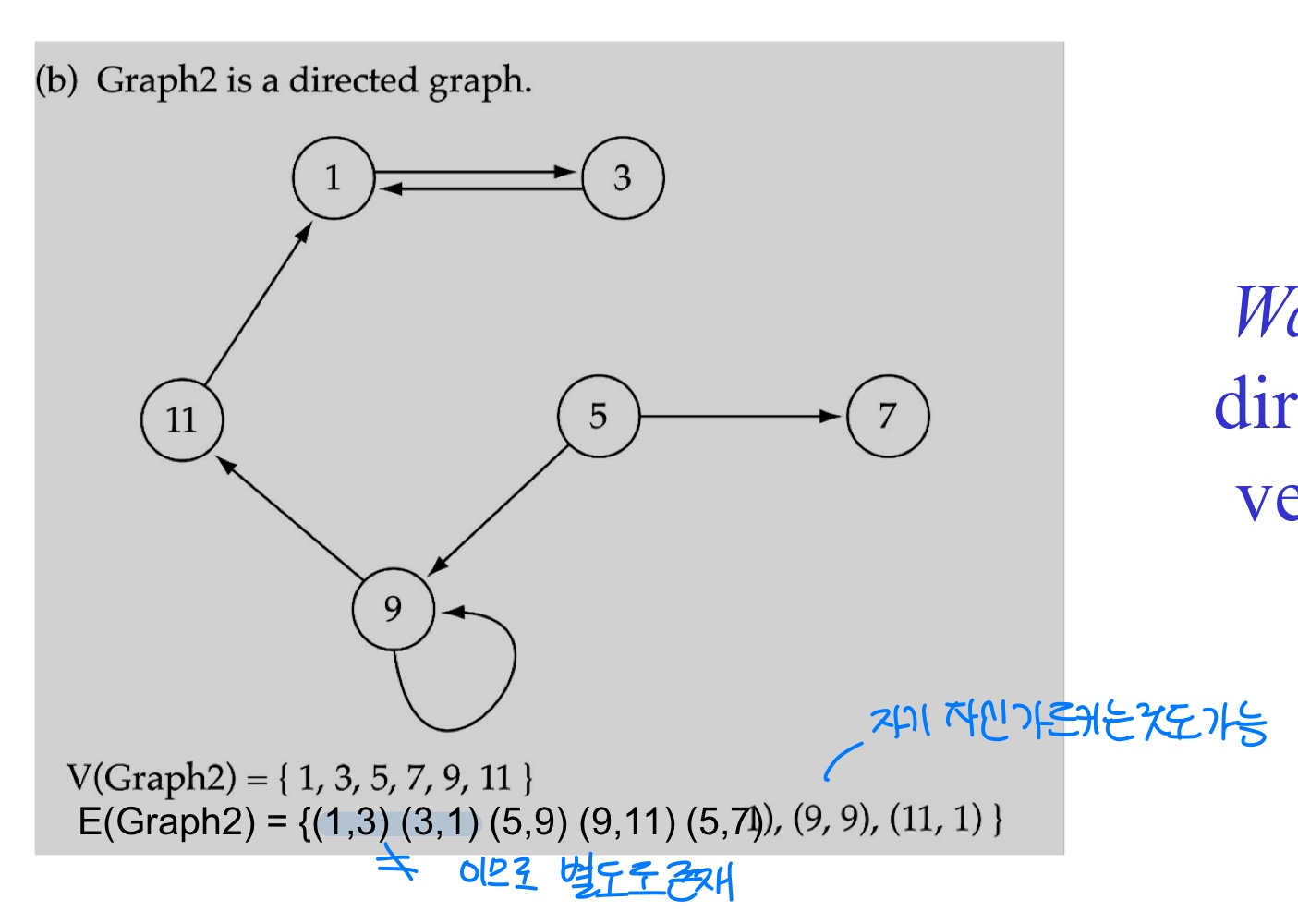
Directed Graphs : 모든 edged가 방향성(화살표)이 있는 graph

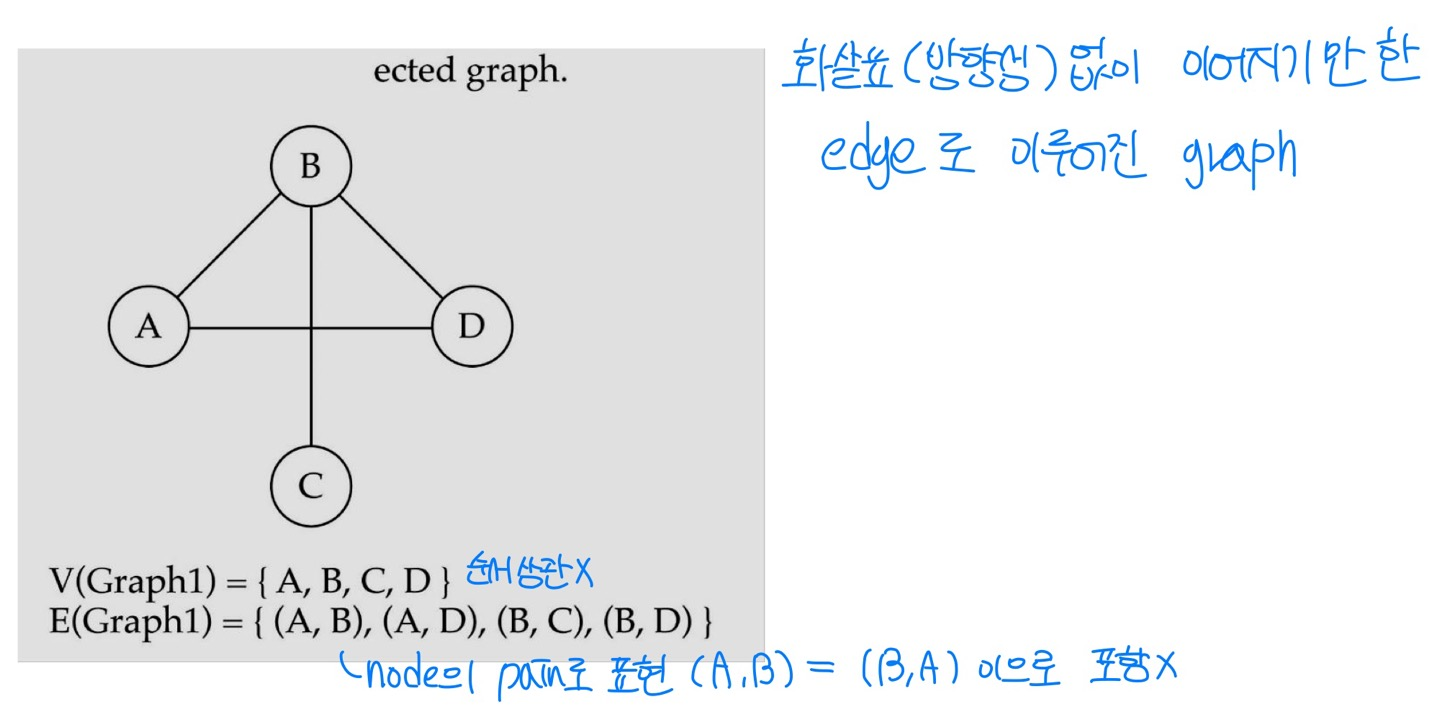
Undirected Graphs : 방향성(화살표) 없이 이어지기만 한 edge로 이루어진 graph

Tree는 parent에서 child로 방향이 있는 edge로 이루어진 graph이다. path가 unique하고 자기 자신을 가르키지 못한다.

📘 Graph Terminology 📘

Adjacent nodes(이웃한 노드) : two nodes are adjacent if they are connected by an edge
( node : 5 ) -> ( node : 7 ) 이면 5 to 7 또는 7 from 5 라고 말할 수 있다.

Path : a sequence of vertices that connect two nodes in a graph
두 vertex 사이를 connecting 하는 sequence(= edge의 sequence = vertex의 sequence)

Complete graph : a graph in which every vertex is directly connected to every other vertex
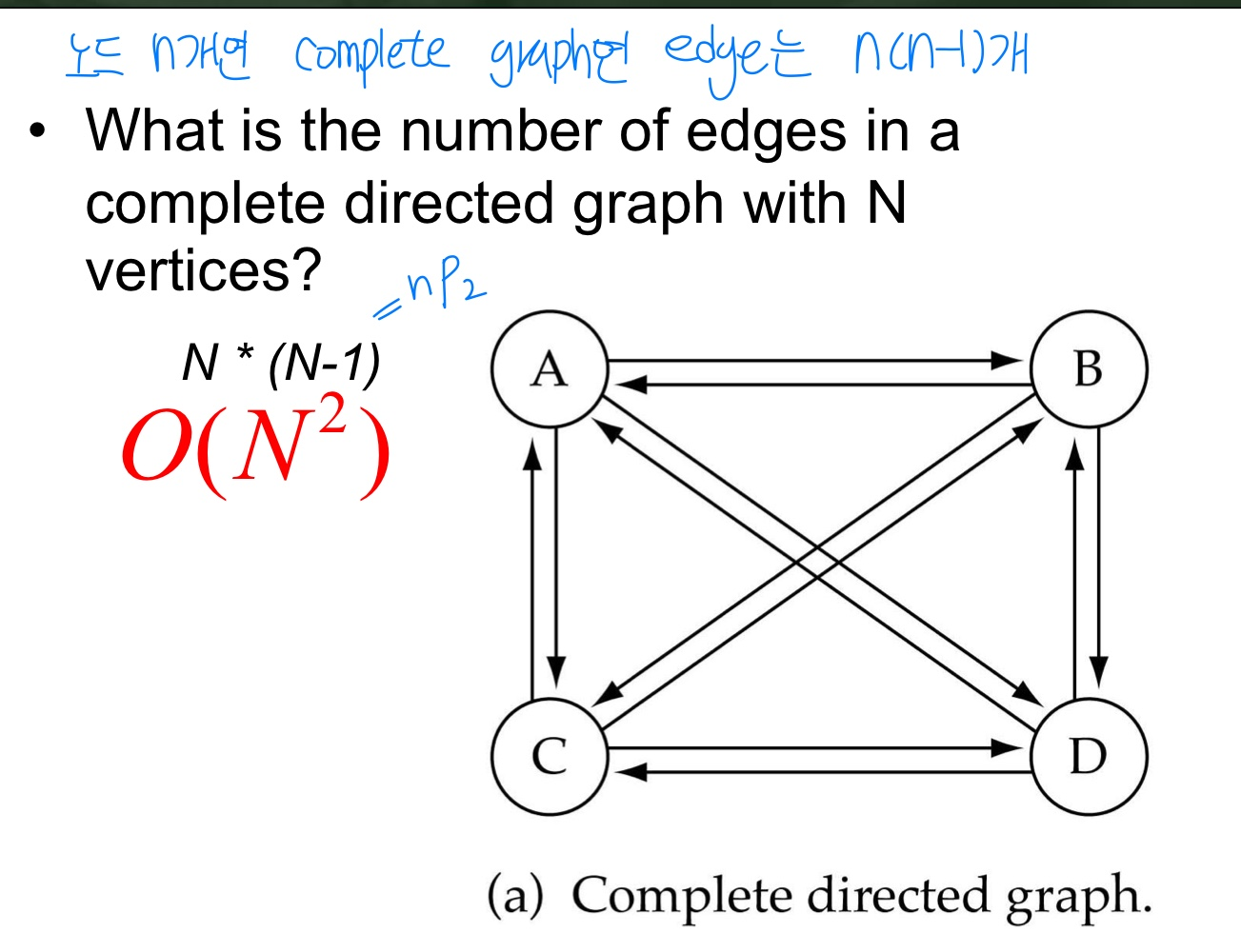
= 모든 vertex 사이에 edge가 있는 graph
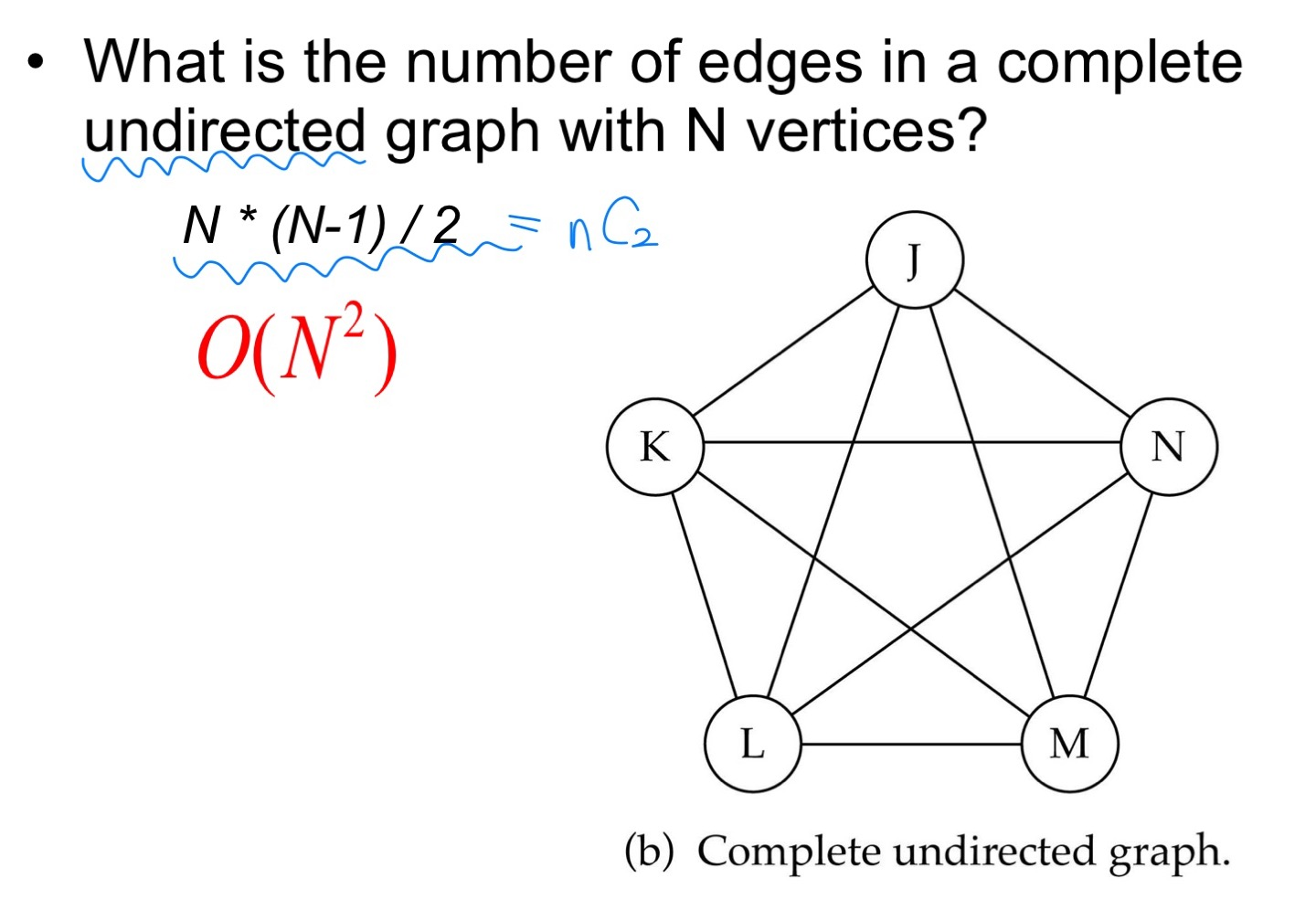
Q. N 개의 노드를 가진 Complete directed graph의 edge 개수 -> 순열 Permutaion

Q. N 개의 노드를 가진 Complete undirected graph의 edge 개수 -> 조합 Combination

Weighted graph : a graph in which each edge carries a value
= 상대적 중요도를 표시한 그래프. direct/undirect 모두 가능하다

Graph Implementaion

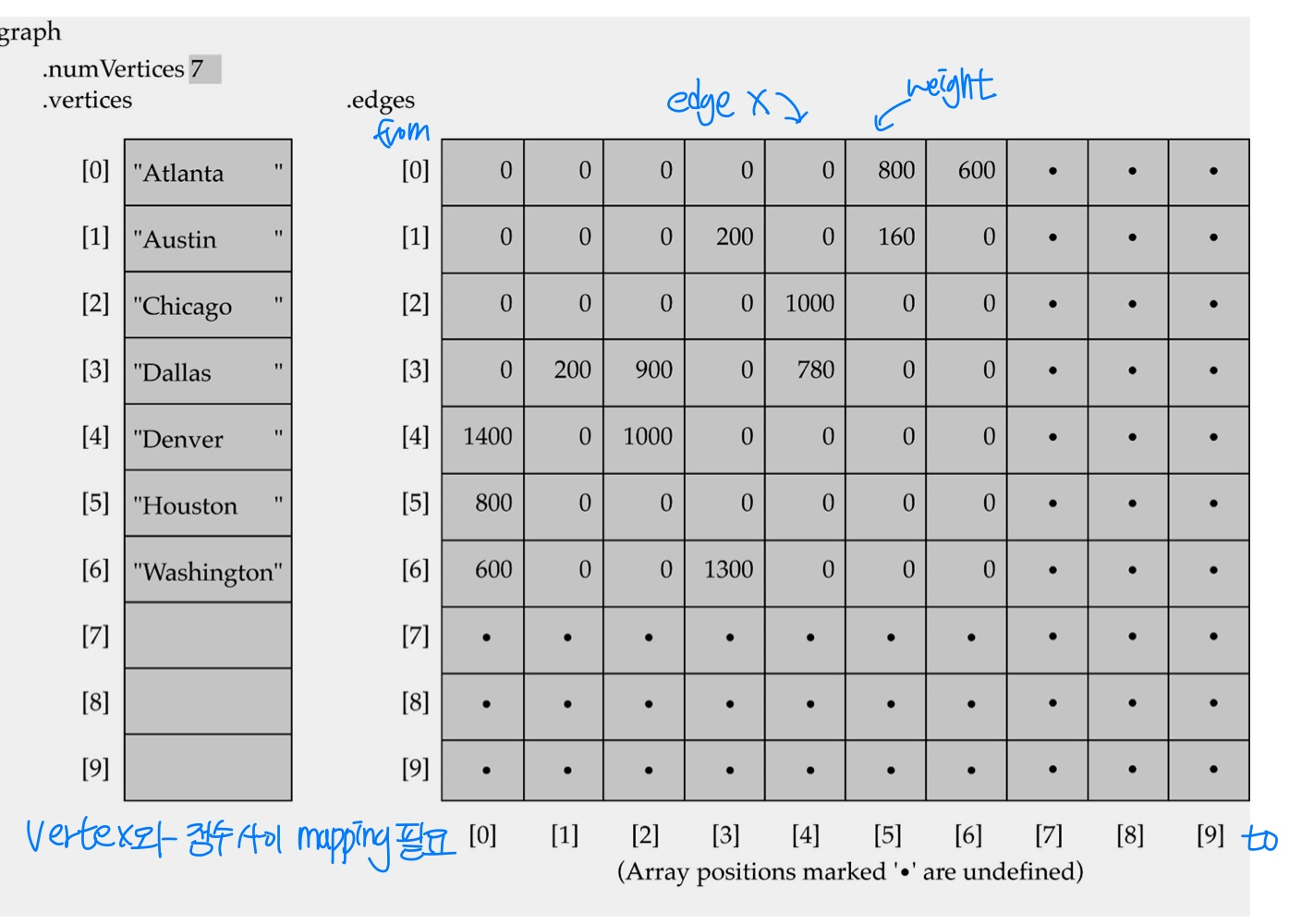
1. Adjacency Matrix : Array-based implementation

1D array is used to represent the vertices
2D array (adjacency matrix) is used to represent the edges
장점 : tree와 달리 (tree는 최대 2개) 한 node에서 point할 node의 개수가 제약이 없으므로 linked-list보다 array가 더 쉽다.
단점 1: 그러나 노드 개수가 많은데 edge 수는 적은 (sparsed graph) 경우에는 메모리 비효율적이다. array-based로는 graph가 Dense일 때만 효율적이다.
단점 2: 새 노드가 생겼을 때 정렬이 불가능하기 때문에 노드를 찾을 때 반드시 Linear Search를 해야 한다는 문제도 있다.

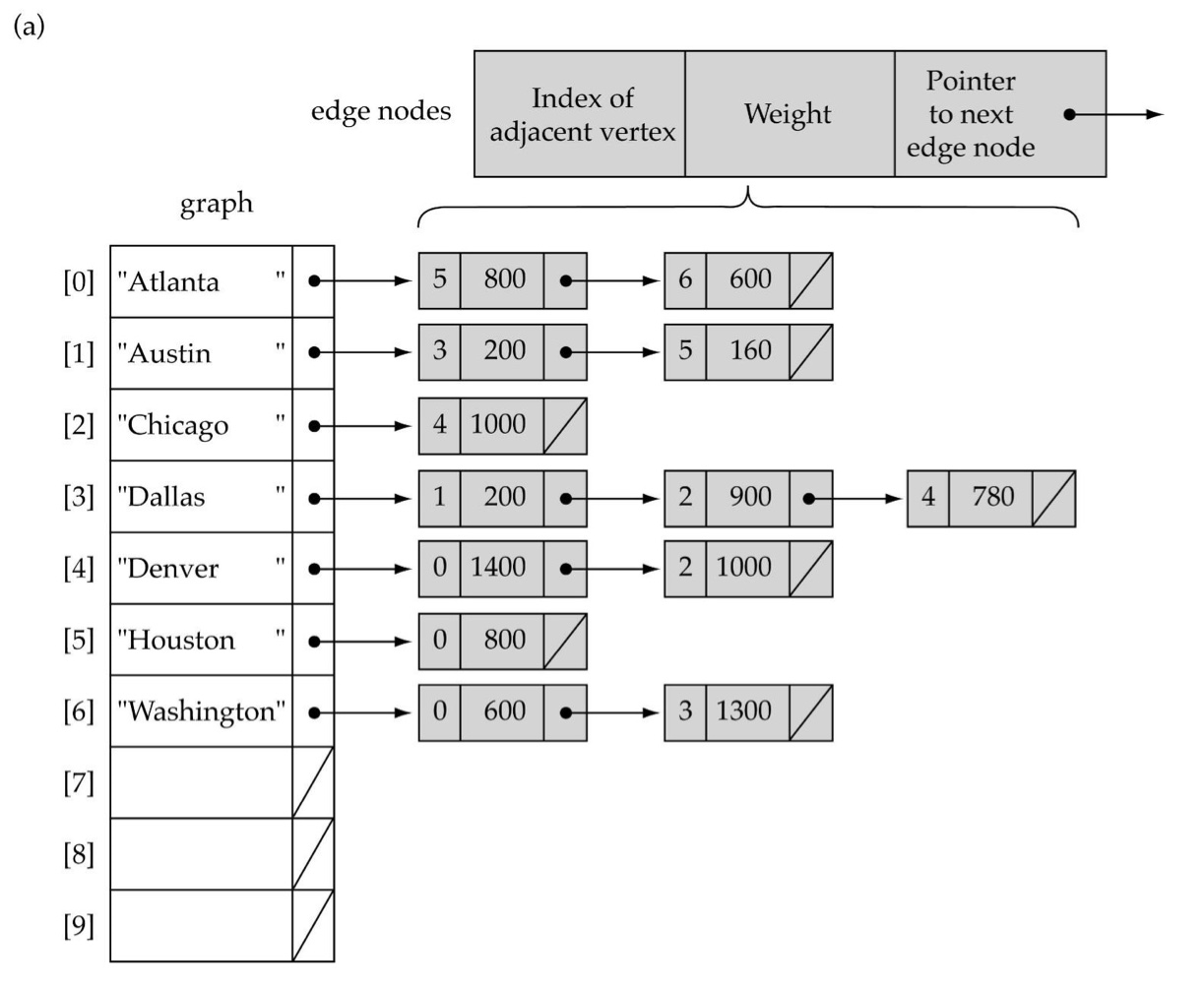
2. Adjacency List : Linked-list implementation

1D array is used to represent the vertices
List is used for each vertex V which contains the vertices which are adjacent from V
장점 : edge의 개수가 적을 때 좋다
단점 : overhead. Linked List 관리가 까다롭다. Undirected면 하나를 지울 때 양쪽에서 모두 지워야하는 데 이 구현이 귀찮다.

3. Array-based versus Linked-list

Implementation Code

1. Adjacencey Matrix

1-1. Class Declaration

const int NULL_EDGE=0;

template<classs VertexType>
class Graph
{
public:
	GraphType(int);
    ~GraphType();
    void MakeEmpty();
    bool IsEmpty() const;
    bool IsFull() const;
    void AddVertex(VertexType);
    void AddEdge(VertexType, VertexType, int);
    //             에서         로    이만큼 가중치 둬서 연결
    int WeightIs(VertexType, VertexType); // 가중치 Return
    void GetToVertices(VertexType, QueType<VertexType>&); 
    //                를 주고 계산해서     에다가 직접 연결되어있는 이웃 vertex를 저장
    void ClearMarks();
    // 지나가지 않았다고 false로 초기화
    void MarkVertex(VertexType);
    // 방문했다고 표기하는 함수 : IndexIs로
    bool IsMarked(VertexType) const;
    // 방문여부 확인하는 함수 : IndexIs로
private:
	int numVertices; // 지금 몇 개
    int maxVertices; // 최대 몇 개 
    VertexType* vertices;
    int** edges; // 2차원 array라서 pointer의 pointer
    bool* marks; // 지나갔다는 표시용
};

1-2. Constructor and Deconstructor

template<class VerTexType>
GraphType<VerTexType>::GraphType(int maxV) // param: 최대 개수 지정
{
	numVertices=0;
    maxVertices=maxV;
    vertics=new VertexType[maxV];
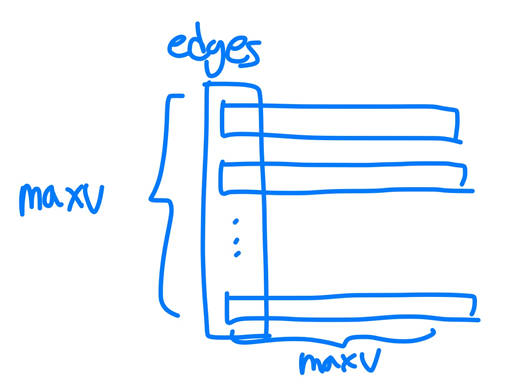
    edges=new int[maxV]
    for(int i=0; i<maxV; i++)
    	edges[i]=new int[maxV]; // [maxV][maxV]의 2D array가 완성된다.
    marks=new bool[maxV];
}

template<class VerTexType>
GraphType<VerTexType>::~GraphType()
{
	delete [] vertices;
    for(int i=; i<maxVertices; i++)
    	delete [] edges[i]; // 2차원 array 할당 삭제므로 edges[i]부터 지워야 한다는 것 주의
    delete [] edges;
    delete [] marks;
}

1-3. AddVertex & AddEdge

template<class VerTexType>
void GraphType<VerTexType>::AddVertex(VertexType vertex)
{
	vertices[numVertices]=vertex; // 1D array에 assign한다.
    for(int index=0; index<numVertices; index++)
    {
    	edges[numVertices][index]=NULL_EDGE; // 0으로 initialize
        edges[index][numVertices]=NULL_EDGE; // 0으로 initialize
    }
    numVertices++;
}

template<class VerTexType>
void GraphType<VertexType>::AddEdge(VertexType from Vertex, VertexType toVertex, int weight)
{
	int row;
    int column;
    //           리스트        이름
    row=IndexIs(vertices, fromVertex); // 인덱스 구해서 알려줘 
    col=IndexIs(vertices, toVertex);
    edges[row][col]=weight;
}

1-4. WeightIs

template<class VerTexType>
int GraphType<VerTexType>::WeightIs(VertexType fromVertex, VertexType toVertex)
{
	int row;
    int col;
    
    row=IndexIs(vertices, fromVertex);
    col=IndexIs(vertices, toVertex);
    return edges[row][col];
}

Graph Searching

Problem : 그래프의 두 노드 사이의 경로를 찾고싶다. -> 모든 노드를 방문(traverse)하는 방법 있어야 한다.
방법 : Depth-First-Search(DFS) or Breadth-First-Search(BFS)

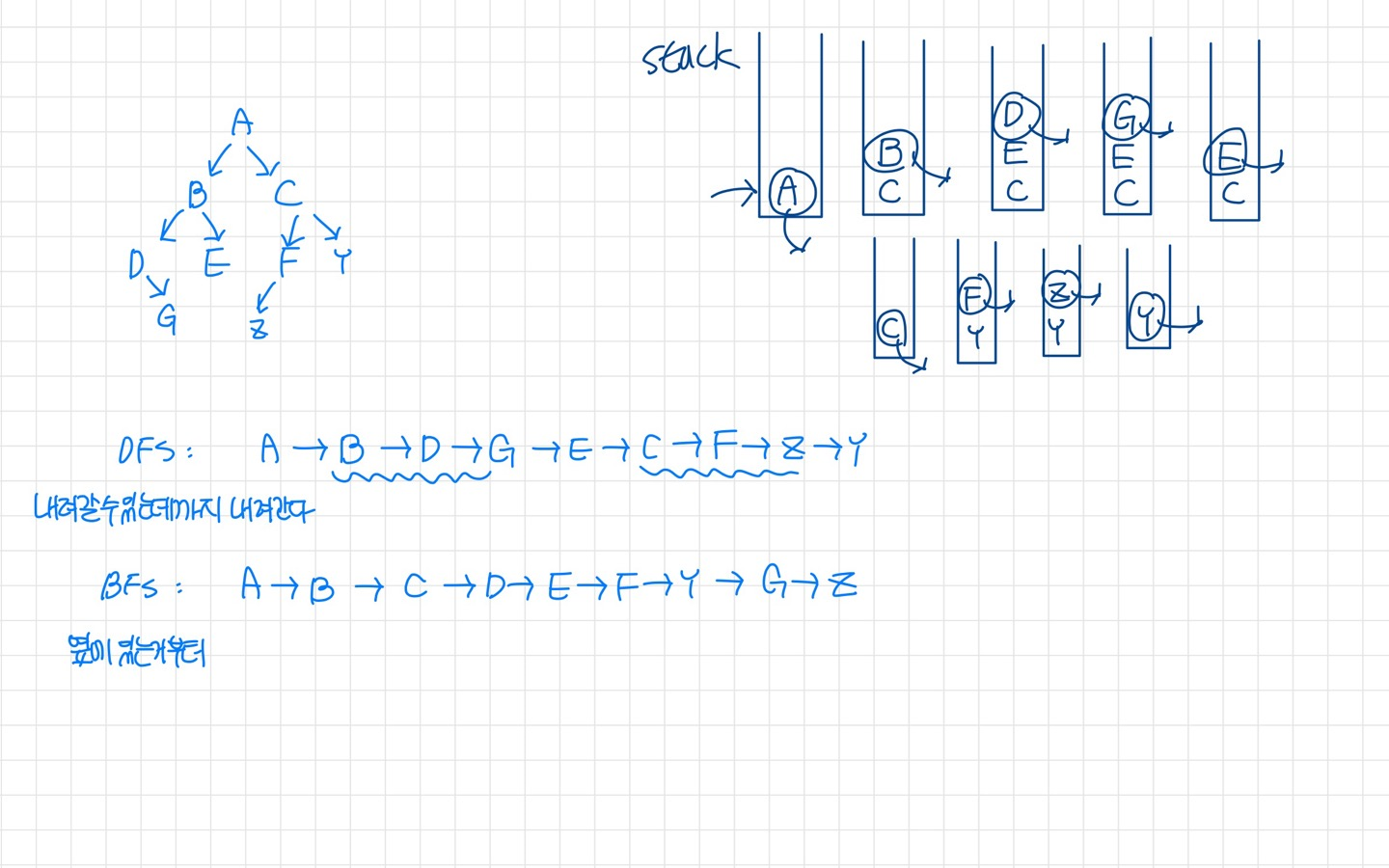
1. Depth-First-Searh (DFS)

올라가기 전에 가장 깊은 곳까지 내려간다, 가능한 멀리 간다.(to its deepest point, as far as you can)
DFS는 Stack을 사용하면 효율적으로 구현할 수 있다.

📘 DFS 메커니즘 📘

Set found to false

stack.Push(startVertex)

Do
{
stack.Pop(vertex)
If vertex == endVertex : set Found to True
ELSE: Push all adjacent vertices onto stack
}
WHILE (!stack.IsEmpty() && !found )

If (!found)
Write "Path does not Exit"

Austin을 Push한 stack에서 Austin을 Pop하면서 Dallas와 Houston을 Push한다.
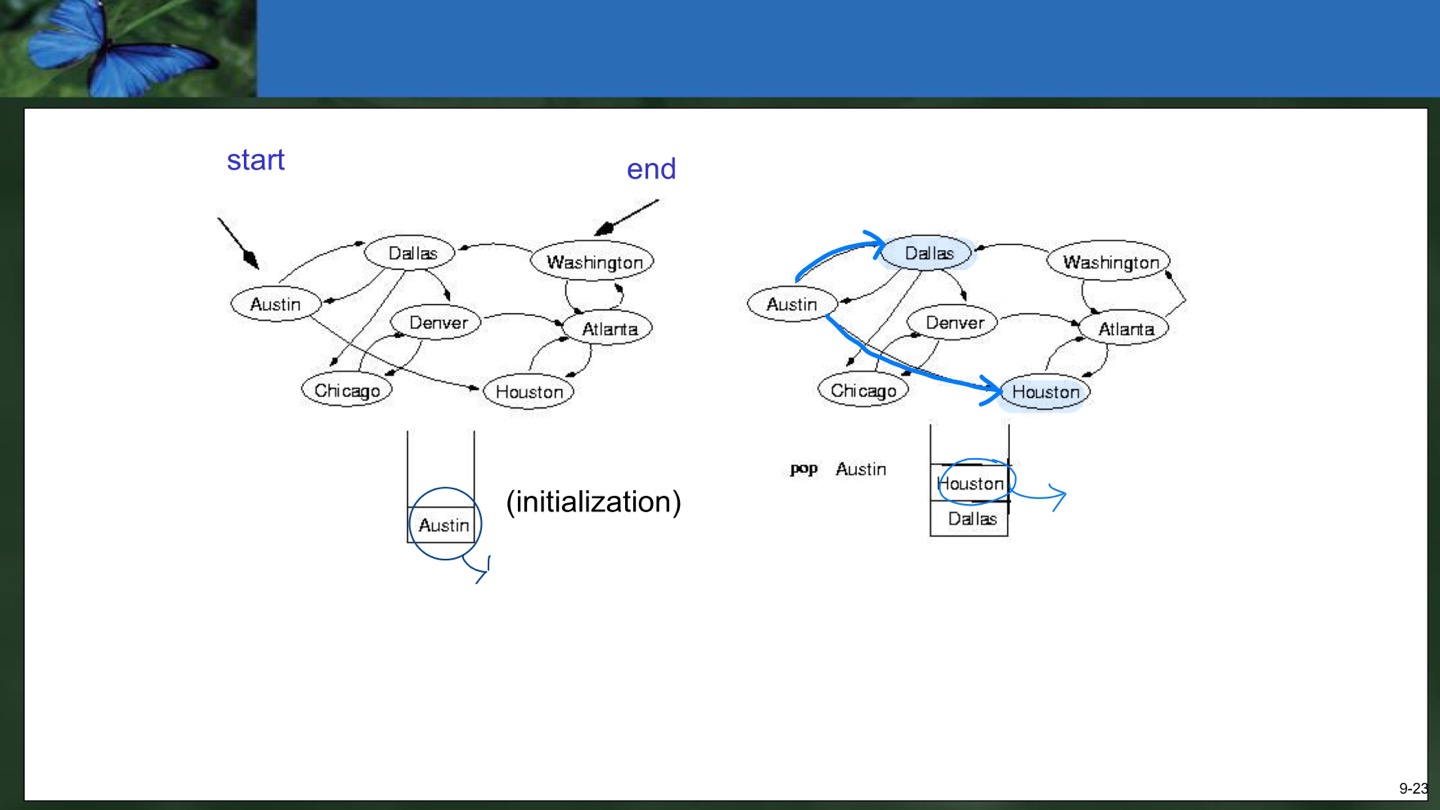2. Houston을 Pop하면서 Atlanta를 Push한다. 3. Atlanta를 Pop하면서 Wasington을 Push한다. 이때 Houston은 이미 Pop된 적이 있으므로 marking이 되어있기 때문에 Push하지 않는다. 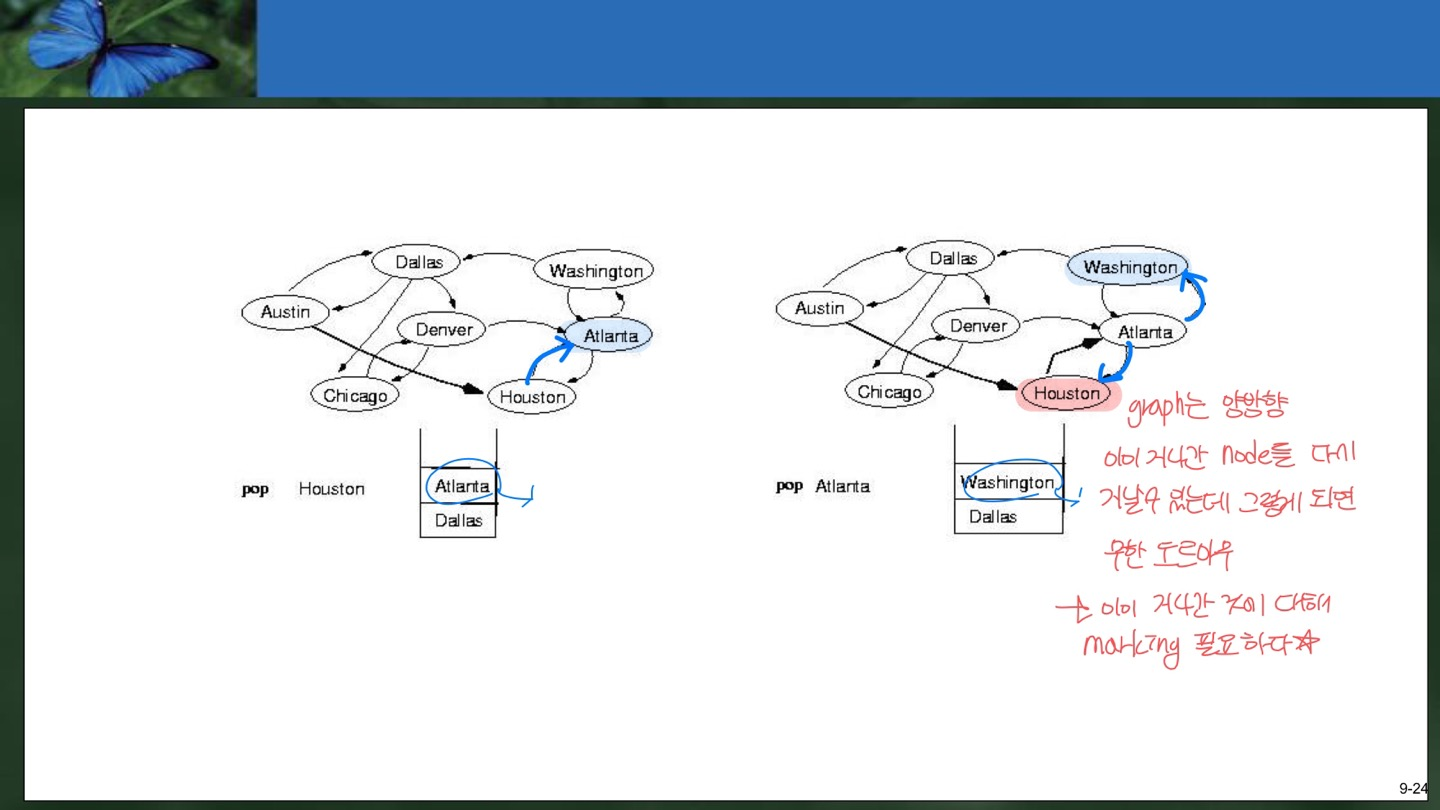4. Washington을 Pop하고 끝난다. found=true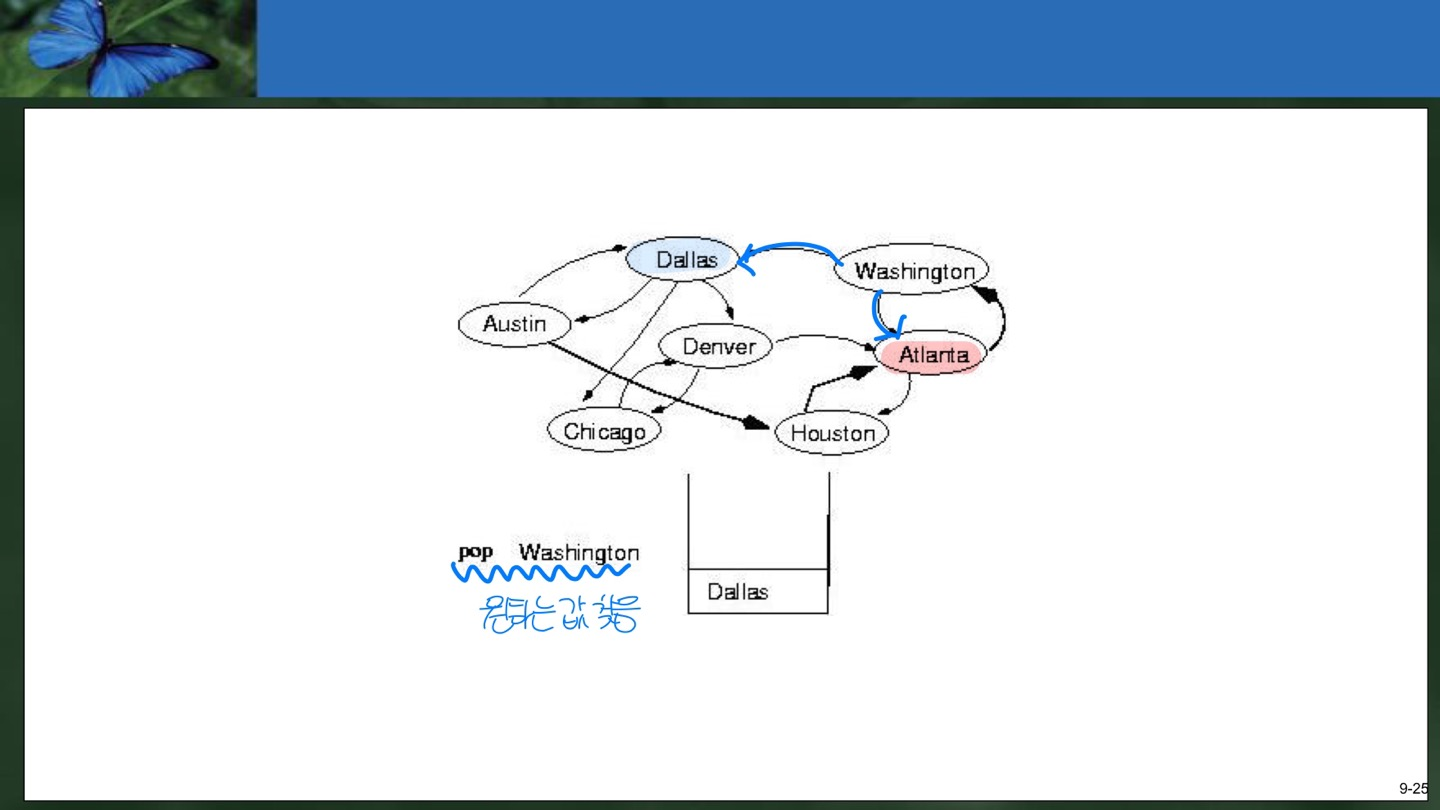

DFS IMPLEMENTATION

template<class ItemType>
void DepthFirstSearch(GraphType<VertexType> graph, VertexType startVertex, VertexType endVertex)
{
	StackType<VertexType> stack;
    QueType<VertexType> vertexQ;
    
    bool found=false;
    VertexType vertex;
    VertexType item;
    
    graph.ClearMarks(); // 아직 어떤 vertex도 방문하지 않았으므로 mark를 모두 fasle로 초기화해준다. 
    stack.Push(startVertex); // 출발 vertex를 stack에 넣는다. 
    do
    {
    	stack.Pop(vertex); // 가장 위에 있는 vertex를 꺼낸다.
        if(vertex==endVertex) // 만약 pop 한 vertex가 우리가 찾는 vertex라면
        	found=true; // 끝낸다. 
        else  // pop한 vertex가 우리가 찾는 vertex가 아니라면
        {
        	// Q. 이 graph.IsMarked(vertex)는 확인할 필요가 있을까? 없을지도
        	if(!graph.IsMarked(vertex) ) // 우리가 이미 방문했던 vertex가 아니라면
            {
            	graph.MarkVertex(vertex); // 방문했다고 Mark를 찍어준다.
                graph.GetToVertices(vertex, vertexQ); // vertex의 이웃 vertex를 확인해서 Queue에 저장한다.
                
                while (!vertexQue.IsEmpty() ) // 모든 이웃 vertex들에 대해. Q 빌때까지
                {
                	vertexQ.Dequeue(item); // 꺼낸다.
                    if(!graph.IsMarked(item)) // 이웃 vertex에 mark 찍혀있는지 확인한다.
                    	stack.Push(item); // mark 찍혀있지 않은 이웃 vertex를 stack에 추가한다.
                 }
            }
     } while (!stack.IsEmpty() && !found); // stack이 비거나(끝까지 내려감) 찾으면 종료
     
     if(!found) // 끝까지 돌았는데 없으면 경로가 존재하지 않는 것이다. 
     	cout<<"Path not found"<<endl;
    }

template<class VertexType>
void GraphType<VertexType>::GetToVertices(VertexType vertex, QueType<VertexTYpe>& adjvertexQ)
{
	int fromIndex;
    int toIndex;
    
    fromIndex=IndexIs(vertices, vertex); // 현재 vertex의 인덱스값을 받는다.
    for(toIndex=0; toIndex<numVertices; toIndex++) // 0부터 numV까지
    {
    	if (edges[fromIndex][toIndex] != NULL_EDGE ) // 0이 아닌 애들을 찾아서
        	adjvertexQ.Enqueue(vertices[toIndex]); // 넣는다.
}

2. Breadth-First-Searching (BFS)

visit all the nodes on one level before going to the next level
Look at all possible paths at the same depth before you go at a deeper level

📘 BFS 메커니즘 : Queue를 통해 구현 📘
1) Set found to false
2) queue.Enqueue(startVertex)
3) Do
{
queue.Dequeue(vertex)
IF vertex == endVertex : set found to true
ELSE : Enqueue all adjacent vertices onto queue
}
WHILE ( !queue.IsEmpty() && !found)
4) IF (!found)
Write "Path does not exist"

1) Ausitn을 Queue에 넣는다. 2) Austin을 Dequeue하고 Dallas와 Houston을 Enqueue한다.
3) Dallas를 Dequeue하고 이미 방문한 Austin을 제외한 Chicago와 Derver를 Enqueue한다.
4) Houston을 Dequeue하고 Atlanta를 Enqueue한다.

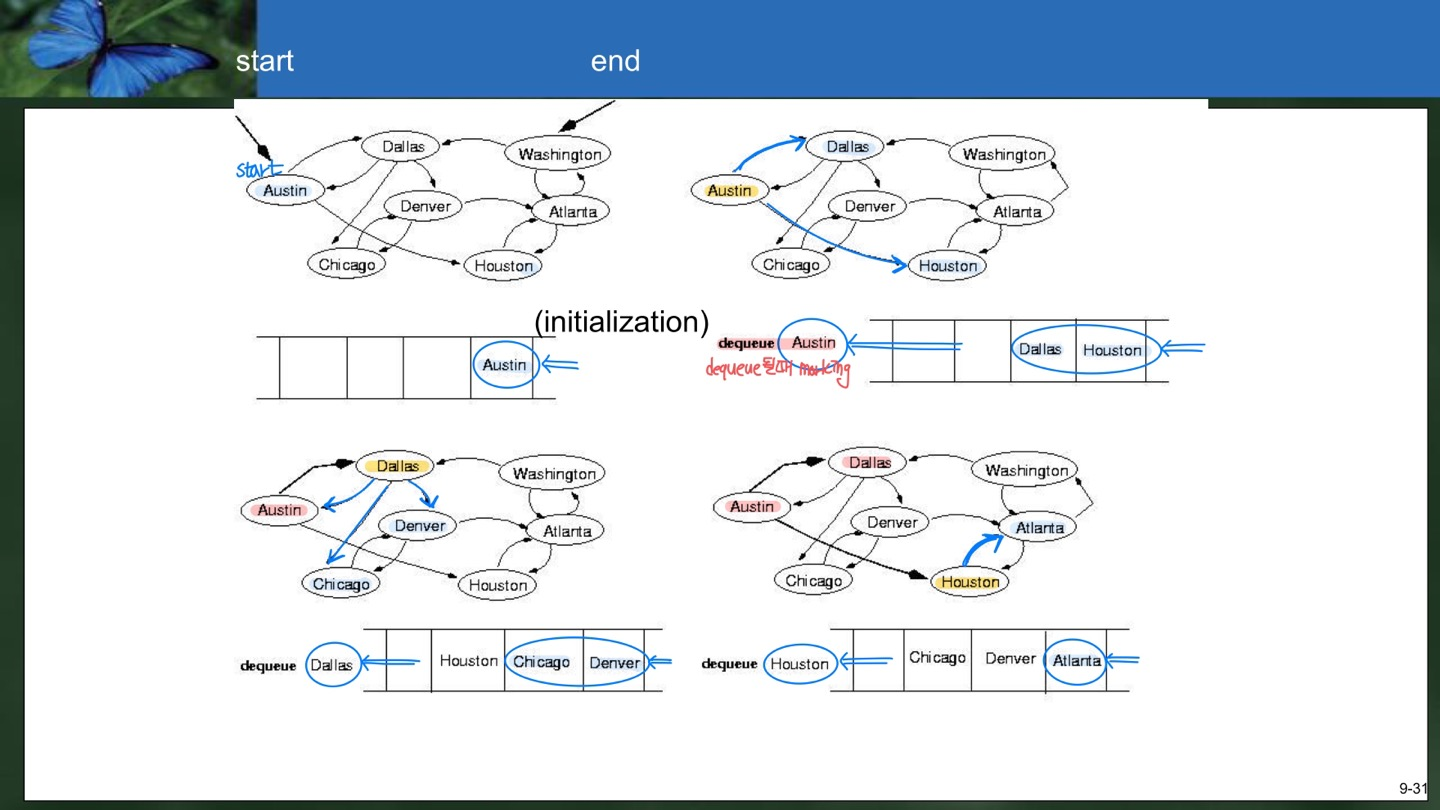
5) Chicago를 Dequeue하고 Derver를 Enqueue한다. 이때 Derver가 Queue에 중복 존재하는데 이는 우리가 Dequeue할 때 Marking을 하는데 Derver가 아직 Dequeue되지 않았기 때문이다.
6) Derver를 Dequeue하고 이미 방문한 Chicago를 제외한 Atlanta를 Enqueue한다. 이때 역시 Queue에 Atlanta가 중복되게 존재하는 상황이 발생한다.
7) Atlanta를 Dequeue하고 이미 방문한 Houston을 제외한 Washington을 Enqueue한다.
8) Derver를 Dequeue하는데 Derver의 모든 이웃 노드가 marking되어있으므로 어떤 것도 Enqueue하지 않는다.
9) Atlanta를 Dequeue하고 이미 방문한 Houston을 제외한 Washington을 Enqueue한다. 이때 역시 Queue에 Washington이 중복하여 존재한다.

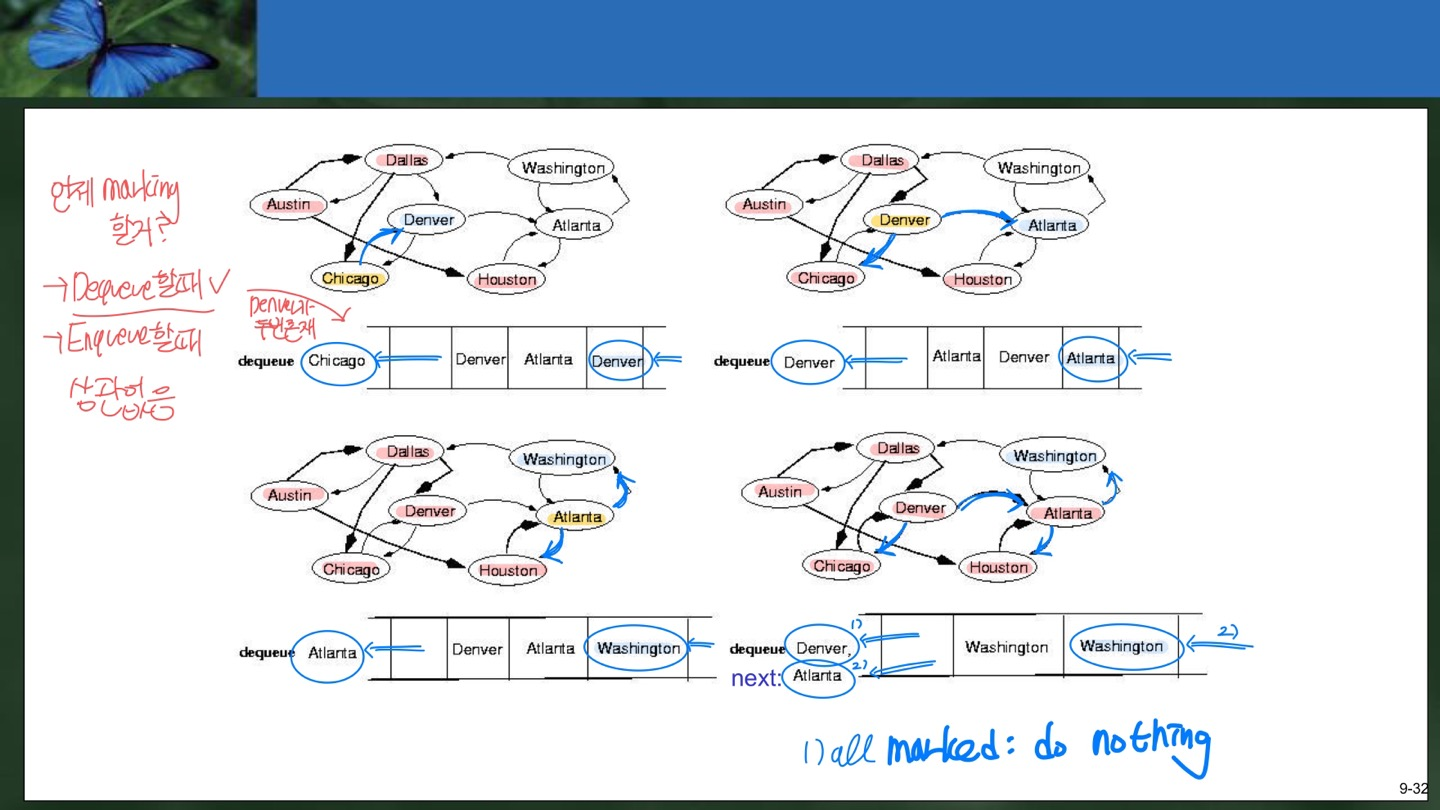
10) Washington을 Dequeue한다. 우리가 원하는 Washington을 찾았으므로 종료한다.

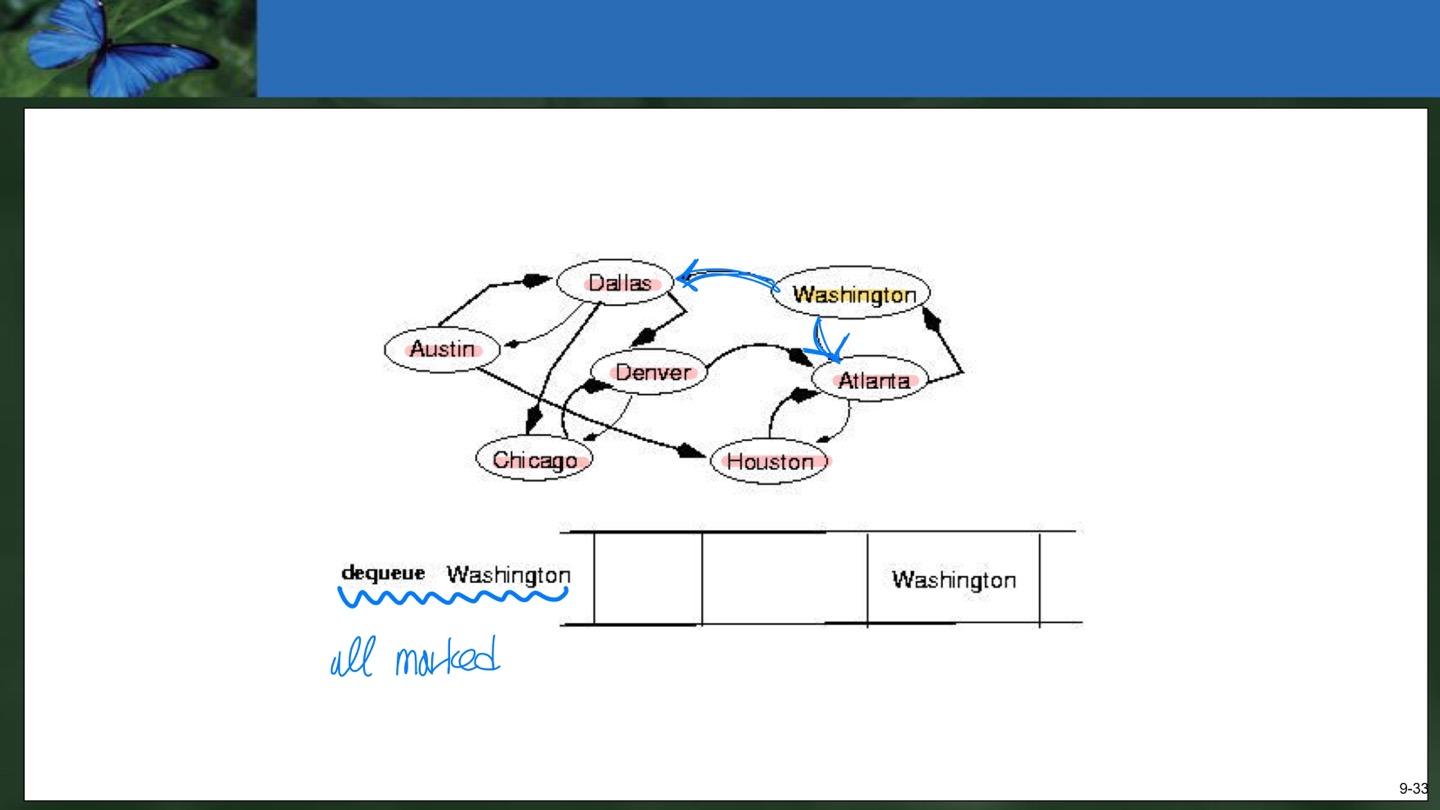
BFS Implementation

template<class VertexType>
void BreadthFirstSearch(GraphType<VertexType> graph, VertexType startVertex, VertexType endVertex)
{
	QueType<VertexType> queue;
    QueType<VertexType> vertexQ;
    
    bool found=false;
    VertexType vertex;
    VertexType item;
    
    graph.ClearMarks();
    queue.Enqueue(startVertex);
    do {
    	queue.Dequeue(vertex);
        if(vertex==endVertex)
        	found=true;
        else
        {
        	// 현재 vertex가 방문했던 vertex인지 확인 -> 이것도 반드시 필요한가?
        	if(!graph.IsMarked(vertex))
            {
            	graph.MarkVertex(vertex);
                graph.GetToVertices(vertex, vertexQ);;
                
                while (!vertexQ.IsEmpty() )
                {
                	vertexQ.Dequeue(item); // vertex Queue에서 꺼내와서
                    if (!graph.IsMarked(item))
                    	queue.Enqueue(item); // candidate 관리 Queue에 집어넣는다.
                }
            }
        }
       } while (!queue.IsEmpty() && !found);
       
       if(!found)
       	cout<<"Path not found"<<endl;
}

Single-source shortest-path problem

Shortest path : the path whose total weight (= sum of edge weights) is minimum
=> Dijkstra's algorithm, Bellman-Ford algorithm
BFS는 Weightless (가중치가 없거나 모든 가중치가 동일한 경우) Graph인 경우 shortest path problem을 풀 수 있다.

Set (집합)

Base Type
: The type of the items in the set

Cardinality
: The number of items in a set

Cardinality of the base type
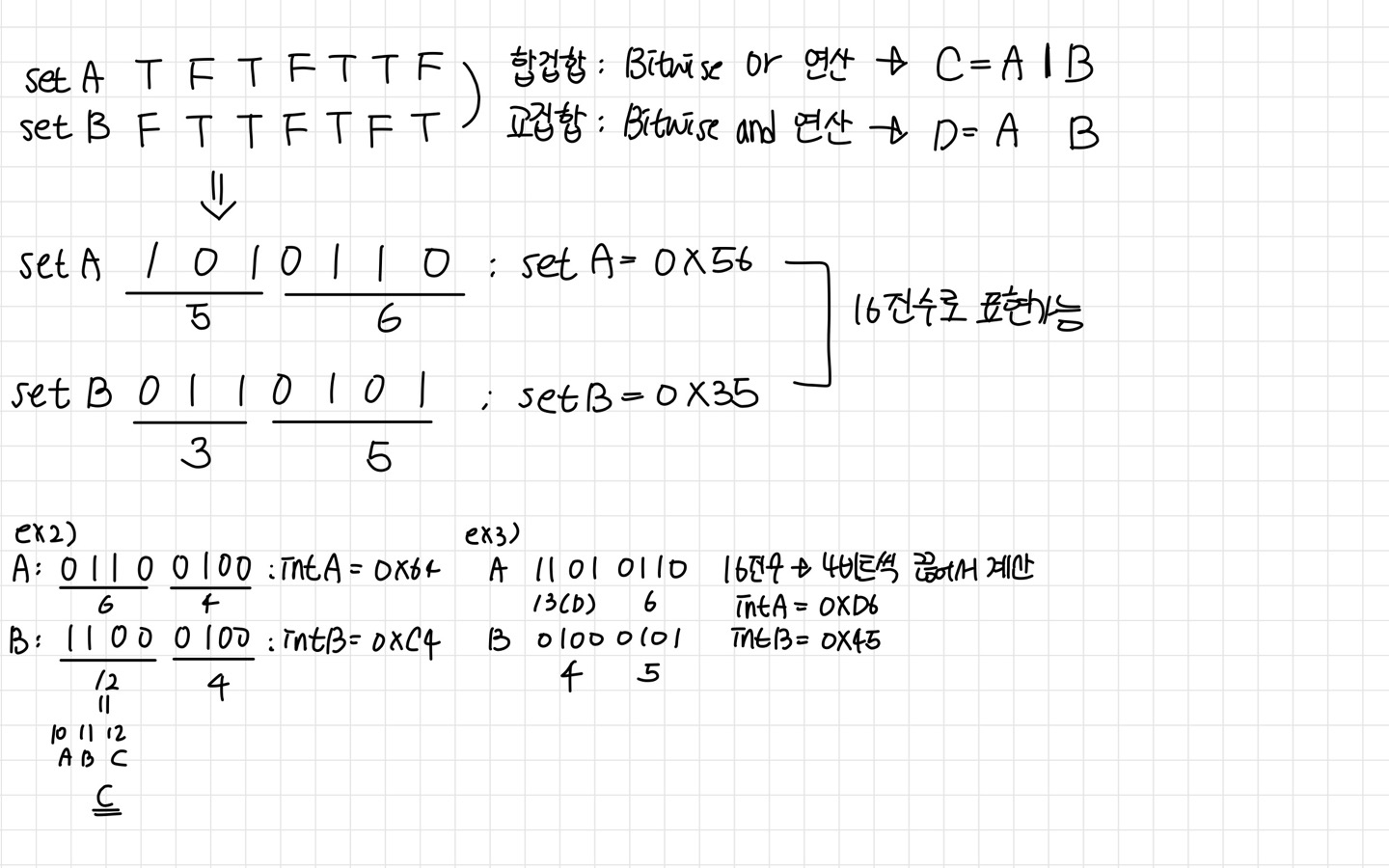
: The number of items in the base type

Union of two sets (합집합)
: A set made up of all the itmes in either sets

Intersection of two sets (교집합)
: A set made up of all the items in both sets

Difference of two sets (차집합)
: A set made up of all the itmes in the first set that are not in the second set