[자료구조] Chapter 7. Programming with Recursion

nothingisme·2022년 11월 21일

[자료구조]

목록 보기

1/6

0. 개념

Recursive Call : A Method call in which the method being called is the same as the one making the call (=자기 자신을 호출하는 메소드)

Direct 는 f->f 형태, Indirect는 f->g->f 형태이다.
단점 : 무한 루프에 빠질 수 있다, iterative(반복문)보다 덜 효율적(실행속도, 메모리)일 수 있다.
장점 : simple & elegant. 간단하므로 프로그램 읽기가 쉽다(readability 향상). 따라서 소스 코드 관리 비용을 절감할 수 있다.

1. 원칙 : Divide and Conquer

recursive의 가장 큰 원칙은 문제를 쪼개서 풀고 확인하는 작업을 반복하는 것이다.

Base case: recursive call을 언제 끝낼지에 대한 조건을 명시해준다. 반드시 존재해야 한다.
General(recursive) case : 더 작게 쪼개지는. 재귀 호출 상황.

if (some condition for which answer is knonw) // base case
	solution statement
else // general case
	recursive function call

2. Factorial Recursion Function : 팩토리얼 재귀 함수

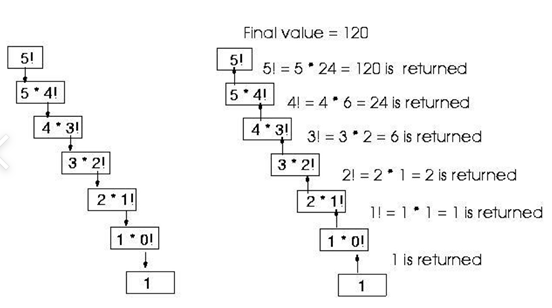
n! = n * (n-1)! 이므로 재귀로 표현될 수 있다.
재귀를 반복하다가 1!=1 x 0!에 이르면 0!일 때가 base case로 재귀 호출을 종료하면 된다.

int Factorial(int number)
// Pre: number is assigned and number>=0.
{
	if(number==0) // base case
    	return 1;
    else         // general case
    	return number*Factorial(number-1);
}

3. Combination Recursion Function : 조합 재귀 함수

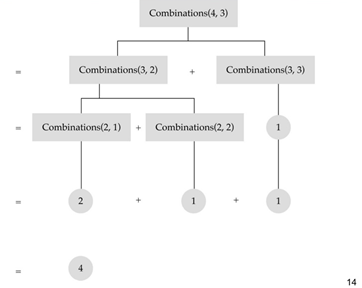
nCk = n-1Ck + n-1Ck-1 로 나타낼 수 있으므로 재귀로 표현될 수 있다.

Base case 1 : nC1=n ( k==1 )
Base case 2 : nCn=1 ( k==n )

int Combinations(int n, int k)
{
	if(k==1) // base case 1
    	return n;
    else if (n==k) // base case 2
    	return 1;
    else 
    	return (Combinations(n-1, k)+Combinations(n-1,k-1));
}

4. 재귀 함수 검증하는 3가지 방법

5. x의 n승을 재귀 함수로 표현하기

x^n = x * x^n-1이므로 n제곱승은 재귀 함수로 표현될 수 있다.
x^0=1일 때가 base case가 된다.

int Power(int x, int n)
// Pre : n>=0. x, n are not both zero.
// Post : Function value = x raised to the power n.
{
	if(n==0) // base case
    	reutnr 1;
    else // general case
    	return (x*Power(x,n-1));

6. struct ListType ValueInList 함수

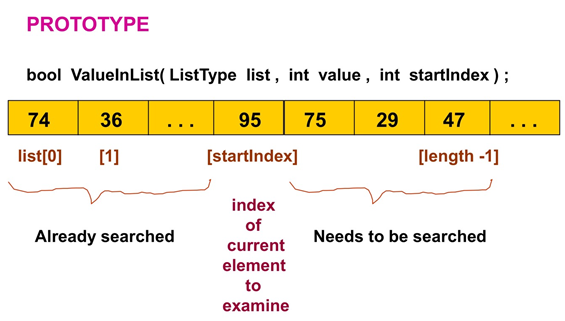
struct type의 List에서 값을 찾는 함수를 재귀 함수로 구현한다.
기존에는 length-1 까지 iteration을 하는 형태로 구현했다.
이제 시작 인덱스를 Parameter로 받는다.
찾았을 때와 끝까지 갔을 때(마지막까지 확인했는데 없을 때)가 Base case가 된다.
만약 Base case에 해당하지 않으면 다음 칸(startIndex+1)부터 시작하는 재귀 함수를 호출하는 General case가 된다.

struct ListType
{
	int length; // number of elements in the list.
    int info[MAX_ITMES];
 };
 
 ListType list;
 
 bool ValueInList(ListType list, int value, int startIndex)
 {
 	if (list.info[startIndex] == value) // base case 1
    	return true;
    else if (startIndex == list.length-1) // base case 2
    	return false;
    else                                // general case
    	return ValueInList(list, value, startIndex+1);

7. struct ListType RevPrint 함수

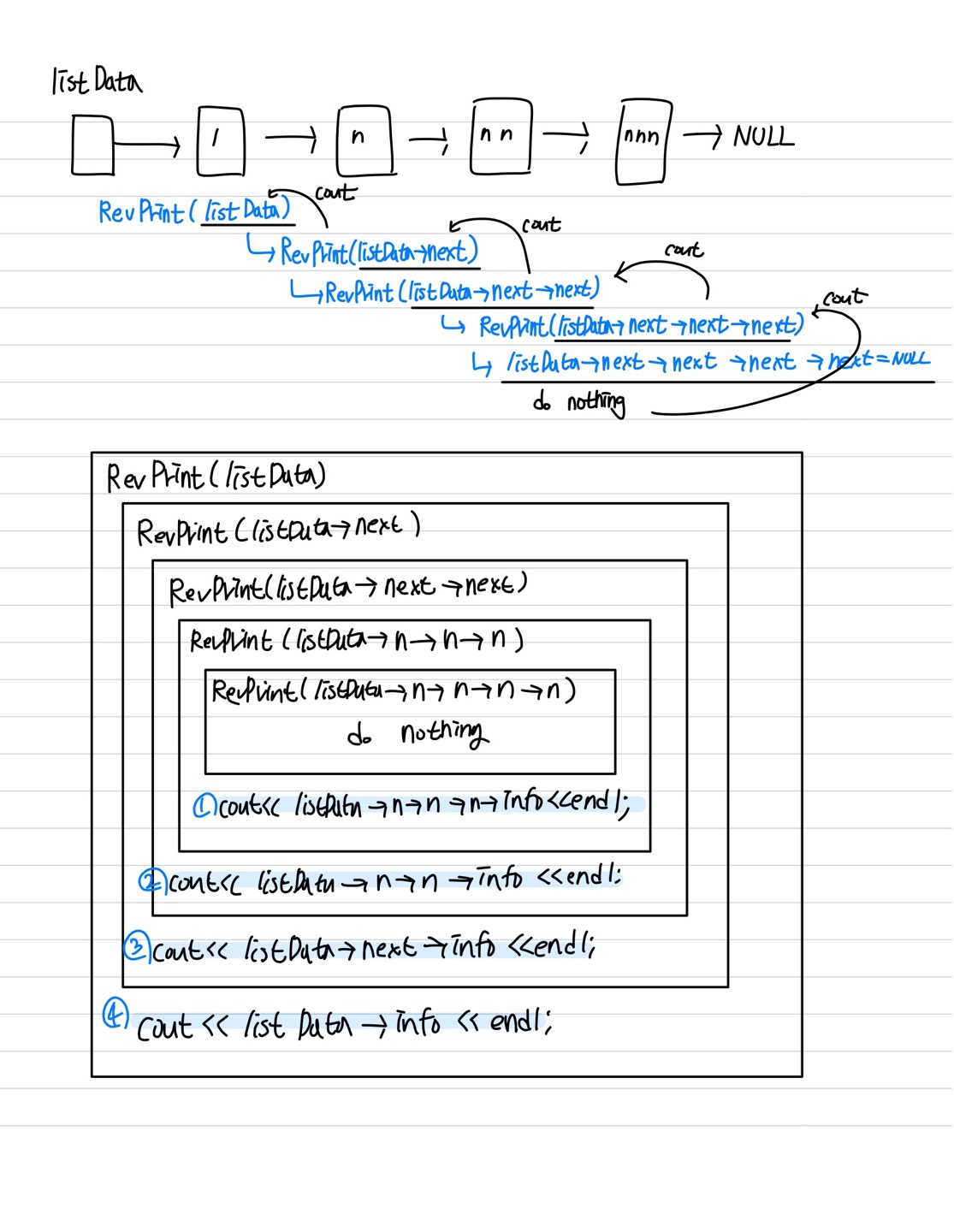
제일 뒤로 간 다음, 나오면서 Print를 하면 역순으로 출력이 된다. 일반적과 달리
재귀호출을 한 다음 Print를 하는 방식이다.

struct NodeType
{
	int info;
    NodeType* next;
}

class SortedType
{
public:

private:
	NodeType* listData;
};

void RevPrint(NodeType* listPtr)
{
	if(listPtr!=NULL) // general case
    {
    	RevPrint(listPtr->next);
        std::cout<<listPtr->info<<std::endl; //print this element
    }
    // base case : if the list is empty, do nothing
}

8. BinarySearch() Recursion Function

// Non Recursive Implementaion
template<class ItemType>
void SortedType<ItemType>::RetrieveItem(ItemType& item, bool& found)
{
	int midPoint;
    int first=0;
    int last=length-1;
    
    found false;
    while( (first<=last) && !found ) 
     {
    	midPoint = (first+last)/2;
        if (item<info[midPoint])
        	last=midPoint-1;
        else if (item>info[midPoint])
        	first=midPoint+1;
        else 
        {
        	found=true;
            item=info[midPoint]
        }
    }
  }

Recursive Binart Search

size factor : the number of elements in ( info[first] ... info[last] )

base case
(1) If first > last, return false
끝까지 갔는데 찾지 못했으면 false 반환하고 종료
(2) if item==info[midPoint], return true
아이템의 위치를 찾으면 true 반환하고 종료

general case
(1) If item < info[midPoint] , search the first half
찾으려고 하는 값이 중간값보다 작으면 앞을 살핀다.
(2) If item > info[midPoint] , search the second half
찾으려고 하는 값이 중간값보다 크면 뒤를 살핀다.

// Recursive Implementation
template<class ItemType>
bool BinarySearch(ItmeType info[], ItemType item, int fromLoc, int toLoc) // 양쪽 끝을 param으로 받음
{
	int mid;
    if ( fromLoc > toLoc ) // base case-끝까지 갔는데 없는 경우. false 반환 후 종료.
    	return false;
    else
    {
    	mid=(fromLoc+toLoc)/2;
        if(info[mid]==item) // base case-찾은 경우. true 반환 후 종료.
        	return true;
        else if (item<info[mid]) // 작은 경우 앞부분
        	return BinarySearch(info, item, fromLoc, mid-1);
        else // 큰 경우 뒷부분
        	return BinarySearch(info, item, mid+1, toLoc);
    }
}

9. 함수 호출될 떄 Runtime Stack

함수의 코드에서 블럭(block)을 호출하는 것으로부터 통제(control)의 전환(transfer)이 발생한다. 함수 코드가 실행된 이후에 호출하는 블럭에서 올바른 위치로 반환(return)하는 것이 필요하다. 이 올바른 위치를 반환 주소(return address)라 부른다
어떤 함수가 호출될 때 runtime stack이 사용된다. 함수 호출에서 activation record(stack frame)가 이 스택에 쌓인다.
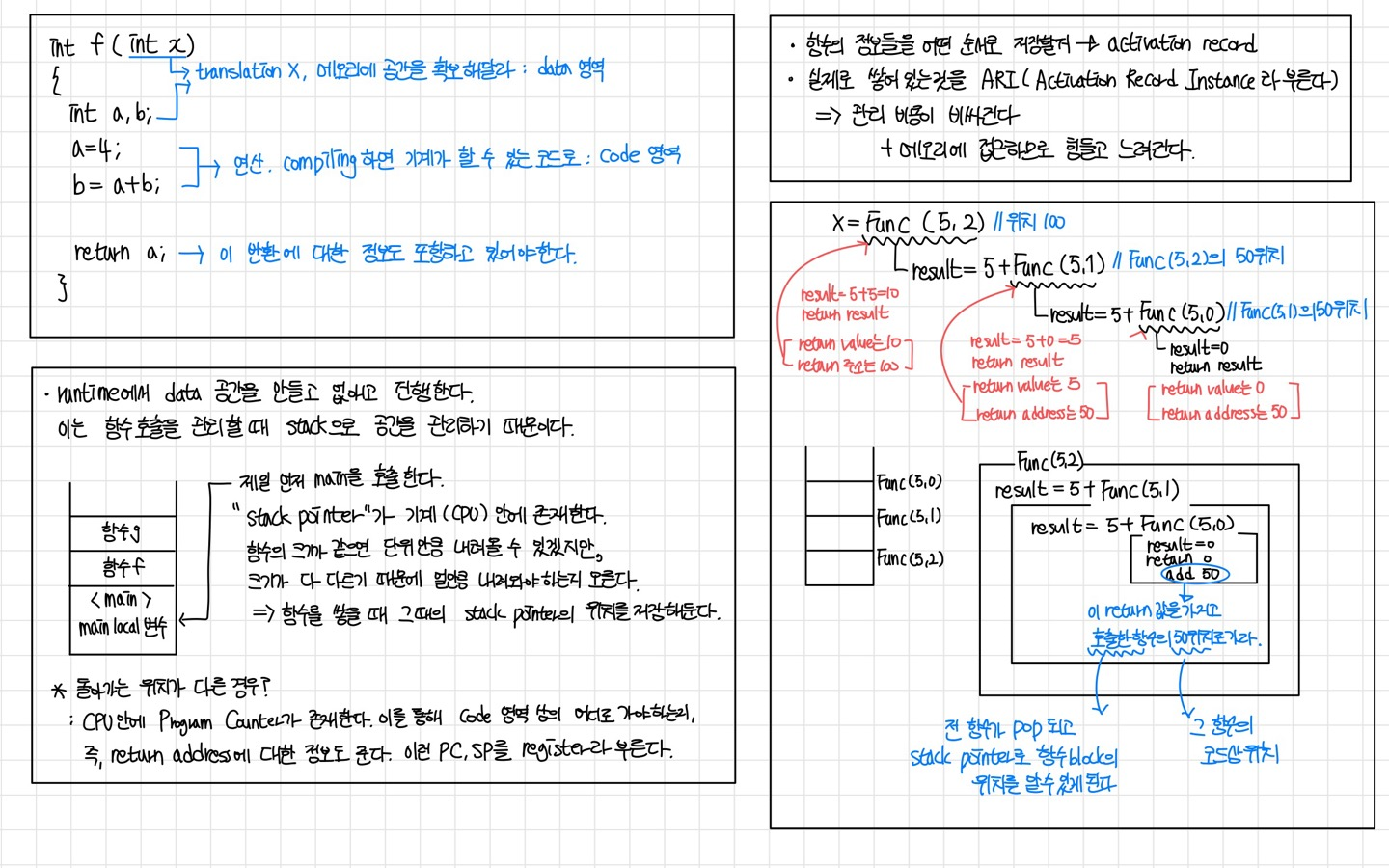
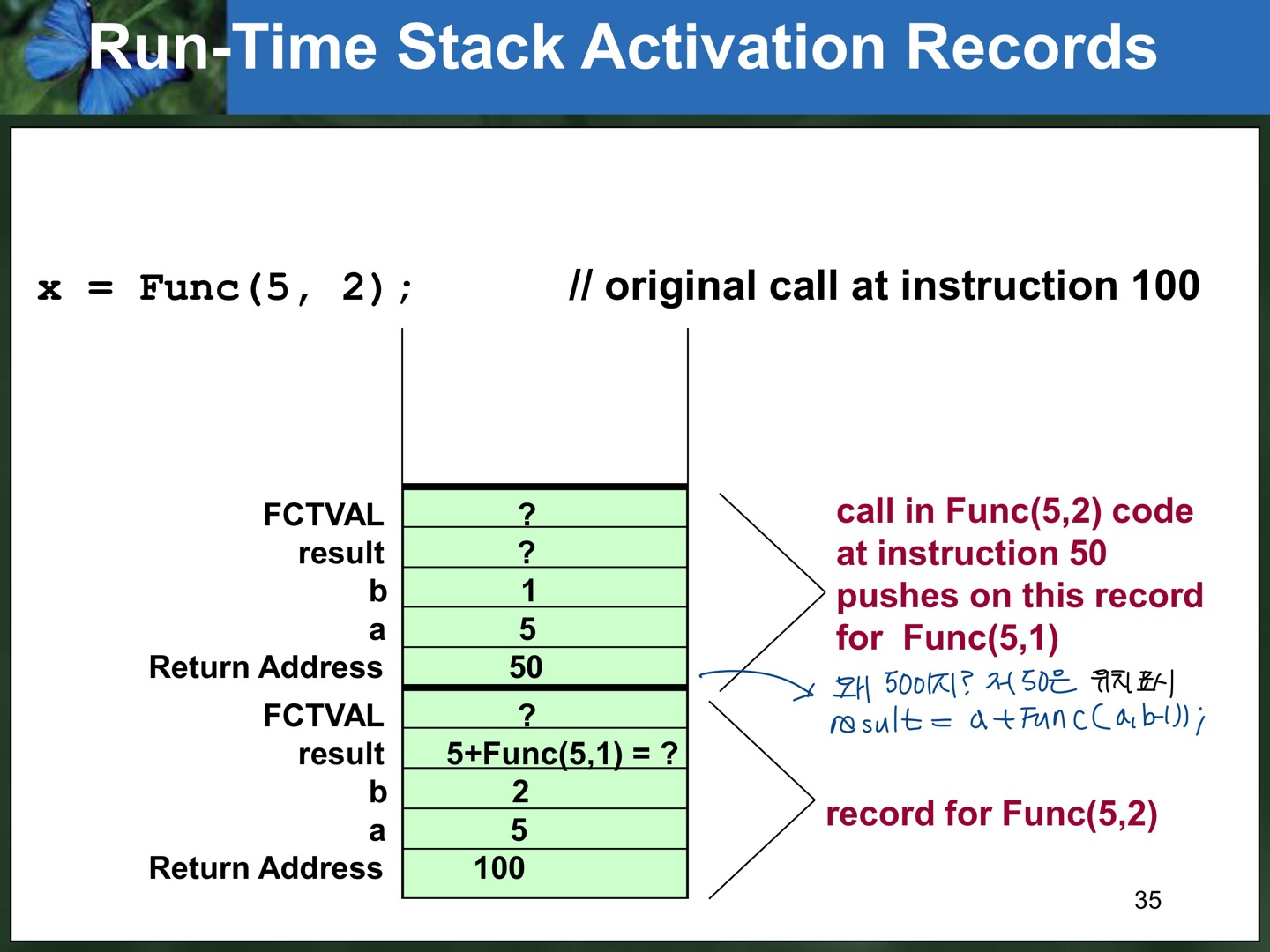
activation record는 이 함수 호출에 대한 return address와 함께 입력 parameter, 지역 변수, (void 아닐 경우) 함수의 반환 값에 대해 저장한다.
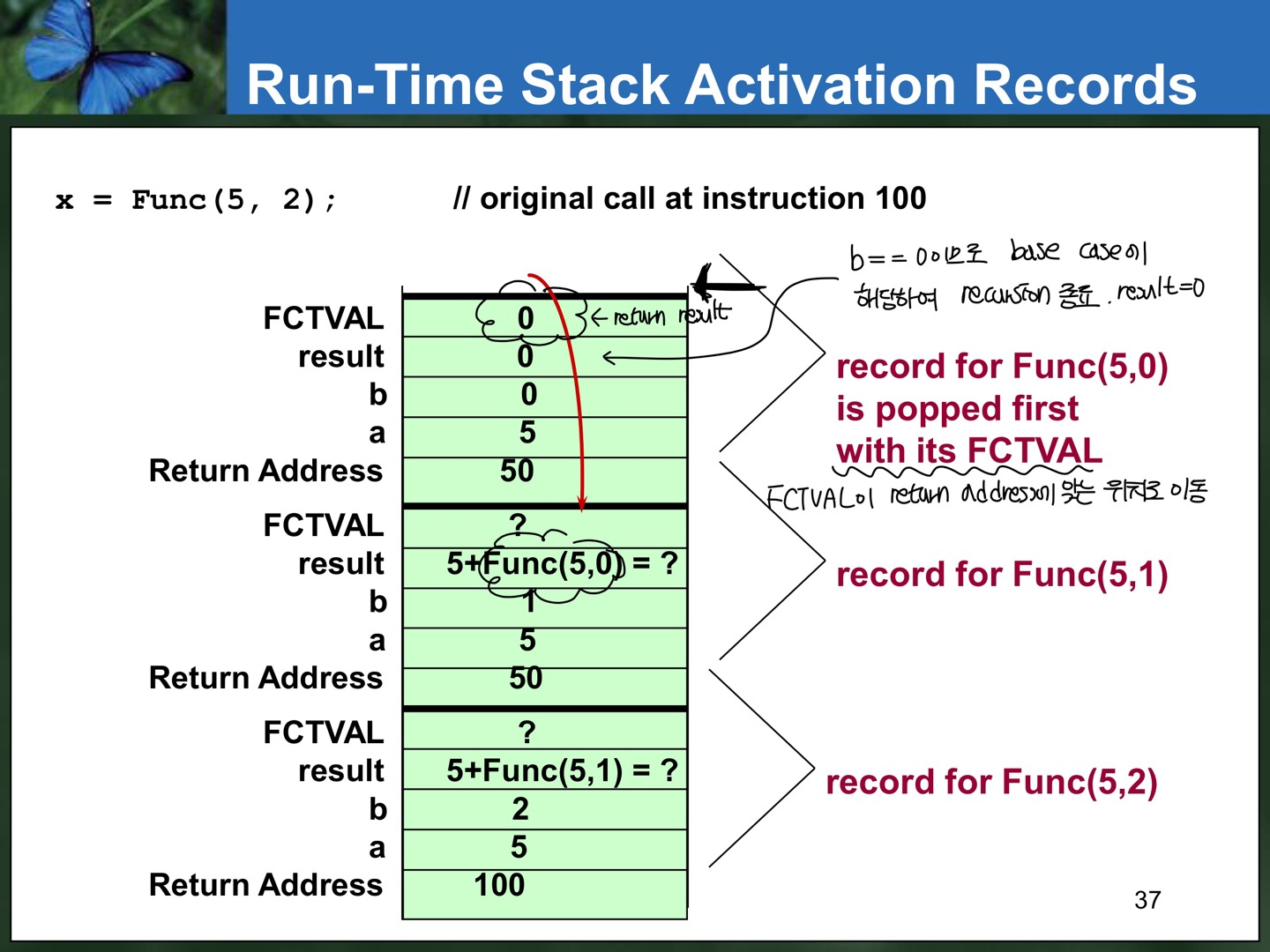
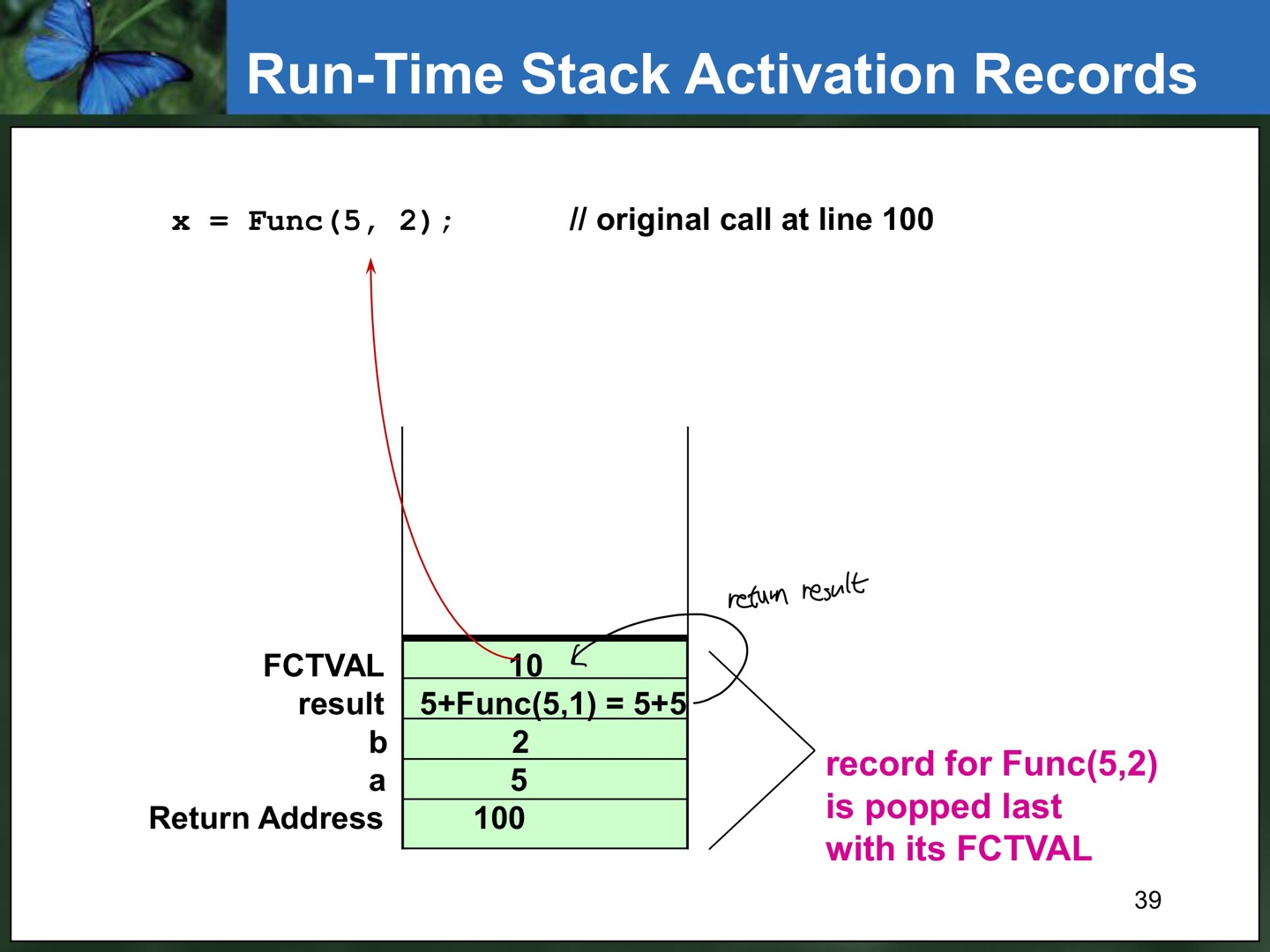
함수 코드의 마지막 닫는 괄호에 도달하거나 함수 코드에서 return statement에 도달한 경우, 특정 함수 호출에 대한 activation record는 runtime stack에서 pop되어서 나간다.
이때 void가 아니라면 그 함수의 반환값은 거기에 쓰인 반환 주소 호출 블럭으로 가져와진다.

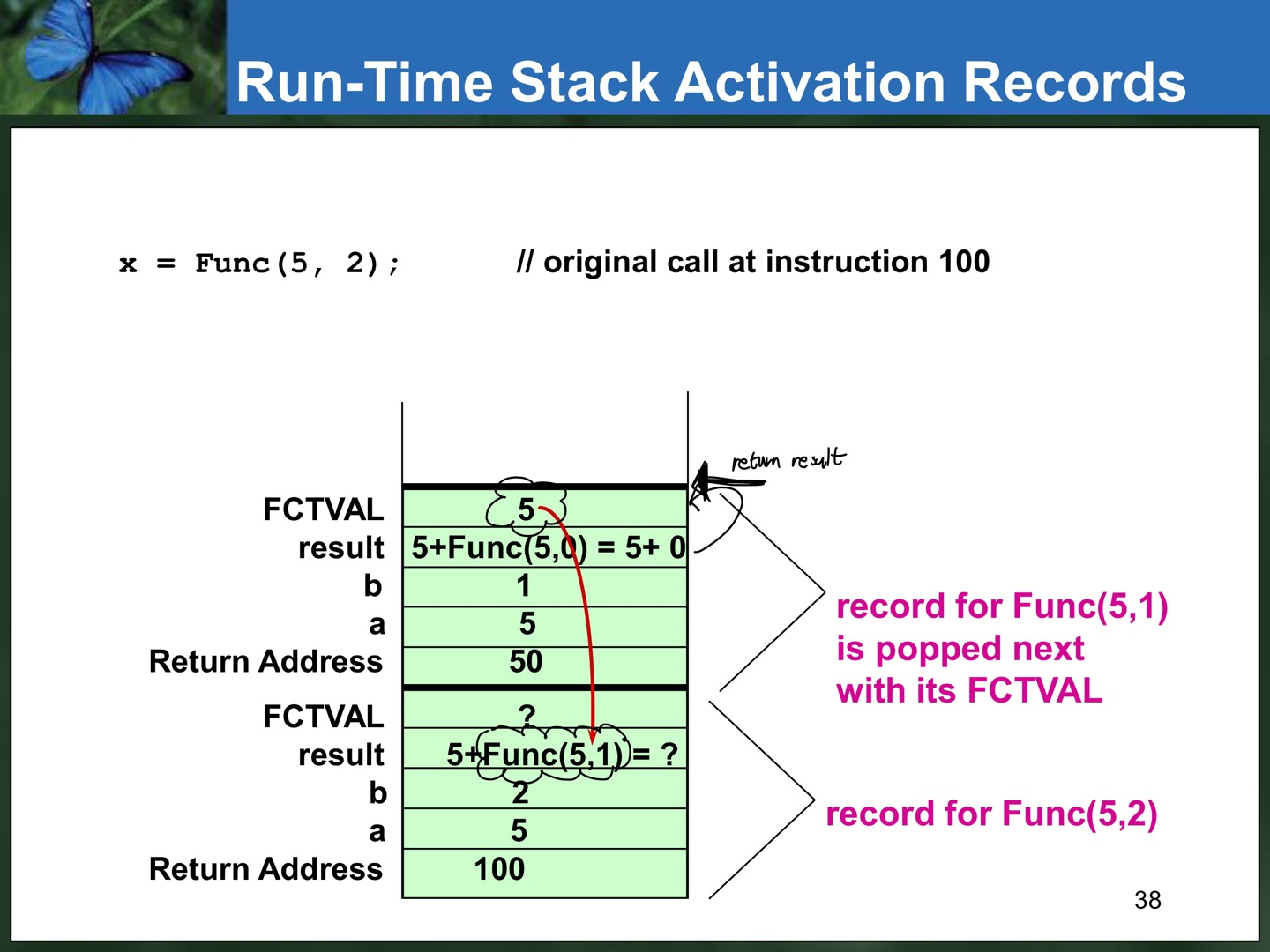
// Another recursive function
// instruction : 코드 상 위치를 명시
int Func(int a, int b) // instruction 100
{
	int result;
    if (b==0) // base case
    	result=0;
    else if (b>0) // general case1
    	result=a+Func(a,b-1); // instruction 50
    else //general case2
    	result=Func(-a,-b); // instruction 70
    
    return result;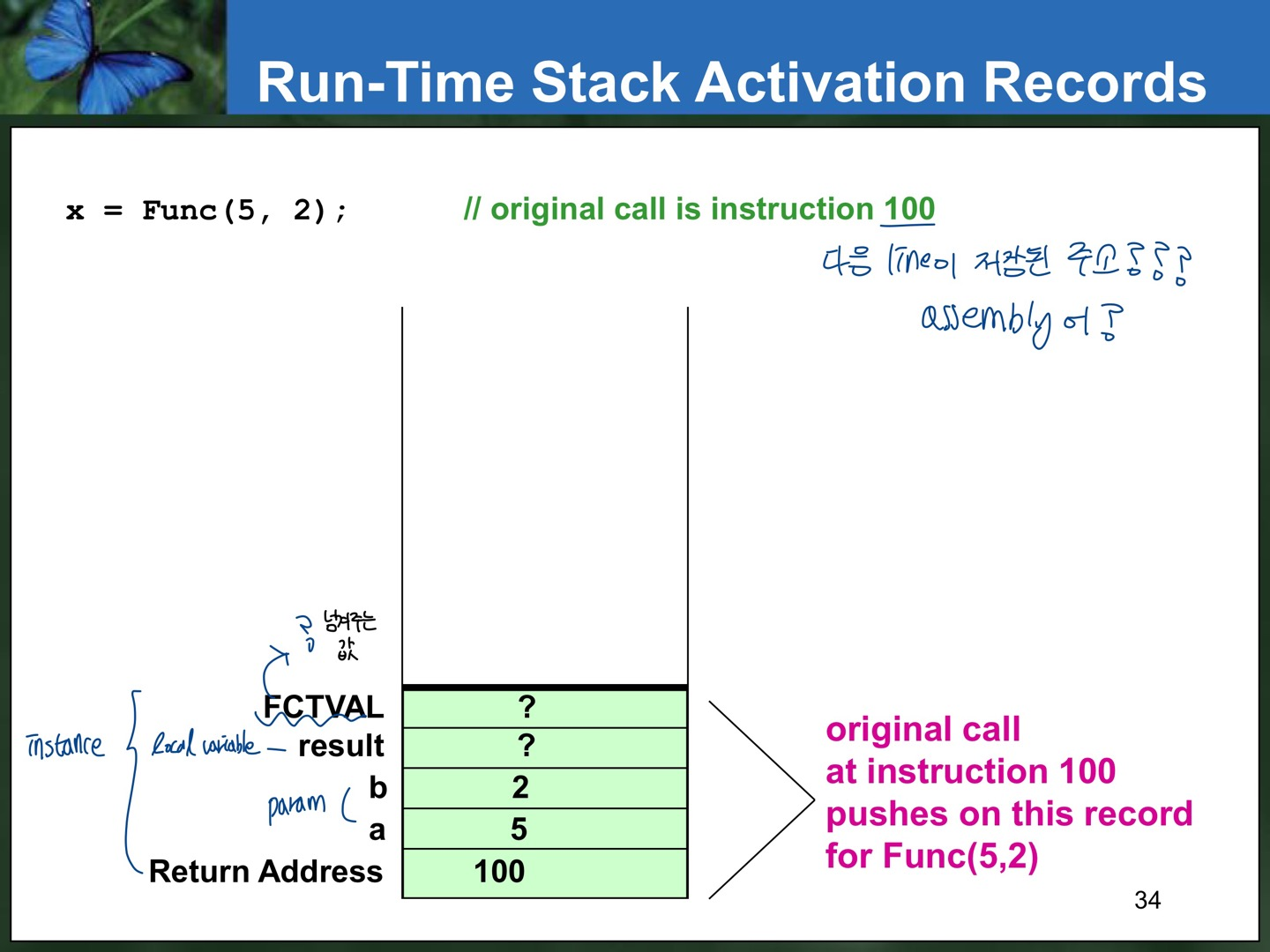

10. Sorted list의 InsertItem의 Recursive Implementation

size factor : 현재 리스트에 있는 원소의 수
base case
1 - 리스트가 비어있는 경우, 아이템을 빈 리스트에 넣는다.
2 - 맨 앞 아이템보다 작은 경우, 맨 앞에 넣는다.
general case : 다음 칸에서 재귀 호출을 한다.

template <class ItemType>
void Insert(NodeType<ItemType> *&location, ItmeType item)
{
	if( (location==NULL) || (item<location->info) // base case 
    // 비어있을 때 또는 맨 끝에 들어갈 때 OR 나보다 큰 값 찾았을 때 : STOP
    {
    	NodeType<ItemType<* tempPtr=location;
        location=new NodeType<ItemType>;
        location->info=item;
        location->next=tempPtr;
    }
    else
    	Insert(location->next, newItem); // general case
}

template <class ItemType>
void SortedType<ItemType>::InsertItem(ItemType newItem)
{
	Insert(listData, newItem);
}

여기서 가장 중요한 것은 reference 타입으로 받은 location의 포인터를 사용한다는 것이다.

* pointer : local variable 값을 주소로 갖는 일반 변수. 새 공간을 잡히고 location 변수에 영향을 주지 않는다.
*& : 파라미터가 location 공간과 동일한 공간을 의미하게 된다. 바뀌면 location도 바뀐다.

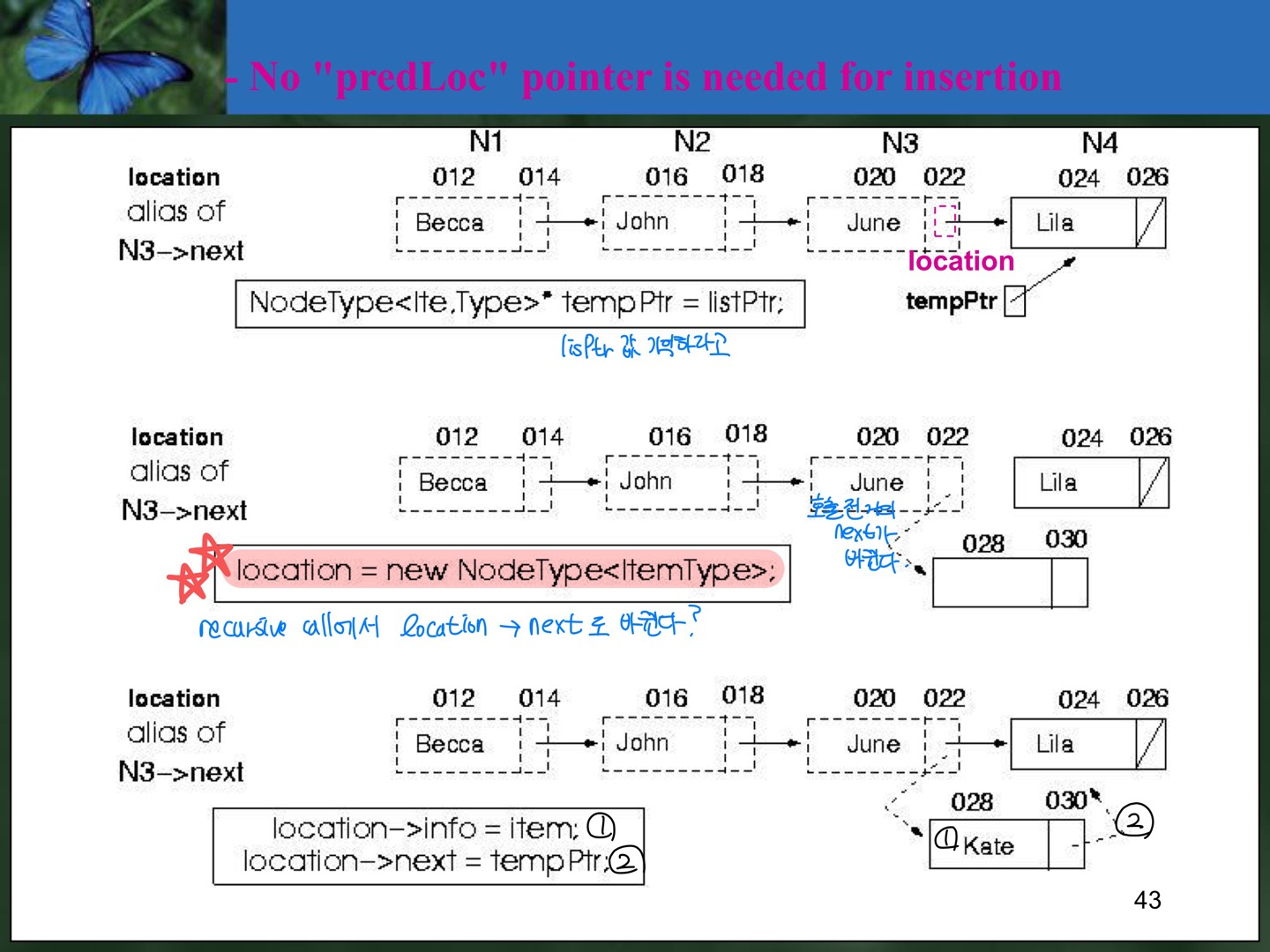
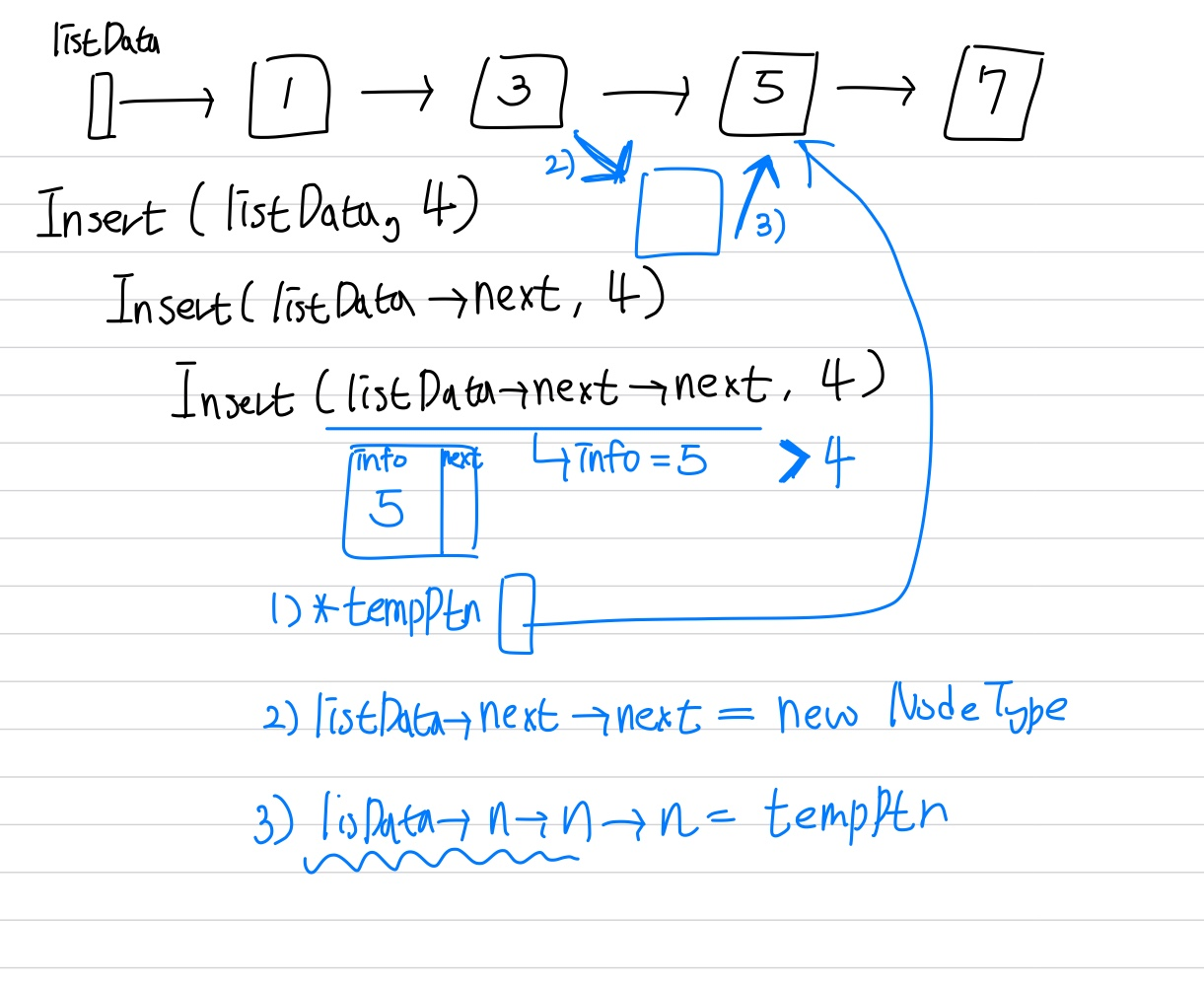
1) 현재 location 포인터가 가리키는 칸을 별도로 기억해둔다.
2) location 포인터가 새로 만든 칸을 가리키게 만든다. (location 자체가 새로운 값으로 바뀐다.)
3) 새로 만든 칸의 다음이 이전에 location이 가리키던 칸이 되도록 이어준다.
non-recursive인 loop로 만들기 위해선 앞의 노드의 값에 대한 정보인 predLoc 포인터를 두어서 값을 비교했는데, 이 predLoc이 필요가 없어진다. (선배님 velog에서 가져옴)

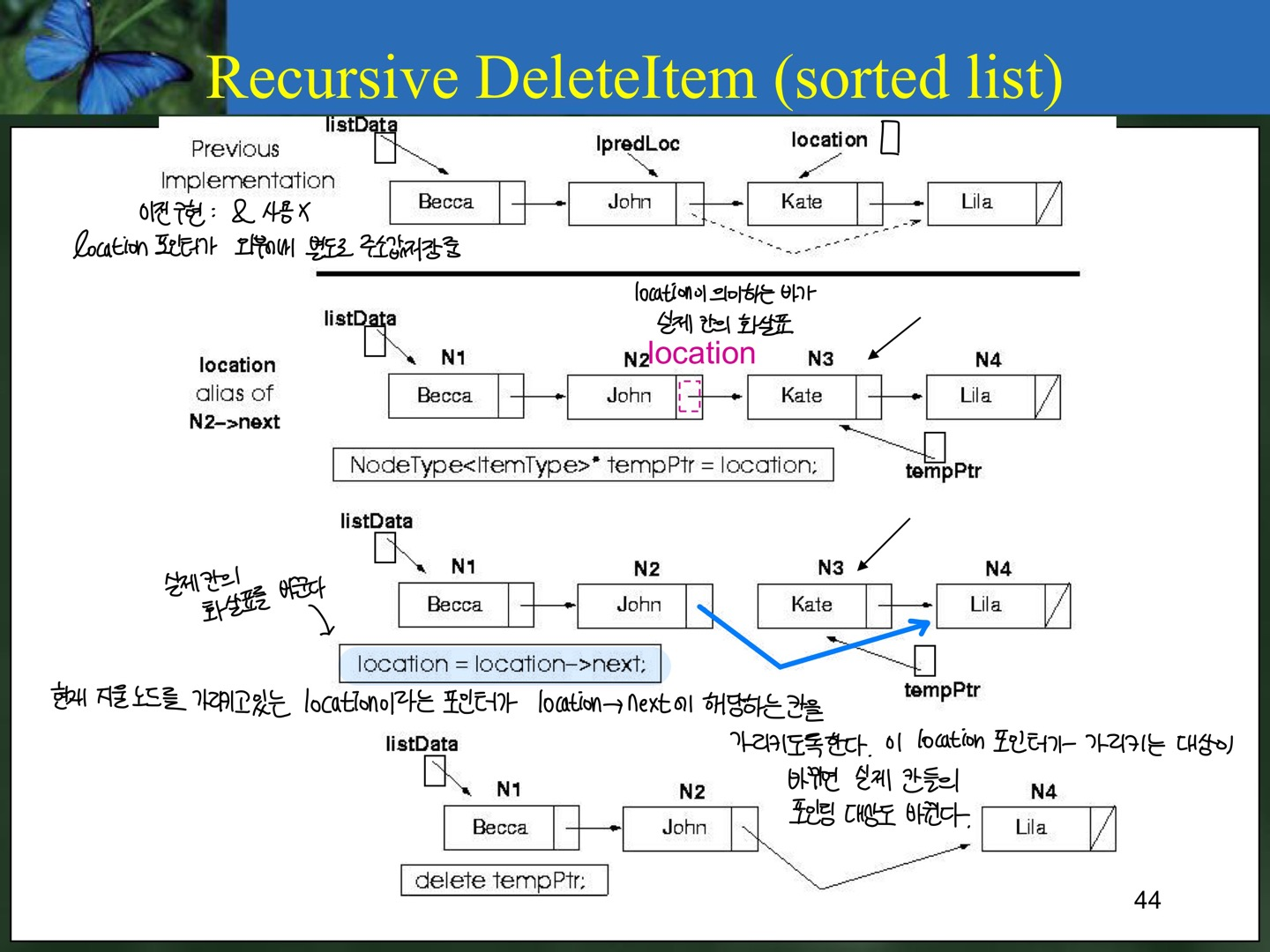
11. Sorted list의 DeleteItem의 Recursive Implementation

size factor : 리스트 원소 수
base case : location이 가리키는 칸의 info가 지울 아이템일 때 ( item == location->info) 지운다.
general case : 다음 칸에서 재귀 호출. Delete(location->next, item)

templace <class ItemType>
void Delete(NodeType<ItemType>* &location, ItemType item)
// 포인팅(화살표) 변경을 반영하도록 reference 타입으로 받는다. 앞의 next가 내 다음을 pointing 하도록 만든다.
{
	if (item==location->info)
    {
    	NodeType<ItemType>* tempPtr=location;
        location=location->next;
        delete tempPtr;
    }
    else
    	Delete(location->next, item);
 }
 
 template <class ItemType>
 void SortedType<ItemType>::DeleteItem(ItemType item)
 {
 	Delete(listData, item);
 }

12. Tail Recursion

함수의 가장 뒤에서 Recursion이 일어날 때를 Tail Recursion이라고 한다. Tail Recursion은 쉽게 Iteation 형태로 변경할 수가 있다. 함수의 파라미터와 지역 변수들을 저장할 필요가 없기 대문이다.
Tail이 아닌 경우 Loop로 변경하는 방법이 없을까. 저장해야 하는 정보들을 stack으로 집어넣었다가 나오면서 Pop을 한다면 가능할 것이다.

//Non recursive version - stacks : RevPrint()
// pre. stack을 구현한다.
void ListType::RevPrint()
{
	StackType<NodeType*> stack;
    NodeType* listPtr;
    listPtr=listData;
    
    while(listPtr!=NULL) // Put pointers onto the stack
    {
		stack.Push(listPtr);
        listPtr=listPtr->next;
    }
    
    while(!stack.IsEmpty()) // Retrieve pointers in reverse order and print elements
    {
		listPtr=stack.Top();
        stack.Pop();
        cout<<listPtr->info;
    }
 }

13. Recursion vs Iteration

branching structure
시간과 공간에 있어 덜 효율적이지만, 문제를 simplify하여 shorter source code가 되므로 쉽게 이해할 수 있다.
SHALLOW DEPTH, LOW EFFICIENCY, HIGH CLARITY

nothingisme

가볍게 재밌던 거 기록해요

다음 포스트