[자료구조] Chapter 8. Binary Search Trees

나도 자료구조가 좀 재밌으면 좋겠다. 이런 거 별로 재미없어 하는 거 보면 겜콘이 그립기도 하다. 나는 왜 자료구조나 알고리즘이 재미없을까. 기계학습은 그래도 재밌어 했는데. 나도 알다가도 모르겠다.

---

< Binary Tree의 특성 >
1. 각 노드는 최대 2개의 자식 노드를 가질 수 있다.

• 자신의 위에 있는 노드를 parent라 부른다.
• parent를 갖지 않는 노드인 시작 노드를 root라 부른다.
• 자식이 없는 노드를 leaf라 부른다.
• 따라서 list도 leaf 제외 모두 자식이 1개인 Binary Tree이다.

2. A unque path exists fom the root to every other node
   : 아래쪽(downward) 방향성 따라 내려가는 길을 path라고 부른다. parent node가 1개여야 한다는 것은 이 path가 unique하게 결정된다는 것을 의미한다.

< 트리와 관련된 용어 >

• 조상 노드(Ancestor of a node) : any node on path from the root to that node (parent, grandparent ...)
• 후손 노드(Descendant of a node) : any node on a path from the node to the last node in the path(child, grandchild ...)
• Level(depth) of a node : number of edges in the path from the root to that node
• Height of a tree : nubmers of levels

< Binary Tree의 종류 >

• Full Tree : a tree in which all of the leaves are on the same level and every nonleaf node has two child.
• Binary Tree가 L level이라고 할 때 Level당 최대 2^L 개의 노드를 가질 수 있다. 따라서 아래 사진은 등비수열의 합을 통해 트리가 가질 수 있는 최대 노드의 수를 구할 수 있다.
  
• 따라서 전체 노드의 수가 주어졌을 때 트리의 height를 계산할 수 있다.
• 만약 Linked List처럼 Level당 1개의 노드만 가지고 있다면, 높이가 최대가 된다.
• root 노드를 제외하고 모든 노드가 child 노드를 최대한 갖고 있다면 높이가 최소가 된다.
  
• 위에서 구한 공식은 2^h-1을 넣고 있다. 즉 Tree가 level 당 MAX Nodes라고 가정하고 있는 것이다. 따라서 Binary Tree라고 가정하고 전체 노드의 수가 주어지면 아래처럼 계산하면 된다.
  0개 : log 1 =0
  1개 : log 2 =1
  2개 : log 3 ~= 2, 3개 : log 4 = 2
  4~6개 : 최소 3
  7개 : log 8 = 최소 3
  8개~14개 : 최소 4
  15개 : 최소 4

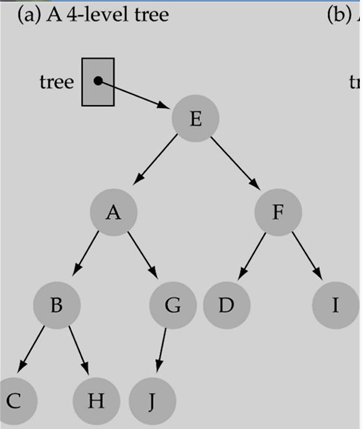
< Searching a binary tree >
1. start at the root
2. Search the tree level by level, until you find the element you are searching for
linked list처럼 생긴 경우 O(N)이 걸리므로 N개를 전부 살펴보는 것은 linked list와 마찬가지이다.

< BST에서 사용하는 Binary Tree의 특징 >
1. Each node contains a distinct data value : 중복 값 없다.
2. The key values in the tree can be compared using "greater than" and "less than" : 대소 비교가 가능하다. 크거나 작거나.
3. The key value of each node in the tree is less than every key value in its right subtree, and greater than every key value in its left subtree. : 모든 노드들이 오른쪽에는 자신보다 큰 값, 왼쪽에는 자신보다 작은 값들을 가진다.

< Binary Tree Search >
: 절반씩 버리면서 진행하므로 시간 복잡도는 O(logN)이 된다. linked list(: O(logN) )보다 낫다.

• 1) Start at the root
• 2) Compare the value of the item you are searching for with the value stored at the root
• 3) If the values are equal, then item found; otherwise, if it is a leaf node, then not found.
• 4) If it is less than the value stored at the root, then search the left subtree
• 5) If it is greater than the value stored at the root, then search the right subtree
• 6) Repeat step 2-6 for the root of the subtree chosen in the previous step 4 or 5

< BST Implementation >

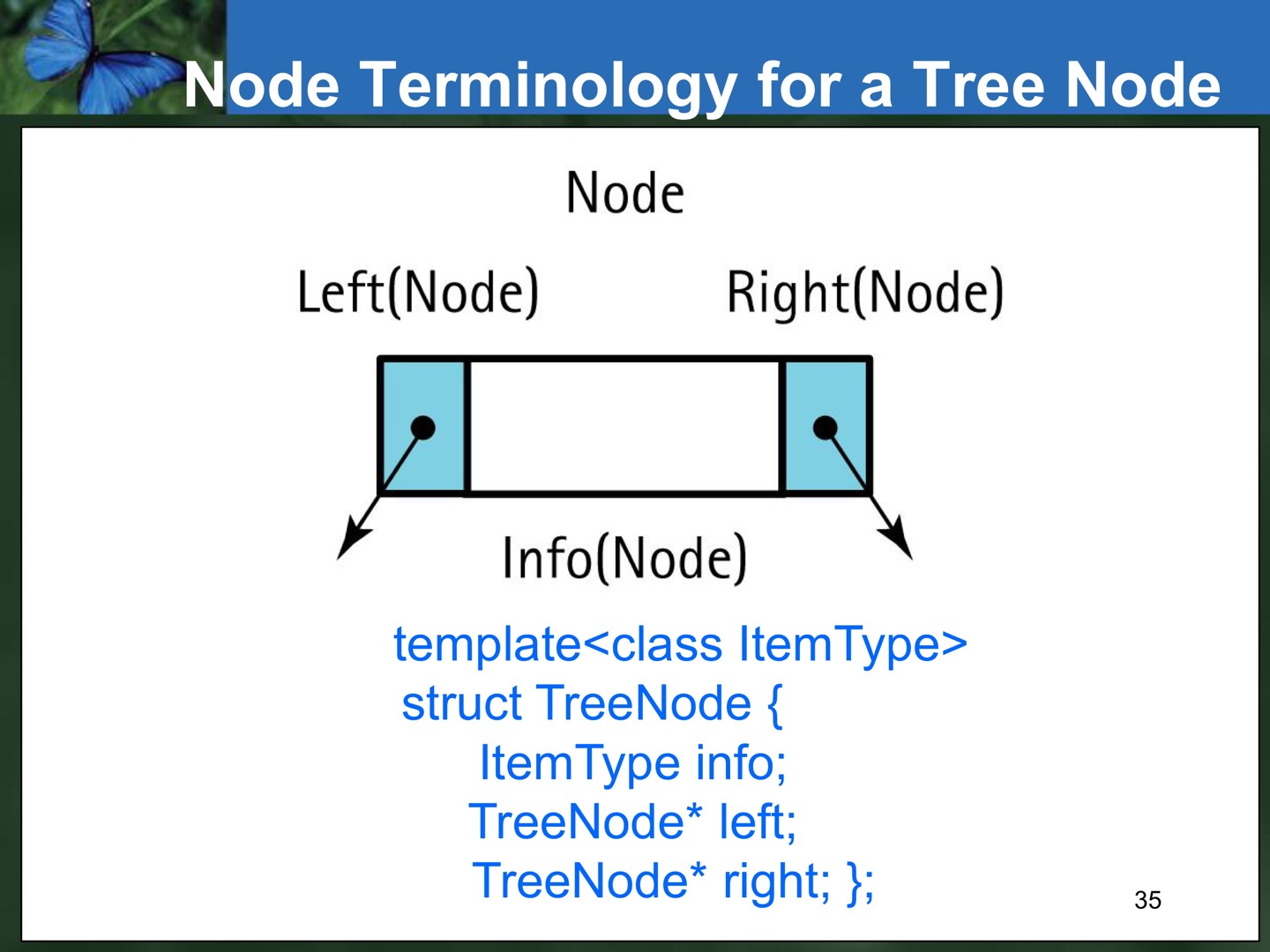
#include <fstream.h>

template<class ItemType>
struct TreeNode;

enum OrderType {PRE_ORDER, IN_ORDER, POST_ORDER};

template<class ItemType>
class TreeType {
	public:
    	TreeType(); // constructor
        ~TreeType(); // deconstructor
        TreeType(const TreeType<ItemType>&); // copy constructor
        void operator=(const TreeType<ItemType>&) // operator overloading
        void MakeEmpty();
        bool IsEmpty() const;
        bool IsFull() const;
        int LengthIs() const; // node 개수
        void RetrieveItem(ItemType&, bool& found); // copy 방지로 reference type으로 받는다.
        void InsertItem(ItemType);
        void DeleteItem(ItemType);
        void ResetTree(ItemType);
        void GetNextItem(ItemType&, OrderType, bool&); // enum에 정의. tree를 리스트 형태로 바꿔서 넣음
        // Next란게 존재하려면 순서대로 정렬되어있어야 하므로 list 형태로 바꿔야 한다.
        void PrintTree(ofstream&) const;
    private:
    	TreeNode<ItemType>* root;
 };

bool TreeType::IsFull() const
{
	NodeType* location;
    try
    {
		location=new NodeType;
        delete location;
        return false;
    }
    catch(std::bad_alloc exception)
    {
		return true;
    }
}

bool TreeType::IsEmpty() const
{
	return root==NULL;
}

• CountNodes 함수 구현 : Recursive Implementation
  { nodes in a tree } = { nodes in left subtree } + { nodes in right subtree } +1
  -size factor : number of nodes in the tree we are examining
  -base case : the tree is empty. NULL까지 갔을 때 -> return 0
  -general case : CountNodes( Left(tree) ) + CountNodes( Right(tree) ) +1

먼저 잘못 구현한 경우들을 살펴보자.

// 잘못 구현한 경우 1
if ((Left(tree) == NULL) && (Right(tree) == NULL)
	return 1;
else
	return CountNods(Left(tree))+CountNodes((Right(tree))+1;

이와 같이 구현하면 Left(tree)가 NULL일 때 문제가 발생한다. 즉 Left subtree는 NULL인데 Right Subtree는 NULL이 아닌 경우 base case가 없기 때문이다.

// 잘못 구현한 경우 2
if ((Left(tree) == NULL) && (Right(tree) == NULL) // 둘 다 NULL일 때
	return 1
else if (Left(tree) == NULL) // right은 NULL 아니고 left가 NULL일 때
	return CountNodes(Right(tree))+1;
else if (Right(tree) == NULL) // right는 NULL이고 left가 NULL 아닐 때
	return CountNOdes(Left(tree))+1;
else // general case
	return CountNods(Left(tree))+CountNodes((Right(tree))+1;

이와 같이 구현하면 initial tree가 NULL일 때 문제가 발생한다. 비어있는데 노드 개수를 1이라고 반환하는 것이다.

if (tree == NULL )
	return 0;
else if ( (Left(tree) == NULL ) && (Right(tree) == NULL)
	return 1;
else if (Left(tree) == NULL )
	return CountNodes(Right(tree))+1;
else if ( Right(tree) == NULL )
	return CountNodes(Left(tree))+1;
else
	return CountNods(Left(tree))+CountNodes((Right(tree))+1;

이를 간단하게 하면 다음과 같다. 재귀 호출 횟수는 1번 더 늘어나지만 코드가 simplify 된다.

if (tree == NULL )
	return 0;
else
	return CountNods(Left(tree))+CountNodes((Right(tree))+1;

이제 정말로 CountNodes 함수와 이를 통해 LengthIs 함수까지 해보자.

int CountNodes(TreeNode* tree);
int TreeType::LengthIs() const
{
	return CountNodes(root);
}

int CountNodes(TreeNode* tree)
{
	if (tree == NULL)
    	return 0;
    else
    	return CountNodes(tree->left) + CountNodes(tree->right)+1;
}

• RetrieveItem 함수 구현 => Recursive Implementation
  -size of factor : number of nodes in the tree we are examining
  -base cases : 1. when the key is found, 2. the tree is empty(key was not found)
  -general case : search in the left or right subtrees
  

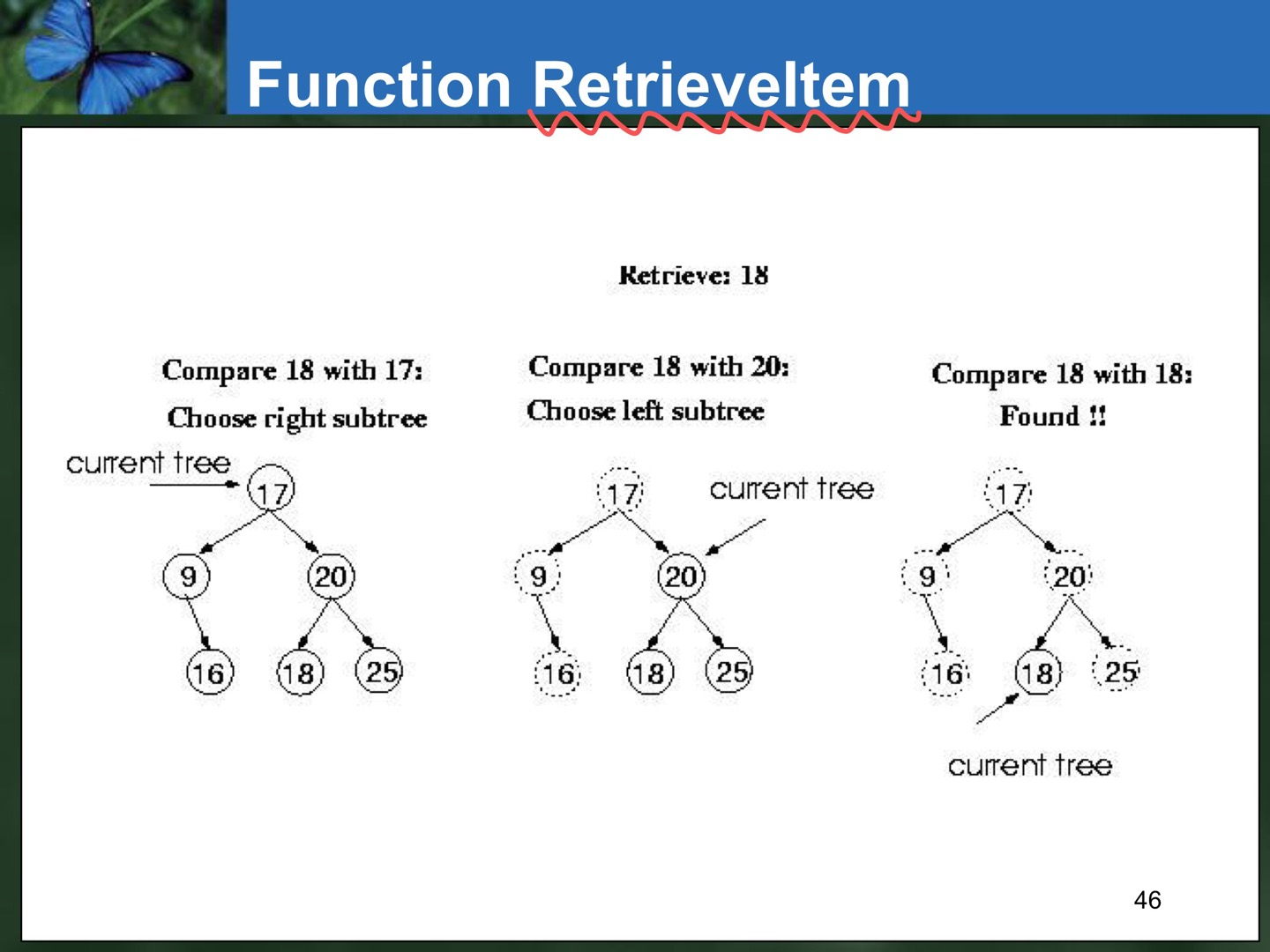
void TreeType::RetreiveItem(ItemType& item, bool& found)
{
	Retrieve(root, item, found);
}

void Retrieve(TreeNode* tree, ItemType& item, bool& found)
{
	if(tree==NULL) // base case 1 : 없을 때
    	found==false;
    else if (item<tree->info) // 찾고자 하는 값이 작으므로 왼쪽 subtree 살핀다.
    	Retrieve(tree->left, item, found);
    else if (item>tree->info) // 찾고자 하는 값이 크므로 오른쪽 subtree 살핀다.
		Retrieve(tree->right, item, found);
    else // base case 2 : 찾았을 때
    {
    	item=tree->info;
        found=true;
    }
}

• InsertItem Implementation
  : Reference Type으로 Parameter를 받고 Recursive Call을 하게 된다. 따라서 Insert된 Child 노드와 Parent 노드 사이에 Edge가 자동으로 알맞은 방향으로 생성된다.
  

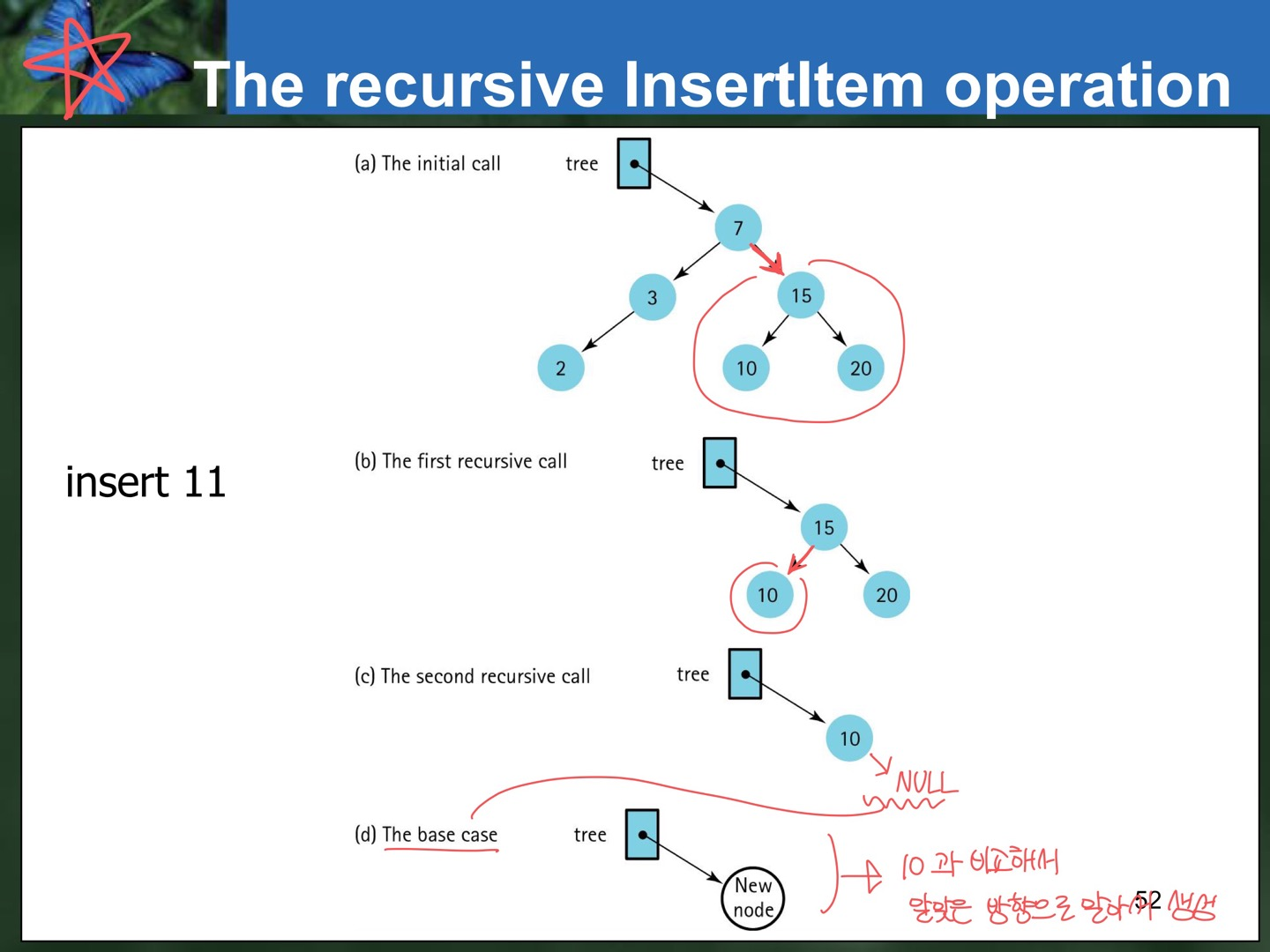
void Insert(TreeNOde*& tree, ItemType item) // ** reference type!! **
{
	if(tree==NULL)
    {
    	tree=new TreeNode; // **호출한 애의 tree->left/right가 바뀌게 된다. **
        tree->right=NULL;
        tree->left=NULL;
        tree->info=item;
    }
    else if(item<tree->info)
    	Insert(tree->left, item);
    else
    	Insert(tree->right, item);
}

• 트리에 값을 Inserting 할 때 순서가 중요할까?
  : 그렇다. A random mix of the elements prodives a shorter, bushy tree. Search가 간편해진다. Insert Order에 따라 unbalanced한 tree가 만들어질 수 있는데, 이러면 Search 시간이 증가한다.
  

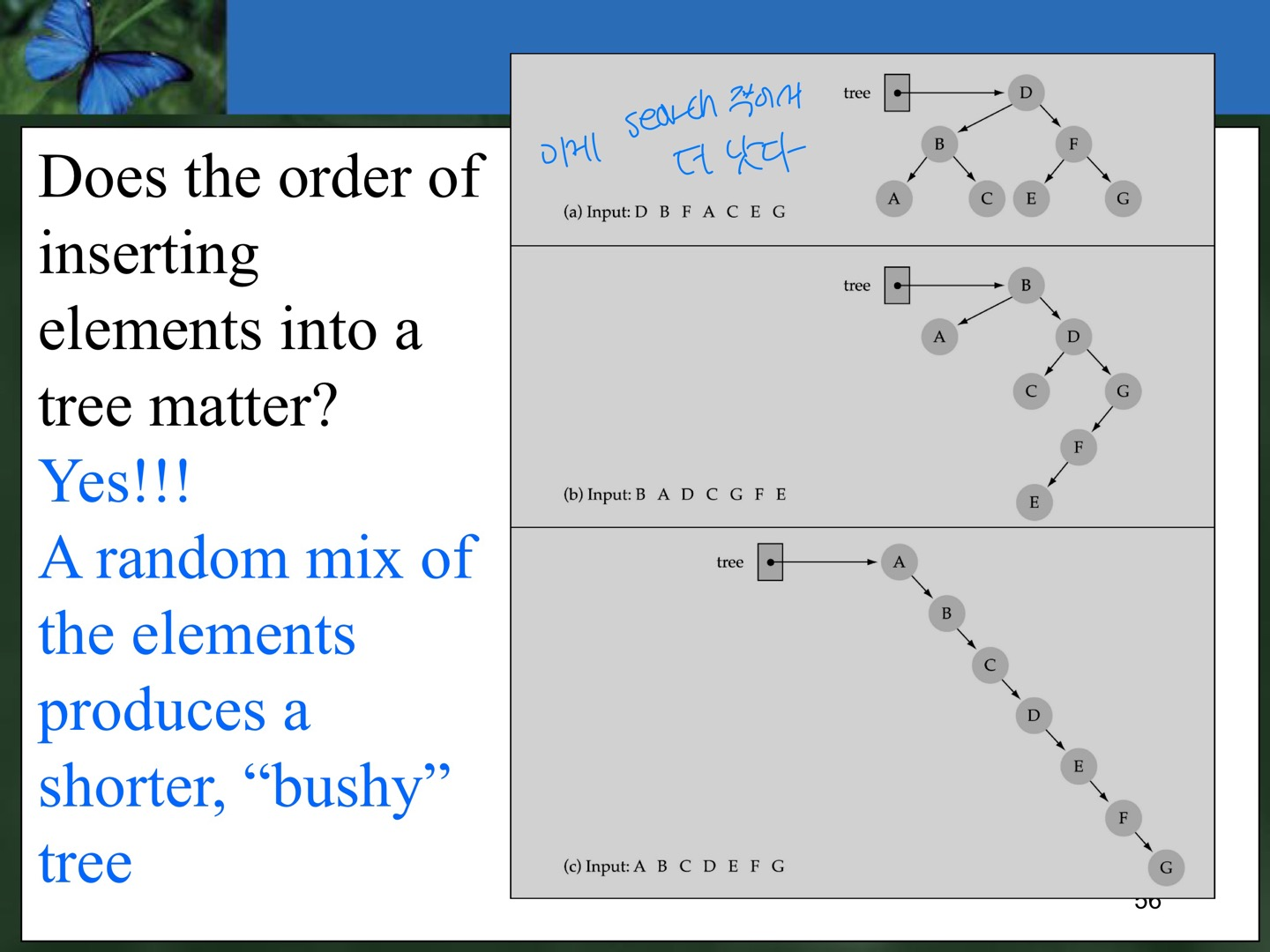
• DeleteItem Implementation
  지울 아이템을 찾고 지우는 과정을 수행한다. 그러나 이 경우 3가지로 case를 나눠야 한다.

1. Deleting a leaf (child가 0개인 경우)
2. Deleting a node with only one child
3. Deleting a node with two children
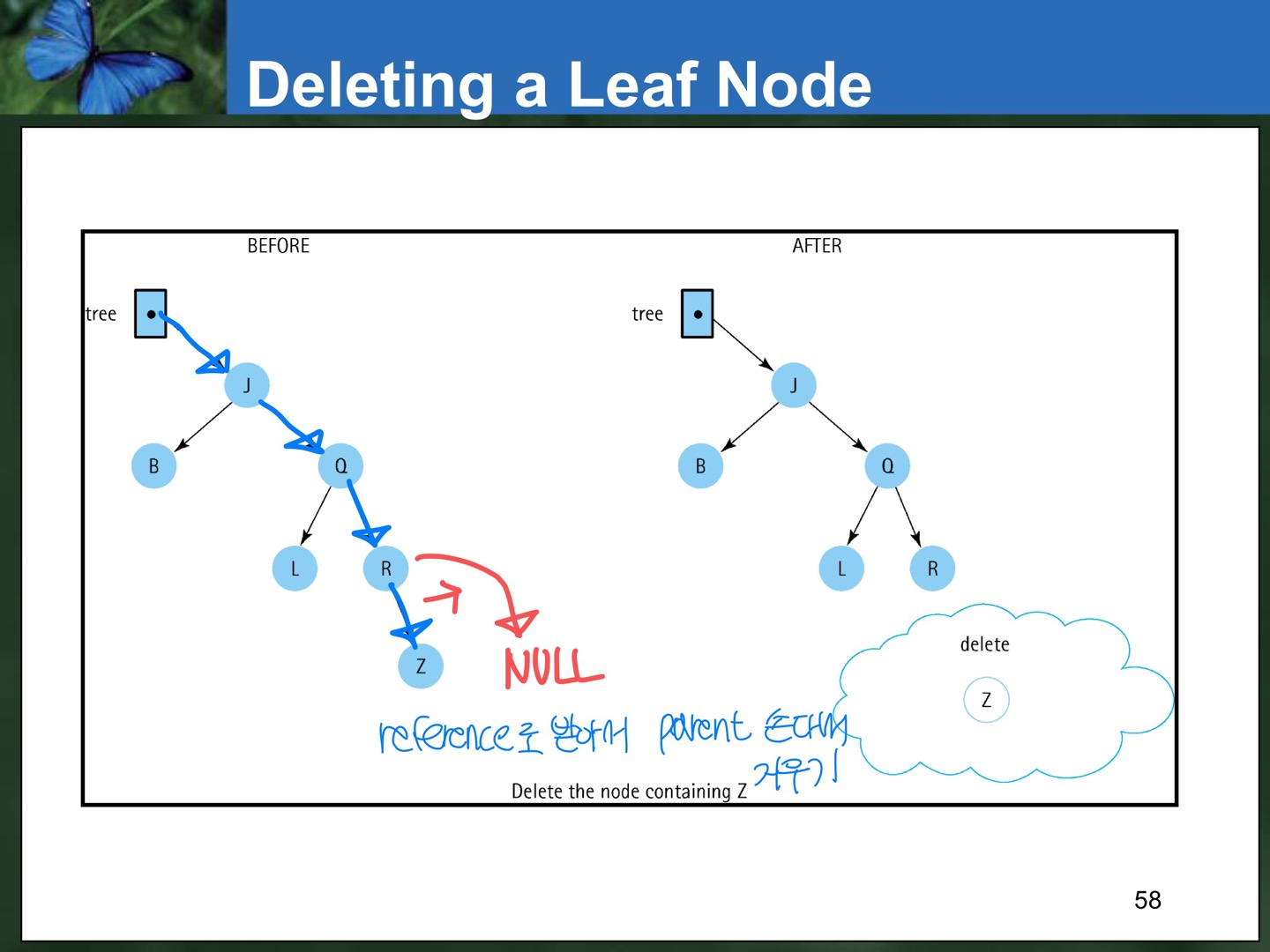   : child가 0개인 경우, 즉 leaf인 경우에는 parent를 reference로 건드려서 기존에 있던 위치에서 NULL을 가리키게 바꾼다.
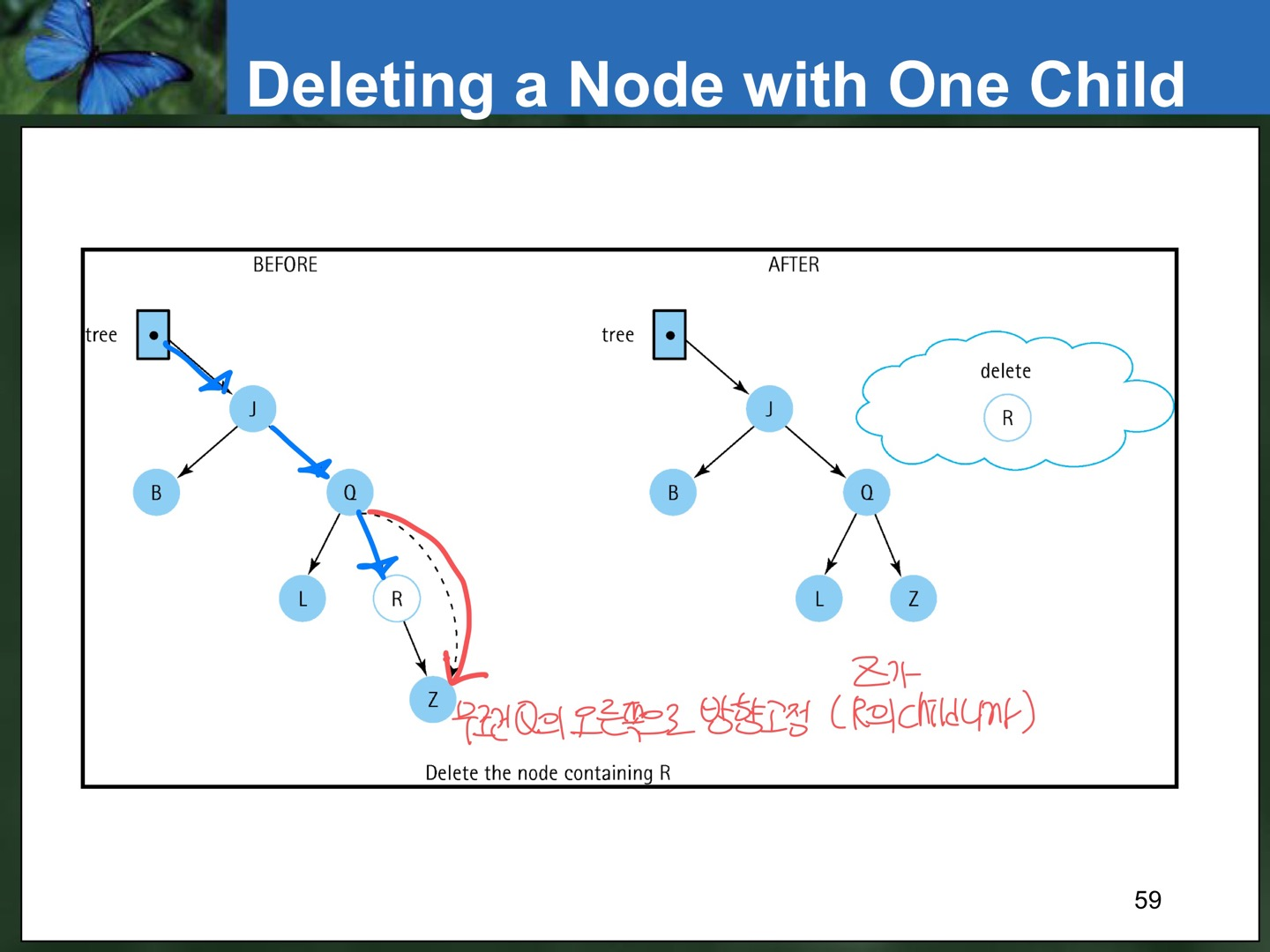   : child가 1개인 경우에 지우고자 하는 노드의 child와, 지우고자 하는 노드의 parent를 이어주면 된다. 즉, 자식이 부모의 자리를 대체하면 된다.
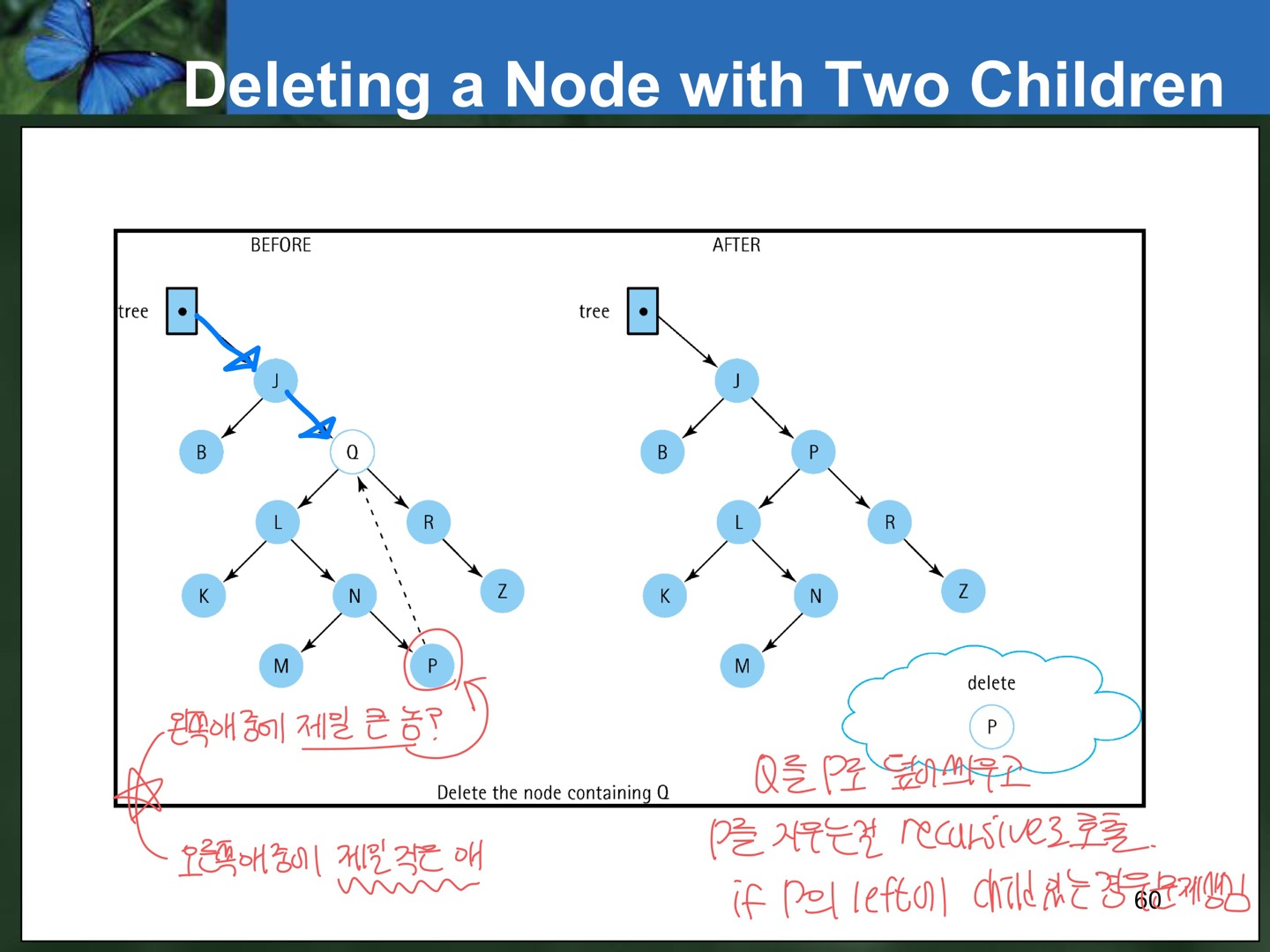   : child가 2개인 경우 해야하는 과정이 가장 복잡하다.
   1) Find predecessor (it is the rightmost node in the left subtree)
   2) Replace the data of the node to be deleted with predecessor's data
   3) Delete predecessor node

/*
if ((Left(tree) == NULL ) && ( Right(tree) == NULL )
	Set tree to NULL
else if ( Left(tree) == NULL)
	Set tree to Right(tree)
else if ( Right(tree) == NULL )
	Set tree to Left(tree)
else
	Find predecessor
    Set Info(free) to Info(predecessor)
    Delete predecessor
*/
void DeleteNode(TreeNode*& tree) // reference type!!!!!!!!!!!!!!!!!!
{
	ItemType data;
    TreeNode* tempPtr;
    tempPtr=tree;
    if(tree->left==NULL) 
    {
		tree=tree->right; // 0이면 tree->right이 NULL이기 때문
        delete tempPtr; // 0 or 1 children
    }
    else if (tree->right==NULL) 
    {
    	tree=tree->left;
        delete tempPtr; // 0 or 1 children
    }
    else  
    {
		GetPredecessor(tree->left, data);
        tree->info=data;
        Delete(tree->left, data); // // 2 children 재귀로 구현. 덮어씌운 애의 원래 위치 삭제.
    }
}

/*
Definition : Removes item from tree
Size : The number of nodes in the path from the root to the node to be deleted
Base case : If item's key matches key in Info(tree), delete node pointed to by tree
General case : If item < Info(tree), Delete(Left(tree), item);
				else Delete(Right(tree), item);
*/
void Delete(TreeNode*& tree, ItemType item)
{
	if(item<tree->info)
    	Delete(tree->left, item);
    else if(item>tree->info)
    	Delete(tree->right, item);
    else
    	DeleteNode(tree); // Node found
}

void GetPredecessor(TreeNode* tree, ItemType& data) // Recursive하게도 구현 가능
{
	while(tree->right!=NULL)
    	tree=tree->right;
    data=tree->info;
}

Q. 필기되어있는 것처럼 Delete node with 2 children에서 왼쪽 subtree의 가장 rightmost 노드가 left child를 가지고 있으면 어떡하지?