[프로그래머스] 아방가르드 타일링 - 파이썬/DP

https://school.programmers.co.kr/learn/courses/30/lessons/181186

import sys
sys.setrecursionlimit(10**6)
DP = [0]*100001

def solution(n):

    answer = block(n) % 1000000007

    return answer

def block(n):
    answer = 0

    if n==1:
        DP[1]=1
        return 1
    if n==2:
        DP[2]=3
        return 3
    if n==3:
        DP[3]=10
        return 10
    if n==4:
        DP[4]=23
        return 23
    if n==5:
        DP[5]=62
        return 62
    if n==6:
        DP[6]=170
        return 170

    if DP[n-1]:
        answer += DP[n-1]
    else:
        answer += block(n-1)
    if DP[n-2]:
        answer += DP[n-2]*2
    else:
        answer += block(n-2)*2
    if DP[n-3]:
        answer += DP[n-3]*6
    else:
        answer += block(n-3)*6
    if DP[n-4]:
        answer += DP[n-4]*1
    else:
        answer += block(n-4)*1
    if DP[n-6]:
        answer -= DP[n-6]*1
    else:
        answer -= block(n-6)*1

    DP[n]=answer

    return answer

이전에 백준에서 풀었던 문제와 결이 비슷하다고 생각했다. (https://www.acmicpc.net/problem/9095)

재귀와 DP를 활용하여 푸는 문제인데 다만 숫자가 아니고 도형이다.

예를 들어서 숫자로 3을 만든다고 치면

1+1+1, 1+2, 2+1, 3 으로 만들 수 있는데 이것을 도형에 접목시켜보면

이 모형이 1이다.

1을 두개 붙인 것도 2이지만

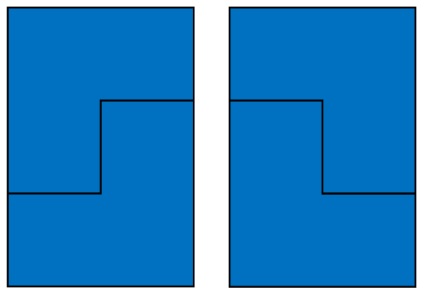
이 파란색 모형 두개를 붙인 것은 1+1로 표현이 불가능한 고유의 2라고 생각했다.

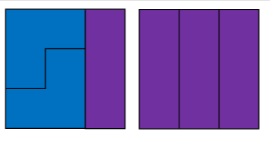
같은 3을 표현할지라도 앞의 그림은 2+1, 뒤의 그림은 1+1+1로 생각할 수 있다.

그런데 2를 만드는 방식도 2가지가 있고, 3 역시 아래처럼 5개의 고유의 모형을 가진다.

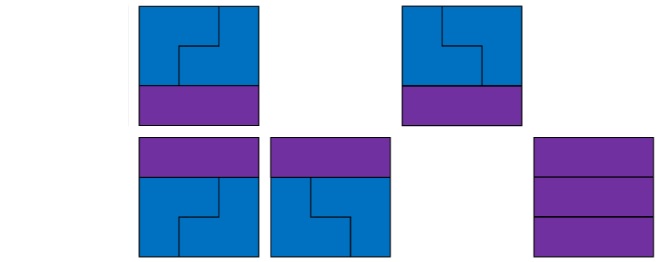
즉, 3을 나타내는 방법을 계산해보면

1+1+1+1 => 1개
1+2 => 1개 * 2 (2를 표현하는 방법이 2가지)
2+1 => 1개 * 2 (2를 표현하는 방법이 2가지)
3 => 5개 (3을 표현하는 고유의 방법)

1+2+2+5 = 10

10이 나오는 것이다.

마찬가지로 4,5,6도 같은 방법으로 표현할 수 있는데 4,5,6도 아래와 같은 2,2,4개의 고유의 모형을 가지고 있다.

7,8,9는 각각 4,5,6의 고유모형 내부를 3칸씩 늘린 것과 똑같다.

즉, n=10일때 식을 세워보면 아래와 같다.

DP(10) = DP(9) + 2*DP(8) + 5*DP(7)
+ 2*DP(6) + 2*DP(5) + 4*DP(4)
+ 2*DP(3) + 2*DP(2) + 4*DP(1)
+ 2

그런데, DP(n)을 구하는데 DP(n-4)부터는 반복되는 구간이 나타나므로 DP(n+3)에서 DP(n)을 빼서 하위 구간을 삭제할 수 있다.

DP(13) - DP(10) = DP(12) + 2*DP(11) + 5*DP(10)
+ DP(9) - DP(7)

이 식을 바꿔보면

DP(13) = DP(12) + 2*DP(11) + 6*DP(10) + DP(9) - DP(7)

즉, 아래와 같은 점화식을 세울 수 있다.

DP(x) = DP(x-1) + 2*DP(x-2) + 6*DP(x-3) + DP(x-4) - DP(x-6)

위에서 세운 점화식을 토대로 재귀를 하면 정답을 구할 수 있다.