이진 탐색(Binary Search)

개요

먼저 이진 탐색(Binary Search)의 정의부터 살펴보겠습니다. 이진 탐색이란 오름차순으로 정렬된 리스트의 값에서 특정한 값의 위치를 찾는 것이다. 처음 중간의 값을 임의로 선택하며 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 사용한다.

이진탐색은 리스트에만 사용이 가능하다는 단점이 있지만, 검색을 할 때마다 탐색 데이터의 수가 직전 데이터의 절반이 되므로 속도가 빠르다는 장점이 있습니다.

말로만 설명하면 이해가 잘 되지 않으실 겁니다. 이진탐색은 다음 그림과 같이 탐색이 진행됩니다.

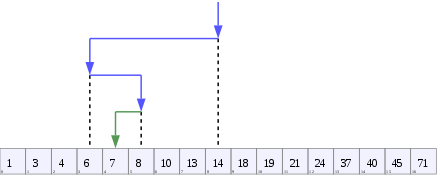
그림 출처 :https://en.wikipedia.org/wiki/Binary_search_algorithm

동작방식

위 그림을 예시로 동작 방식을 설명하겠습니다. 시작 조건은 리스트에는 17개의 요소가 있으며 찾고자 하는 값은 7입니다. 처음에는 중앙값을 찾습니다 중앙값은 리스트의 17개의 요소중 중간에 있는 값(n개의 요소면 n / 2)이며 8번째의 값(14)이 중앙값이 됩니다. 그다음은 이 중앙값과 (14) 찾고자 하는 값 (7)을 비교를 합니다, 여기서 찾고자 하는 값의 값이 중앙값보다 작으므로 큰 오른쪽에 있는 숫자들은 제외를 합니다.(18, 19, 21, 24, 37, 40, 45, 71)

이번엔 [1, 3, 4, 6, 7, 8, 10, 13, 14]의 리스트에서 위와 같은 방식으로 진행을 합니다. 중앙값의 위치는 4, 중앙값은 6이 됩니다. 그리고 역시 중앙값(6)과 찾고자 하는 값 (7)을 비교하고 여기선 찾고자 하는 값이 중앙값보다 더 크므로 중앙값보다 작은 값[1, 3, 4]들을 제외시켜줍니다.

이번엔 [6, 7, 8, 10, 13, 14]의 리스트에서 위와 같은 방식으로 진행을 합니다. 중앙값의 위치는 3, 중앙값은 8이 됩니다. 그리고 역시 중앙값(8)과 찾고자 하는 값 (7)을 비교하고 여기선 찾고자 하는 값이 중앙값보다 작기 때문에 8보다 큰 오른쪽의 값[10, 13, 14]을 제외시켜줍니다.

이번엔 [6, 7, 8]의 리스트에서 위와 같은 방식으로 진행을 합니다. 중앙값의 위치는 2, 중앙값은 7이 됩니다. 그리고 역시 중앙값(7)과 찾고자 하는 값 (7)을 비교하고 여기서 중앙값과 찾고자 하는 값이 같기 때문에 최종적으로 이 리스트의 위치를 반환해줍니다.

시간 복잡도

처음의 이진탐색의 리스트를 N으로 가정하고 진행하겠습니다. 어떤 값을 찾고자 하여 이진 탐색을 사용하면 리스트에서 N의 값이 제외되기 때문에 N / 2이 됩니다. 그리고 값을 찾지 못하였다면 또 직전의 값에서 (N / 2) / 2 가 되고 이렇게 계속 리스트의 절반이 제외가 됩니다. 여기에서 규칙은 매 시행 때마다 탐색할 데이터의 양이 반으로 줄어들고 있기 때문에 N개의 자료에서의 시행 횟수는 Big O 표기법으로 O(logN)으로 나타낼 수 있습니다.

구현

이진탐색(Binary Search)의 구현은 아래의 코드를 참조해 보시면 될 것 같습니다.
주의할 점은 매개변수의 리스트는 정렬된 리스트입니다.

public static int binarySearch(int[]list, inttarget) {
    int left = 0, right =list.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;

        if (list[mid] ==target) {
            return mid;
        }else if (list[mid] >target) {
            right = mid - 1;
        }else if(list[mid] <target) {
            left = mid + 1;
        }
    }
    return -1;
}