힙(heap) 이란?
- 영단어로써의 힙(heap)은 ‘무엇인가를 차곡차곡 쌓은 더미’라는 뜻을 가지고 있다.
- 힙은 항상 완전 이진 트리의 형태를 가지고 있다.
- 힙에서는 가장 높은 또는 가장 낮은 우선순위를 가지는 노드가 항상 뿌리(root) 노드에 오기 때문에, 최댓값과, 최솟값을 O(1)안에 찾을 수 있다.
- 힙 트리에서는 중복된 값을 허용한다. (완전 이진트리는 불가능)
힙(heap)의 삽입과 삭제
루트 노트(root node)는 항상 우선순위가 가장 높은 노드이다, 이러한 원리가 있어서 최대값과 최소값을 빠르게 찾을수 있으며 (시간 복잡도: O(1)) 삽입과 삭제시에도 부모와 자식노드간의 부모의 우선순위가 자식의 노드보다 높으면 되기때문에 (시간 복잡도: O(logN))의 빠르게 데이터를 삽입과 삭제를 할 수 있다.
삽입
-
힙에 새로운 요소가 들어오면 마지막 노드에 힙을 추가한다.
-
새로운 노드를 부모노드와 비교를 하여 힙의 성질을 만족시킨다.
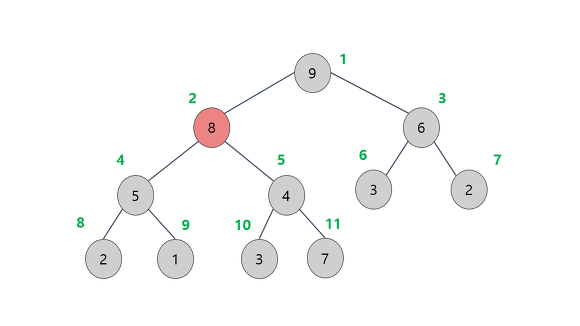
삭제
- 힙의 최대 힙(루트 노드)를 삭제한다.
힙의 종류가 최대 힙(Max-heap)이기 때문에 루트 노드가 최대값이다. - 삭제 된 루트노드에는 가장 마지막의 노드를 가져온다.
- 삽입 된 노드와 자식 노드를 비교하면서 힙의 성질을 만족시킨다.
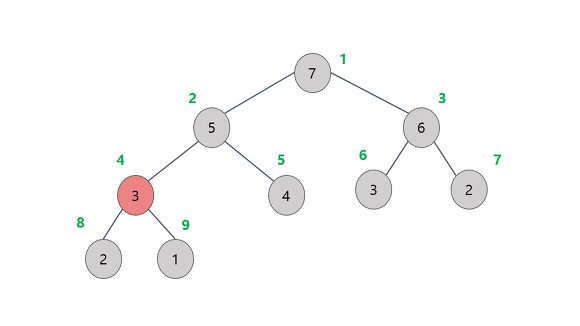
힙(heap)의 종류
일반적으로 힙은 두 가지의 타입을 가진다.
키 값의 대소관계는 항상 부모노드와 자식노드간의 관계에서만 성립하며, 형제 사이에는 대소관계가 성립 하지 않는다.
- 최대 힙 (Max-Heap) : 부모 노드의 키 값이 자식노드의 키 값보다 항상 큰 힙
- 최소 힙 (Min-Heap) : 부모 노드의 키 값이 자식노드의 키 값보다 항상 작은 힙 .png)
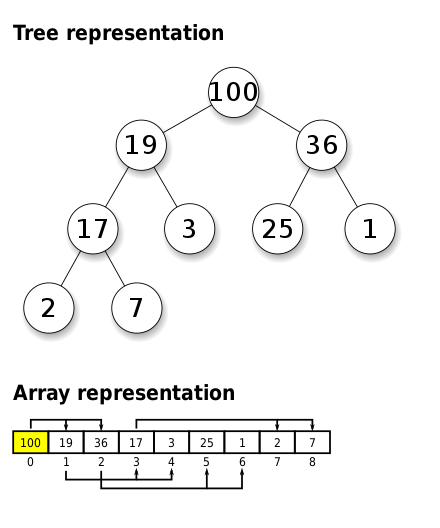
힙(heap) 구현
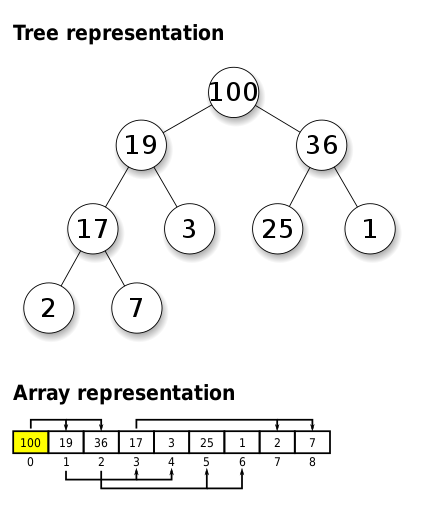
- 힙의 구현은 배열과 연결리스트로 구현할 수 있다.
- 표준적인 방법으로는 ‘배열’을 많이 사용한다.
- 이 글에서는 배열과 최소힙으로 구현하여 보겠다.
- 힙에서 부모노드와 자식노드의 관계
- 부모노드 인덱스(3) = 왼쪽 자식노드 / 2 (6)
- 왼쪽 자식노드 인덱스(6) = 부모노드 * 2
- 오른쪽 자식노드 인덱스 (7) = 부모노드 2 + 1 (3 2 + 1)
구현 과정
위에서 봐왔듯이 힙(heap)은 부모 노드의 인덱스를 알면 자식 노드의 인덱스를 알 수가 있다. 이러한 특징을 사용하여 heap을 구현해 보겠다.
- 삽입할 원소를 heap의 마지막 인덱스에 추가시킨다.
- 마지막 인덱스에서 나누기 2를하여 부모 노드의 인덱스를 찾는다.
- 부모의 값과 비교한다.
- 위의 과정을 반복한다. (종료조건: 루트 노드가 되거나, 부모의 노드가 현재 노드보다 작을 때)
힙 정의
class Minheap {
private ArrayList<Integer> heap;
public Minheap() {
heap = new ArrayList<>();
heap.add(0);
}데이터 삽입
//힙 삽입
private void insert(int val) {
heap.add(val);
int pos = heap.size() - 1;
//루트 노드에 도달하거나, 부모노드가 자식노드보다 작아질 때 까지 반복
while (pos > 1 && heap.get(pos / 2) < heap.get(pos)) {
//swap
int tmp = heap.get(pos / 2);
heap.set(pos / 2, heap.get(pos));
heap.set(pos, tmp);
pos /= 2;
}
}
데이터 삭제
private int delete() {
if (heap.size() < 1) {
return 0;
}
int deleteData = heap.get(1); //루트 노드 삭제
//가장 아래에 있는 노드 루트 노드로
heap.set(1, heap.size() - 1);
//옮겨진 노드 삭제
heap.remove(heap.size() - 1);
int pos = 1;
while ((pos * 2) < heap.size()) {
int min = heap.get(pos * 2); //값
int minPos = pos * 2; //왼쪽 자식 인덱스
//왼쪽 자식과 오른쪽 자식값 비교
if ((pos * 2 + 1) < heap.size() && heap.get(pos * 2 + 1) > min) {
//오른쪽 값이 더크면 왼쪽이랑 바꿔준다.
min = heap.get(pos * 2 + 1);
minPos = pos * 2 + 1;
}
if (heap.get(pos) < min) break;
//swap
int tmp = heap.get(pos);
heap.set(pos, heap.get(minPos));
heap.set(minPos, tmp);
pos = minPos;
}
return deleteData;
}
}
