Affine Space

Point vs Vector

점과 벡터는 표현되는 방식이 비슷하지만 ($v=(1,1,0)$, $p=(1,1,0)$) 다른 개념이다.

점은 고정되어 있지만 벡터는 방향과 크기만을 가지고 있을 뿐 좌표와는 무관하다.

벡터는 상대적인 개념이기 때문에 두 점의 변위라고 생각할 수 있다.

즉 하나의 벡터가 주어졌다고 해서 좌표 어딘가에 고정되지 않고

좌표에 상관없이 그러한 방향과 크기를 가지고 있는 모든 곳에서 존재할 수 있다.

이러한 개념은 Coordinate-Free라고 한다.

비유하자면 점은 시각, 벡터는 시간이라고 생각할 수 있다.

Homogeneous Coordinate

동차좌표(Homogeneous Coordinate)를 사용하면 점과 벡터의 차이가 더 명확하게 보인다.

점 $p=(1,1,2)$, 벡터 $v=(2,2,3)$에 대하여 동차좌표로 나타내면

점은 뒤에 1을 추가해 $p_1=(1,1,2,1)$,

벡터는 뒤에 0을 추가해 $v_1=(2,2,3,0)$로 나타낼 수 있다.

합연산

두 점에 대하여 합연산을 할 수 있을까?

$p_1 + p_1=(1,1,2,1)+(1,1,2,1) = (2,2,4,2)$

점은 좌표에서 한 지점을 나타내는 개념이기 때문에 +라는 개념이 무의미하다.

위와 같이 계산 결과를 보면 맨 뒤의 수가 2가 되기 때문에 점이 아닌 무언가가 되어버린다.

반면, 벡터는 합연산이 가능할까?

$v_1+v_1=(2,2,3,0)+(2,2,3,0)=(4,4,6,0)$

벡터는 변위(변화한 위치)라는 개념이라는 개념이기 때문에 +라는 개념이 자연스럽다.

위와 같이 계산 결과도 맨 뒤의 수가 0으로 유지되어 벡터가 유지되는 모습이다.

Subtraction

$p_1 - p_2=(3,2,3,1)-(1,1,2,1) = (2,1,1,0)$

두 점의 변위가 벡터의 정의이다. 위 계산처럼 점과 점의 뺄셈은 벡터가 되는 모습이다.

벡터끼리의 계산도 해본다면 여전히 벡터가 됨을 알 수 있다.

Scalar Multipulication

scalar * vector = vector

1 * point = point

0 * point = vector

c * point = undefined

그래서 Affine Space은?

vector space을 확장해 점과 그 관련된 연산들을 포함한 공간이다.

원점 O 와 공간을 이루는 기저 벡터들로 이루어져 있다.

$p= O +c_1v_1+c_2v_2+c_3v_3...$

$v= c_1v_1+c_2v_2+c_3v_3...$

모든 점과 벡터는 위와 같이 표현된다.

Coordinate System & Reference Frame

둘이 혼용해서 사용해도 문제는 없지만 엄밀히 따지자면

coordinate system은 물체의 위치를 나타내기 위해 사용하고

reference frame은 물체의 움직임을 나타내기 위해 사용한다.

World / Body Frame (Coordinate System)

world frame

우리가 구성하려는 세계의 프레임이다. 모든 물체의 위치는 상대적이기에 하나의 기준을 정한다고 생각하면 된다.

건물 안의 책상을 표현하기 위해 건물을 world frame으로 설정할 수 있다.

body frame

우리가 나타내려는 물체의 프레임이다. world frame에서의 물체 위치를 바로 구할 수도 있지만

조금 까다로운 작업이기에 물체의 프레임을 따로 설정하고

world frame에 대한 body frame의 변환 정도를 계산해

물체의 모든 점을 변환하는게 훨씬 편하다.

Affine Transformation Matrix

Affine Space에서의 변환을 알아보자

World Frame에서의 물체 이동

물체를 이루는 모든 점에 대해 똑같은 변환 M을 적용한다면 물체가 이동되는 것과 같다.

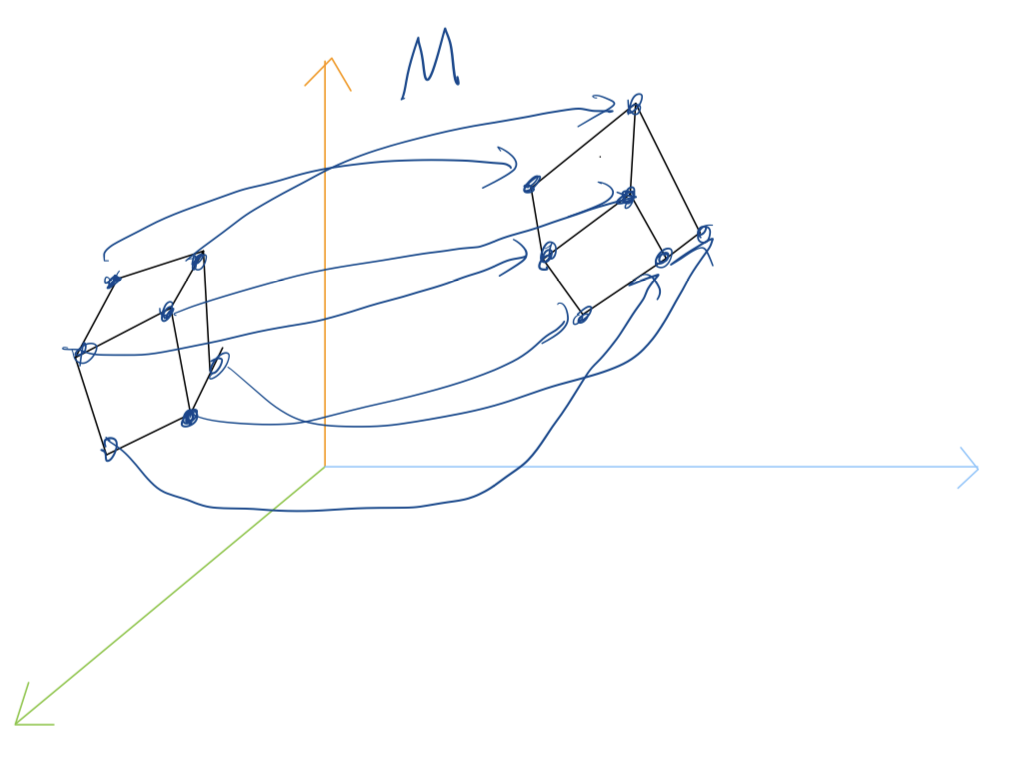
frame 이동

하나의 frame을 이루는 원점과 벡터들을 모두 이동시키는 것이다.

예를 들어 기본 world frame

$O=(0,0,0,1)$

$v_1=(1,0,0,0), v_2=(0,1,0,0), v_3=(0,0,1,0)$

을 변환 $M= \begin{bmatrix} m_1&m_2&m_3&s_1\\ m_4&m_5&m_6&s_2\\ m_7&m_8&m_9&s_3\\ 0&0&0&s_4 \end{bmatrix}$ 시켜보자

각각 모두 곱해주면

$O'=M*O=(s_1,s_2,s_3,1)$
$v_1'=M*v_1=(m_1,m_4,m_7,0)$
$v_2'=M*v_2=(m_2,m_5,m_8,0)$
$v_3'=M*v_3=(m_3,m_6,m_9,0)$

이 네가지로 이루어진 Affine Frame이 새로운 프레임이다.