Affine Transformation

Afffine Transformation

Affine Transformation은 변환들 중에서 우리에게 가장 친숙한 변환이다.

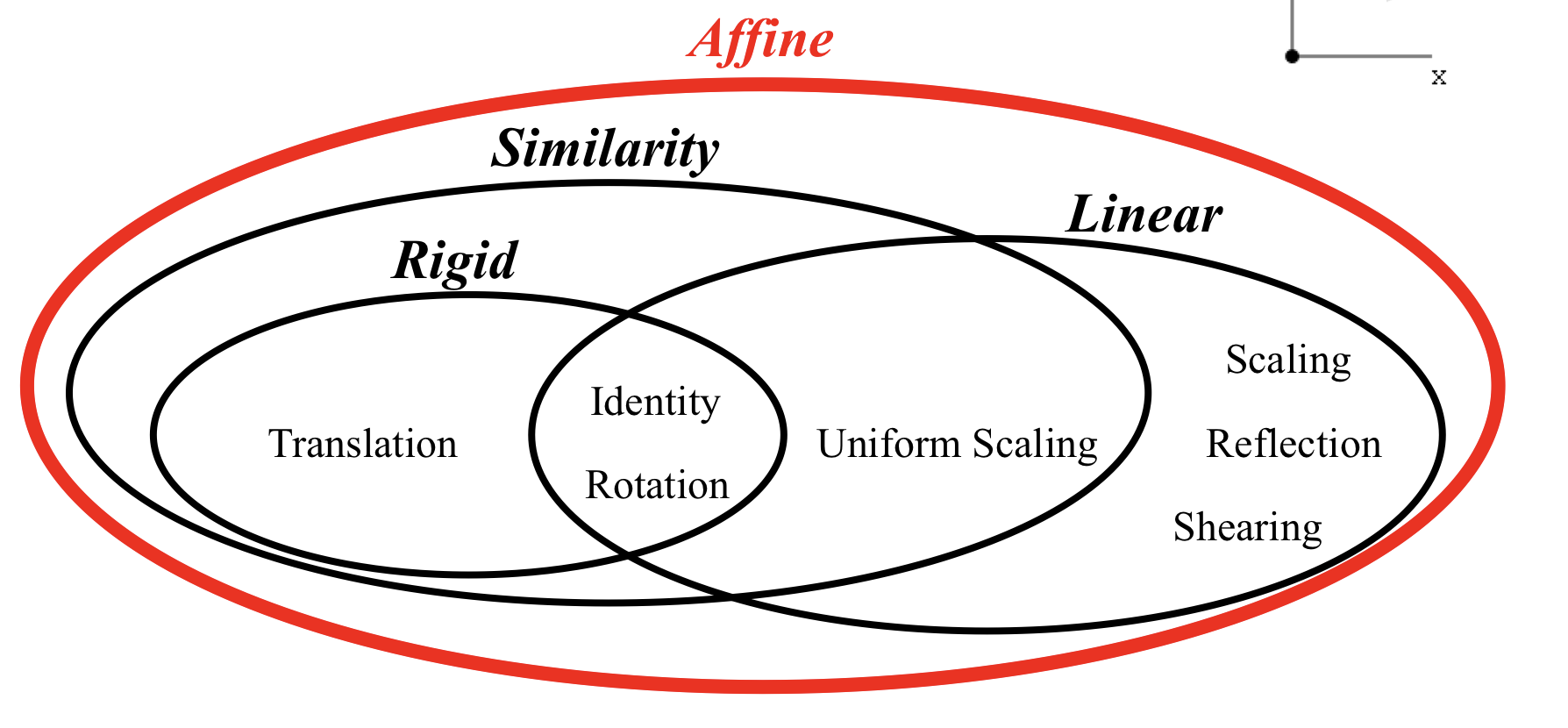
각 변환들은 다음과 같은 성질을 가지고 있다.

• Rigid : 변환하였을 때 점들 사이의 길이, 각도가 유지된다.
• Similarity : 점들 사이의 각도가 유지된다.
• Linear : 원점은 변환이 일어난 후에도 원점이다.
• Affine Transformation : 평행선들이 유지되고 점 간격의 비율이 유지된다.

cf. Reflection은 similarity로 분류하는 사람도 있다.

Linear Transformation이란

행렬의 곱으로 변환을 나타낼 수 있다면 linear transformation이라 부른다.

즉 변환시키고 싶은 점을 v라고 한다면

$T(v) = M*v$ 꼴로 나타낼 수 있는 모든 $T(v)$이다.

Linear Transformation 종류

처음에 이런 모양으로 시작한다 했을때

uniform scaling

(기저 벡터의) 모든 방향으로 일정하게 확대/축소

$M=\begin{bmatrix}2&0\\0&2\\ \end{bmatrix}$

non-uniform scaling

특정 방향으로만 확대/축소

$M=\begin{bmatrix}2&0\\0&1\\ \end{bmatrix}$

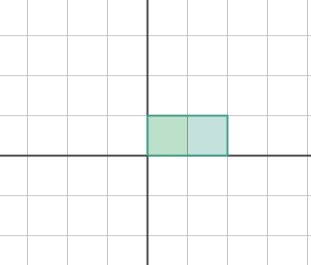
rotation

원점 중심 회전 (반시계 방향이 +$\theta$방향)
$M=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\\ \end{bmatrix}$

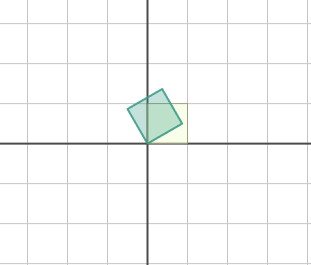
shearing

기울이기
$M=\begin{bmatrix}1&2\\0&1\\ \end{bmatrix}$

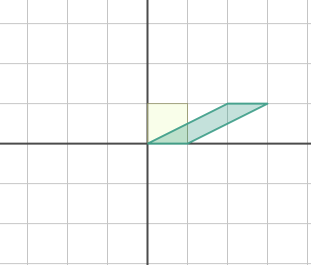
reflection

축 대칭
$M=\begin{bmatrix}-1&0\\0&1\\ \end{bmatrix}$

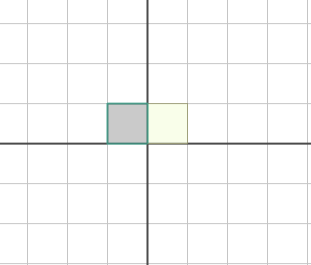
Translation

Affine Transformation에서 혼자서 linear하게 계산할 수 없는 친구이다.

그래서 변환을

$T(v) = v + u$와 같이 나타내야 하는데

이 때문에 Affine Transformation(Linear + Translation)을

$T(v) = M*v + u$와 같이 나타내야 한다.

수식의 아름다움, 일정함을 좋아하는 사람들이 심기가 불편했고

기발한 발상을 하게 된다.

!! 2차원 점을 translation 계산을 위한 요소를 하나 추가해 3차원 점으로 표시하면 translation도 linear하게 표현할 수 있다 !!

예를 들자면 $P=(1, 2)$라고 할 때
$v_P=(1,2,1)$ 와 같이 뒤에 1을 추가해 3차원 점으로 표기하는 것이다. (무조건 1을 추가한다.)

이렇게 된다면 원래 위의 변형도 그대로 사용할 수 있고

non-uniform scaling을 살펴보면

$M=\begin{bmatrix}2&0\\0&1\\ \end{bmatrix}$ 3*3 행렬로 변환

$M'=\begin{bmatrix}2&0&0\\0&1&0\\0&0&1\\ \end{bmatrix}$ 추가된 칸은 0으로 채운다. (마지막만 1로 표기)

$M'*v=\begin{bmatrix}2&0&0\\0&1&0\\0&0&1\\ \end{bmatrix}*\begin{bmatrix}1\\2\\1\\ \end{bmatrix}=\begin{bmatrix}2\\2\\1\\ \end{bmatrix}$

위와 같이 원래 $M=\begin{bmatrix}2&0\\0&1\\ \end{bmatrix}$을 곱하였을 때와 결과가 다르지 않아
추가된 1은 non-uniform scaling에 영향을 주지 않는다.

하지만 이 추가된 행과 열을 통해 Translation이 가능하다.

(x방향으로 3만큼 이동)

$M'=\begin{bmatrix}1&0&3\\0&1&0\\0&0&1\\ \end{bmatrix}$

$M'*v=\begin{bmatrix}1&0&3\\0&1&0\\0&0&1\\ \end{bmatrix}*\begin{bmatrix}1\\2\\1\\ \end{bmatrix}=\begin{bmatrix}4\\2\\1\\ \end{bmatrix}$

이와 같이 translation을 linear한 format으로 표현 가능하다.

$P=(1, 2)$를 $v_P=(1,2,1)$로 변환한
이러한 좌표를 Homogeneous Coordinate이라고 부른다.

Composition of Transformation

한 점에 대하여 여러 변환들이 적용이 될 때, 다음과 같이 표시할 수 있다.

$T(p) = M_T p$, $S(p) = M_S p$

$(S*T)(p)=S(T(p))=M_SM_Tp$

!! 이때 적용하는 순서에 따라 결과가 달라질 수 있음을 유의하자.

예시

rotation 후 shearing

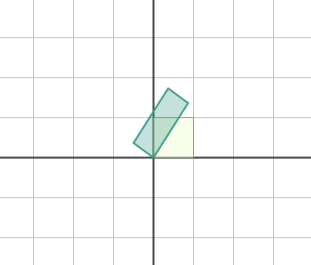
shearing 후 rotation