[Hackerrank 문제 풀이] Recursive Digit Sum (Super Digit)

Junu Kim·2025년 11월 21일

Java hackerrank

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

45/46

[Recursion] Recursive Digit Sum

난이도: ★★★☆☆ • solved on: 2025-11-21

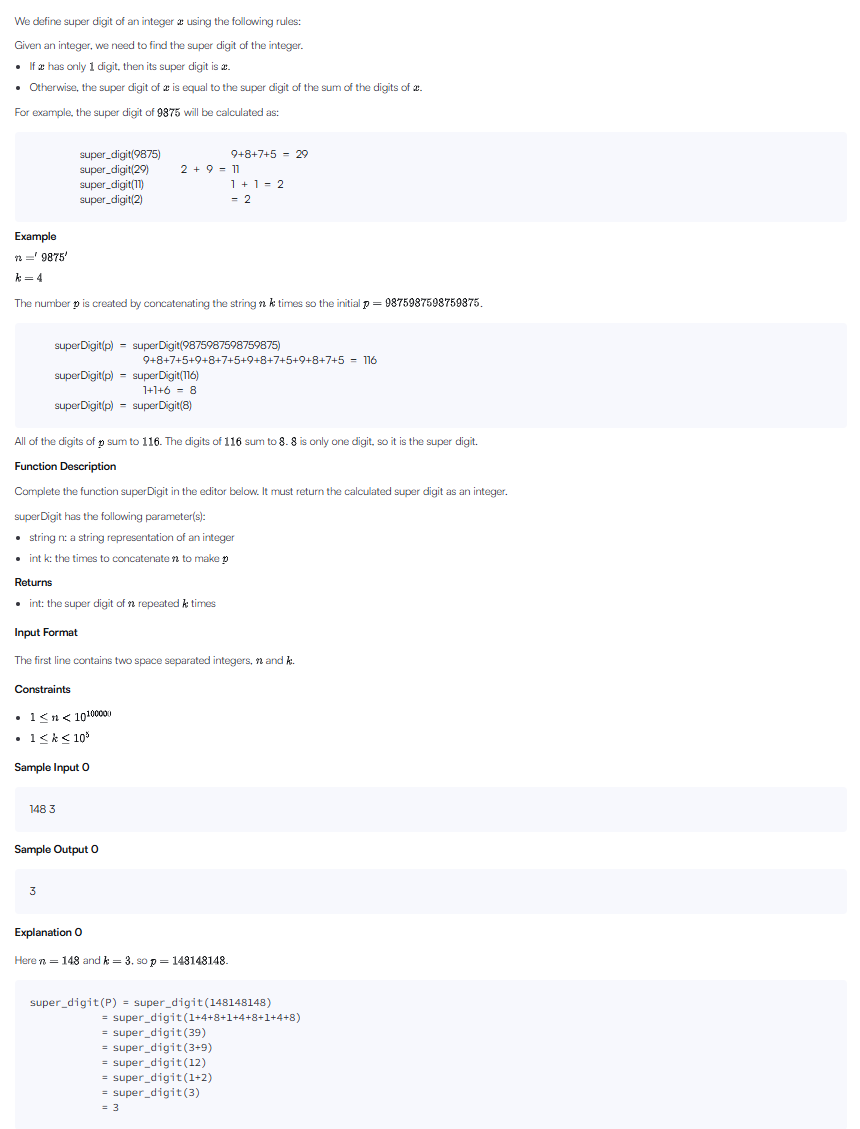
문제 요약

문제 유형: 재귀(recursion), 문자열 처리, 수학
요구사항: 문자열로 주어진 큰 수 n을 각 자릿수 합으로 줄여 단일 자릿수(super digit)로 만든다. 이때 주어진 k만큼 n을 반복해 합산한 값으로 시작해야 한다.

사용 개념

자료구조
- String, String[]
알고리즘/기법
- 재귀 호출(recursion)
- 자릿수 합(digit sum)
핵심 키워드
- super digit
- recursive reduction
- digit sum

풀이 아이디어

문제 분해

super digit은 “숫자를 자릿수 합으로 반복해서 단일 자릿수가 될 때까지 줄이는 작업”이다.

문제는 n을 문자열로 주기 때문에 정수 범위를 초과할 수 있다.

n을 k번 반복한 숫자를 직접 만드는 것은 비효율적이므로 sum(n) * k로 간접 계산한다.
핵심 로직 흐름
if 길이가 1이면 → 그대로 반환
else → 문자 하나씩 더해 자릿수 합 생성 후 재귀 호출
예외 처리

k가 적용되는 시점은 첫 번째 계산에서만 고려한다.

초대형 숫자를 직접 생성하지 않는다.

첫번째 풀이

public static int superDigit(String n, int k) {

    // Write your code here
    if(n.length() < 2){
        if(k==0){
            return Integer.parseInt(n);
        }
        int item = Integer.parseInt(n);
        item *= k;
        return superDigit(String.valueOf(item), 0);
    }

    String[] digits = n.split("");
    int result = 0;
    for(String s : digits){
        result += Integer.valueOf(s);
    }

    return superDigit(String.valueOf(result), k);
}

개선된 풀이 (효율 + 구조 명확화)

핵심 차이:

n이 매우 길 경우에도 안전하도록 long이나 BigInteger 대신 문자열 기반 합산 사용

k는 첫 호출에서만 적용

재귀 흐름이 더 직관적이고 조건이 단순함

코드량이 줄어 가독성이 높아짐

방법 설명

k가 1보다 크면 sum(n) * k 를 최초 한 번만 계산한다.
이후 super digit 계산은 단순히 “문자 합 → 재귀”로 진행한다.
단일 문자열 합산을 반복하므로 매우 큰 입력도 안정적으로 처리한다.

개선 코드

public static int superDigit(String n, int k) {
    // 첫 계산: n의 자릿수 합 × k
    long initialSum = 0;
    for (char c : n.toCharArray()) {
        initialSum += (c - '0');
    }
    initialSum *= k;

    return calcSuperDigit(initialSum);
}

private static int calcSuperDigit(long num) {
    if (num < 10) {
        return (int) num;
    }

    long sum = 0;
    while (num > 0) {
        sum += num % 10;
        num /= 10;
    }

    return calcSuperDigit(sum);
}