[Hackerrank 문제 풀이] Fibonacci Numbers

Junu Kim·2025년 11월 21일

Java hackerrank

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

44/46

[Recursion] Fibonacci Numbers

난이도: ★☆☆☆☆ • solved on: 2025-11-21

문제 요약

문제 유형: 재귀(Recursion), 수학, DP 기초
요구사항:
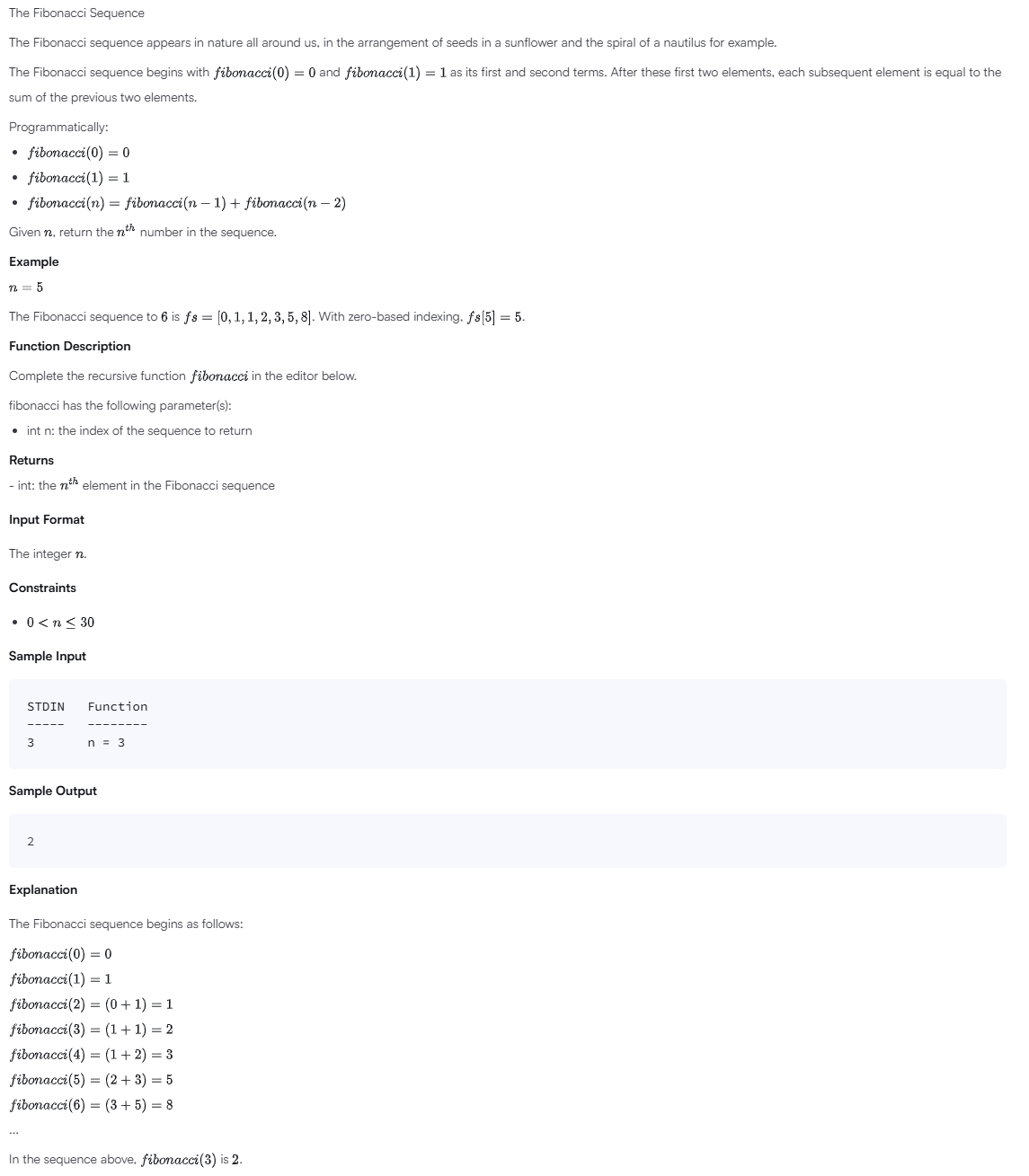
정수 n이 주어질 때, n번째 피보나치 수(F(n))를 계산한다.
정의:
- F(0) = 0
- F(1) = 1
- F(n) = F(n−1) + F(n−2)

사용 개념

자료구조
- 사용 없음 (순수 함수형 계산)
알고리즘/기법
- 재귀 호출(recursion)
- 점화식 기반 계산
핵심 키워드
- Dynamic Programming
- Memoization
- Recurrence Relation

풀이 아이디어

문제 분해

F(0), F(1)은 값이 고정되어 있으므로 즉시 반환한다.

나머지 n은 점화식 F(n) = F(n−1) + F(n−2)로 계산한다.
핵심 로직 흐름
if n == 0 → return 0
if n == 1 → return 1
return fibonacci(n-1) + fibonacci(n-2)
예외 처리

입력이 0 또는 1인 경우 즉시 반환하므로 문제가 없음.

코드

public class Solution {

    public static int fibonacci(int n) {

        // Complete the function.
        if(n==0){
            return 0;
        }
        
        if(n==1){
            return 1;
        }
        
        return fibonacci(n-1) + fibonacci(n-2);
        
    }
}

시간·공간 복잡도

시간 복잡도: O(2ⁿ)
(같은 부분 문제를 반복적으로 호출함)
공간 복잡도: O(n)
(재귀 호출 스택)

어려웠던 점

반복문 방식(iterative) 또는 메모이제이션을 사용할지 잠깐 고민했었다. 하지만 이번 문제는 Recursion을 활용해도 괜찮다 생각해 빠르게 구현했다.

배운 점 및 팁

재귀 풀이가 직관적이지만 비효율적이다.
같은 문제를 여러 번 호출하기 때문이다.
효율성을 높이려면 다음 두 가지 방식 중 하나를 사용하는 것이 일반적이다.
- 메모이제이션(Memoization) 적용
- 반복문(iterative) 기반 DP

Recursion을 대체하는 대표적인 로직

1. Iteration (반복문 방식, Bottom-Up DP)

가장 효율적이며 실무에서 가장 많이 사용한다.

아이디어

배열이나 변수 두 개만 사용해 F(0) → F(1) → F(2) … → F(n) 순서로 쌓아 올린다.

재귀 호출이 없기 때문에 스택 오버플로우 걱정이 없다.

특징

시간 복잡도: O(n)

공간 복잡도: O(1) (변수 2개)

가장 빠르고 메모리 효율적

2. Memoization (Top-Down DP, 재귀 + 캐싱)

재귀 기반이지만 중복 계산을 제거하여 매우 빠르게 만든다.

아이디어

fibonacci(n) 호출 시

이미 계산한 값은 배열이나 해시맵에 저장해두고

다시 호출되면 저장된 값을 바로 반환한다.

특징

시간 복잡도: O(n)

공간 복잡도: O(n) (메모 배열 + 재귀 스택)

재귀 구조를 유지하면서 속도만 개선하고 싶을 때 좋음