[Sort] Big Sorting

난이도: ★★☆☆☆ • solved on: 2025-12-11

---

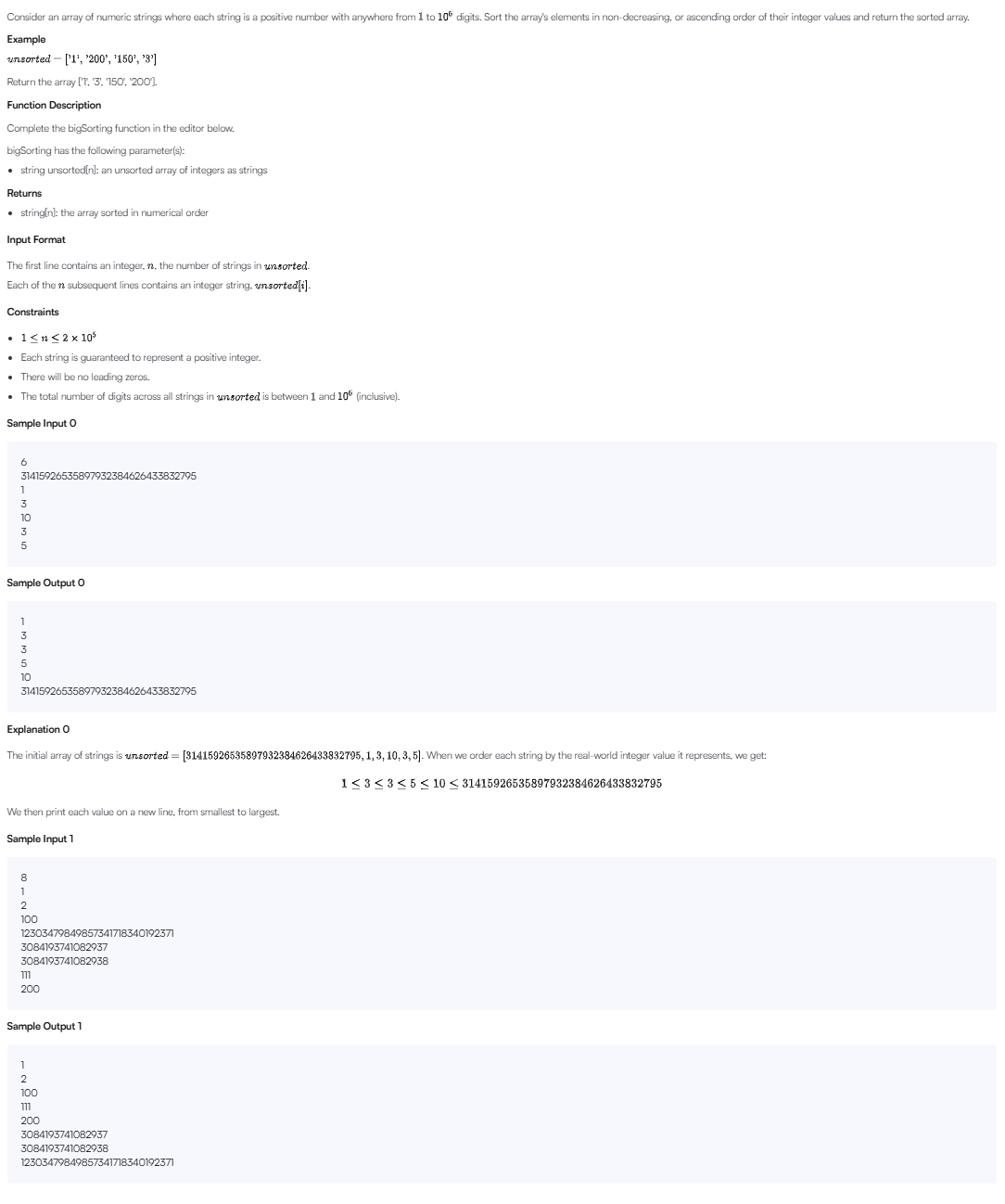
문제 요약

• 문제 유형: 정렬(Sorting), 문자열 처리

• 요구사항

  • 매우 큰 정수들이 문자열(String) 로 주어진다.
  • 이 수들을 정수값 기준 오름차순으로 정렬해야 한다.
  • 값의 크기가 long 범위를 넘어설 수 있어, 숫자형으로 변환해서 비교할 수 없다.
  • 따라서 문자열 길이 + 사전순 비교를 이용해 정렬 기준을 설계해야 한다.

---

사용 개념

1. 자료구조

   • List<String> : 입력 숫자들을 문자열로 저장
   • PriorityQueue<T> : 최소 힙(min-heap) 구현
   • Map<Integer, PriorityQueue<String>> : 길이 그룹별 힙 저장

2. 알고리즘/기법

   • Comparable / Comparator 활용
   • 문자열 길이 기반 정렬
   • 길이가 같을 때 lexicographical order(사전순) 비교

3. 핵심 키워드

   • 큰 수 정렬(large integer sorting)
   • 커스텀 정렬 기준(custom comparator)
   • 길이 우선 정렬(length-based sort)

---

풀이 아이디어 및 코드

방법 1 : CustomString + PriorityQueue 단일 힙 시도 (첫 시도)

전략

• CustomString 이라는 래퍼 클래스를 만들고, Comparable<CustomString> 을 구현한다.
• compareTo 에서 ...
  • 먼저 문자열 길이를 비교하고
  • 길이가 같으면 문자열 사전순으로 비교한다.

• 이렇게 하면 PriorityQueue<CustomString> 하나만 써도,
  • 항상 “가장 작은 수”가 힙의 top 에 오도록 만들 수 있다.

1. 핵심 로직

1) CustomString에 Comparable 구현
   - 길이 짧은 문자열이 더 작다.
   - 길이가 같으면 사전순으로 비교한다.

2) 모든 입력 문자열을 CustomString으로 감싸서 Min-Heap에 넣는다.

3) 힙에서 poll() 하면서 하나씩 꺼내 result 리스트에 data만 저장한다.

2. 코드 (원본 그대로)

public static class CustomString implements Comparable<CustomString>{
        String data;
        public CustomString(String data){
            this.data = data;
        }
    
        @Override
        public int compareTo(CustomString comparedString){
            if(this.data.length() < comparedString.data.length()){
                return -1;
            } else if(this.data.length() > comparedString.data.length()){
                return 1;
            } else {
                return this.data.compareTo(comparedString.data);
            }
        }
    }
    public static List<String> bigSorting(List<String> unsorted) {
        // Write your code here
        List<String> result = new ArrayList<>();
        PriorityQueue<CustomString> heap = new PriorityQueue<>();
        for(int i = 0; i < unsorted.size()-1; i++){
            heap.add(new CustomString(unsorted.get(i)));
        }
        for(int i = 0; i < unsorted.size(); i++){
            result.add(heap.poll().data);
        }
        return result;        
    }

3. 평가

• 시간 복잡도는 O(N log N × L) 로, 나중에 나올 정렬 풀이와 같은 오더이다.

---

방법 2 : 길이별 Map + PriorityQueue 조합 (두 번째 풀이)

의도

• 숫자 문자열의 길이를 key 로 하는 Map<Integer, PriorityQueue<String>> 를 만든다.

• 각 길이마다 문자열들을 PriorityQueue 에 넣으면,

  • 해당 길이 그룹 내부는 자동으로 사전순 정렬이 된다.

• 길이들(key)도 PriorityQueue<Integer> 에 넣어

  • 길이가 작은 그룹부터 차례대로 꺼내면서
  • 각 그룹의 PQ를 전체적으로 앞에서부터 빼서 결과 리스트에 쌓는다.

• 결국

  • "길이 오름차순" → "길이가 같은 구간 내부는 사전순" 이라는
  • 이 문제의 정렬 기준을 자료구조 레벨에서 그대로 흉내 낸 풀이이다.

1. 핵심 로직

1) for 각 문자열 item:
       len = item.length()
       mapQueue[len] 이 없으면 새 PriorityQueue 생성
       mapQueue[len].add(item)   // 같은 길이끼리 사전순으로 정렬되는 힙

2) for 각 길이 key in mapQueue.keySet():
       keyQueue.add(key)         // 길이들을 오름차순으로 관리

3) while keyQueue not empty:
       key = keyQueue.poll()     // 가장 짧은 길이부터
       while mapQueue[key] not empty:
           result.add(mapQueue[key].poll())  // 사전순대로 꺼냄

2. 코드 (원본 그대로)

public static List<String> bigSorting(List<String> unsorted) {
        // Write your code here
        List<String> result = new ArrayList<>();
        Map<Integer, PriorityQueue<String>> mapQueue = new HashMap<>();
        PriorityQueue<Integer> keyQueue = new PriorityQueue<>();
        for(String item: unsorted){
            if(!mapQueue.containsKey(Integer.valueOf(item.length()))){
                mapQueue.put(Integer.valueOf(item.length()), new PriorityQueue<>());
            }
            mapQueue.get(Integer.valueOf(item.length())).add(item);
        }
        for(Integer key : mapQueue.keySet()){
            keyQueue.add(key);
        }
        
        
        while(!keyQueue.isEmpty()){
            Integer key = keyQueue.poll();
            while(!mapQueue.get(key).isEmpty()){
                result.add(mapQueue.get(key).poll());
            }
        }
        return result;
              
    }

3. 평가

• 정렬 전략 자체는 완전히 맞다.

  • 길이 → 사전순 이라는 규칙을

    • “길이별 버킷 + 각 버킷 내부 PQ” 구조로 구현한다.

• 다만

  • Map, 다수의 PriorityQueue, keyQueue 까지 사용해 첫번째 시도에 비해서는 구조가 꽤 복잡하다.
  • 전체적인 시간 복잡도는 여전히 O(N log N × L) 수준이다.
    (각 PQ 삽입/삭제에 log 요인이 붙고, 문자열 비교 비용이 곱해진다.)

• 이 문제에서 요구하는 건

  • “자료구조를 복잡하게 짜는 것”보다
  • 정렬 기준(Comparator)을 잘 설계하는 것에 가깝기 때문에
  • 구현 난이도 대비 이득이 크지 않다.

---

방법 3 : 단일 리스트 + 커스텀 Comparator 정렬

핵심 전략

• 이 문제의 본질은

  • “정수로 바꿀 수 없는 큰 수를, 정수 크기 순서로 정렬하는 방법” 이다.

• 큰 수 비교 규칙은 다음 두 단계로 요약할 수 있다.

  1. 문자열 길이가 다르면

     • 길이가 더 짧은 수가 더 작은 수이다.

2. 길이가 같으면

   • 문자열을 사전순(lexicographical) 으로 비교하면
     → 실제 정수 크기 비교와 동일해진다.

• 이 규칙을 람다 함수를 활용해 Comparator<String>으로 한 번만 정의해서

  • unsorted.sort(comparator) 로 정렬하면
  • 별도의 Map, PQ 없이 문제를 해결할 수 있다.

1. 핵심 로직

unsorted.sort( (a, b) -> {
    if (a.length() != b.length())
        return a.length() - b.length();  // 자리수가 적은 수가 더 작다.
    return a.compareTo(b);               // 길이가 같을 때 사전순
});

return unsorted;

2. 코드 (최종 권장 풀이)

import java.util.*;

public class Solution {

    public static List<String> bigSorting(List<String> unsorted) {
        // "정수값" 기준을 문자열 길이 + 사전순으로 표현하는 Comparator
        unsorted.sort((a, b) -> {
            int lenA = a.length();
            int lenB = b.length();

            if (lenA != lenB) {
                return lenA - lenB;              // 길이가 짧은 수가 더 작다
            }
            return a.compareTo(b);               // 길이가 같으면 사전순 비교
        });

        return unsorted;
    }
}

---

시간·공간 복잡도

방법 1 : CustomString + PriorityQueue 단일 힙

• 시간 복잡도

  • N개의 원소를 힙에 넣고(add) 다시 빼는(poll) 과정 → O(N log N)
  • 각 비교에서 길이가 같을 경우 문자열 비교 비용 최대 O(L)
  • 전체적으로 O(N log N × L)

• 공간 복잡도

  • CustomString 래퍼 객체 + 힙 내부 저장 공간 → O(N)

방법 2 : Map + PriorityQueue(여러 개) + keyQueue

• 시간 복잡도

  • 각 문자열을 길이 그룹 PQ에 삽입: O(N log N) 수준
  • 각 그룹 PQ에서 poll 하며 result에 삽입: O(N log N)
  • 비교 비용 포함 시 O(N log N × L)

• 공간 복잡도

  • 길이별 PQ + keyQueue + Map → 여전히 O(N)

방법 3 : List + Comparator 정렬

• 시간 복잡도

  • 정렬 알고리즘(TimSort)의 비교 횟수: O(N log N)
  • 각 비교에 드는 비용: 길이 비교 O(1), 길이가 같을 때 문자열 비교 O(L)
  • 따라서 O(N log N × L)
  • 이론상 다른 방법들과 같은 오더지만, 구현이 단순하여 상수 시간·메모리 오버헤드가 작다.

• 공간 복잡도

  • 정렬용 보조 버퍼 외에는 별도 자료구조 필요 없음 → O(N) 이하

---

어려웠던 점

• 처음에는

  • “힙을 쓰면 알아서 정렬된 순서로 빠져나오니까 PriorityQueue로 날먹할 수 있지 않을까?”라는 생각으로 접근했으나,
  • 구현 도중 루프 범위(off-by-one) 를 잘못 잡아 마지막 원소가 누락되는 버그가 발생했다. 하지만 이 원인을 처음에는 인지하지 못해 접근이 잘못되었나? 하고 다음 접근인 방법2로 넘어갔다 (디버깅을 더 열심히 해보자)

• 두 번째 풀이에서는

  • 길이별 Map + PQ 구조를 설계하면서
  • 정렬 기준 자체를 자료구조 레벨에서 표현하는 데 성공했지만,
  • 코드 구조가 복잡해지고, 핵심인 “비교 전략” 자체가 뿔뿔이 흩어져버리는 느낌이 있었다.

• 결국 이 문제는 어떤 자료구조를 쓰느냐보다, “정렬 기준을 어떻게 설계하느냐”가 핵심임을 깨닫게 된다.

---

배운 점 및 팁

• 큰 수 정렬 문제에서 기본 전략은 다음과 같이 기억해두면 좋다.

  1. 길이 비교: 자리수가 적은 수가 항상 더 작다.

  2. 길이가 같으면 문자열 사전순: 정수 비교와 동일한 결과를 보장한다.

• Java에서 정렬 문제에 부딪혔을 때:

  • “자료구조로 해결해야 할까?” 를 고민하기 전에

  • Comparator 하나로 해결 가능한지 먼저 생각하는 습관을 들이는 것이 좋다.

• Comparable vs Comparator

  • Comparable: 클래스 자체에 “기본 정렬 기준”을 넣고 싶을 때

  • Comparator:

    • 한 클래스에 여러 정렬 기준이 필요하거나
    • 기존 클래스(String 등)에 외부에서 정렬 기준을 입히고 싶을 때 사용한다.

• PriorityQueue는

  • “항상 가장 작은/큰 원소 하나를 빠르게 뽑아야 하는 상황”에 강점이 있고, 단순히 전체 정렬만 필요할 때는 정렬 API(내장 sort) 가 더 직관적이고 간단하다.

---

참고 및 링크

• 문제 링크: Big Sorting – HackerRank
• 참고 블로그/깃허브: Java Priority Queue(우선순위 큐)와 Comparable, Comparator – velog

---

추가 연습 문제

• 비슷한 유형 (GPT 추천)

  • Sorting: Comparator
  • 시리얼 번호

• 확장 문제 (GPT 추천)

  • 소트인사이드
  • Big Sorting