[Hackerrank 문제 풀이] QHEAP1 – Min Heap 구현

Junu Kim·2025년 12월 10일

Java hackerrank

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

55/89

[Heap] QHEAP1 – Min Heap 구현

난이도: ★★☆☆☆ • solved on: 2025-12-10

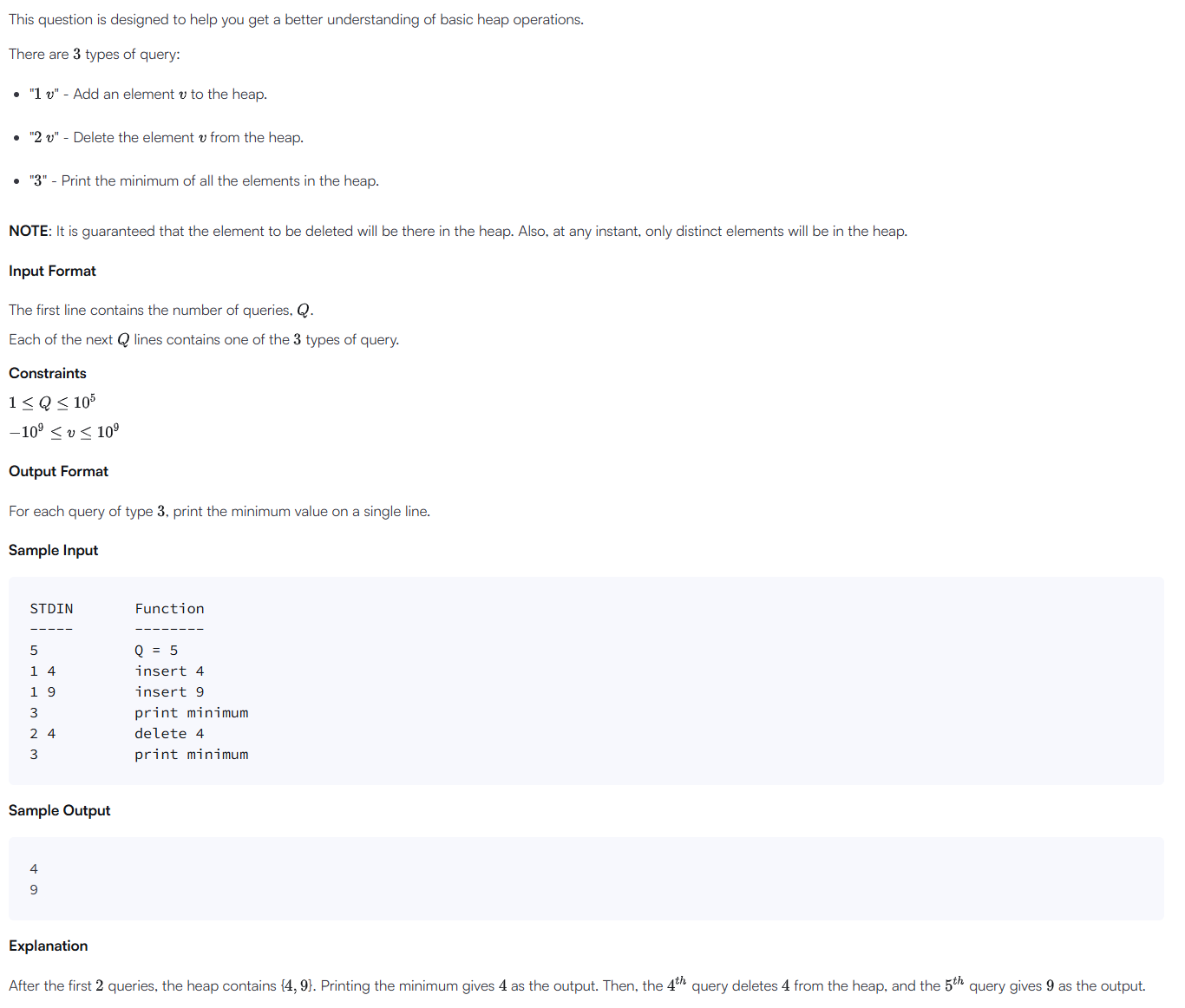
문제 요약

문제 유형: 자료구조, 힙(Heap), 우선순위 큐
요구사항
다음 세 가지 쿼리를 효율적으로 처리해야 한다.
1. 1 x : 정수 x를 집합에 삽입
2. 2 x : 정수 x를 집합에서 삭제
3. 3 : 현재 집합에 있는 값들 중 최솟값을 출력

힙(특히 Min Heap)을 이용해 위 연산들을 구현하는 문제이다.

사용 개념

자료구조
- ArrayList<Integer>
  - 완전 이진 트리(Complete Binary Tree)를 배열로 표현하기 위해 사용
  - 인덱스 i 기준
    - 왼쪽 자식: 2 * i + 1
    - 오른쪽 자식: 2 * i + 2
    - 부모: (i - 1) / 2
알고리즘/기법
- Min Heap 삽입 (sift up / heapify up)
- Min Heap 재정렬 (sift down / heapify down)
- 입력 최적화: BufferedReader 사용
핵심 키워드
- Min Heap, 완전 이진 트리
- siftUp / siftDown
- 우선순위 큐(Priority Queue)

풀이 아이디어

Min Heap으로 값 관리

배열 기반 힙을 직접 구현한다.

항상 루트 인덱스(0) 에 최솟값이 오도록 유지한다.
핵심 로직 흐름
insert(x):
    1) heap 맨 뒤에 x 추가
    2) 새로 들어간 인덱스에서 부모와 비교하며 위로 올림 (siftUp)

deleteValue(x):
    1) heap에서 값이 x인 인덱스를 선형 탐색으로 찾음
    2) 찾은 위치를 마지막 원소와 교체 후 마지막 원소 제거
    3) 부모보다 작은지 / 자식보다 큰지에 따라
       - 위로 올릴지(siftUp) / 아래로 내릴지(siftDown) 결정

getMin():
    - heap.get(0) 을 그대로 반환
예외 처리 및 구현 포인트

deleteValue(x)에서 값이 존재하지 않으면 바로 반환

삭제 시, 마지막 원소를 가져온 위치에서

부모보다 작으면 siftUp

그렇지 않으면 siftDown

입력은 BufferedReader로 한 줄씩 읽어 쿼리 타입에 따라 분기

코드

import java.io.*; 
import java.util.*; 

public class Solution { 
    
    static class MinHeap { 
        ArrayList<Integer> heap = new ArrayList<>(); 
        
        int size() { 
            return heap.size(); 
        } 
        
        void swap(int i, int j) { 
            int tmp = heap.get(i); 
            heap.set(i, heap.get(j)); 
            heap.set(j, tmp); 
        } 
        
        void siftUp(int i) { 
            while (i > 0) { 
                int p = (i - 1) / 2; 
                if (heap.get(p) <= heap.get(i)) break; 
                swap(p, i); 
                i = p; 
            } 
        } 
        
        void siftDown(int i) { 
            int n = heap.size(); 
            while (true) { 
                int left = 2 * i + 1; 
                int right = 2 * i + 2; 
                int smallest = i; 
                
                if (left < n && heap.get(left) < heap.get(smallest)) { 
                    smallest = left; 
                } 
                if (right < n && heap.get(right) < heap.get(smallest)) { 
                    smallest = right; 
                } 
                
                if (smallest == i) break; 
                
                swap(i, smallest); 
                i = smallest; 
            } 
        } 
        
        void insert(int x) { 
            heap.add(x); 
            siftUp(heap.size() - 1); 
        } 
        
        int getMin() { 
            return heap.get(0); 
        } 
        
        void deleteValue(int x) { 
            int n = heap.size(); 
            int idx = -1; 
            for (int i = 0; i < n; i++) { 
                if (heap.get(i) == x) { 
                    idx = i; 
                    break; 
                } 
            } 
            if (idx == -1) return; 
            
            int lastIdx = n - 1; 
            if (idx == lastIdx) { 
                heap.remove(lastIdx); 
                return; 
            } 
            
            int lastVal = heap.get(lastIdx); 
            heap.set(idx, lastVal); 
            heap.remove(lastIdx); 
            
            if (idx > 0 && heap.get(idx) < heap.get((idx - 1) / 2)) { 
                siftUp(idx); 
            } else { 
                siftDown(idx); 
            } 
        } 
    } 
    
    public static void main(String[] args) throws IOException { 
        BufferedReader br = new BufferedReader( 
            new InputStreamReader(System.in) 
        ); 
        int q = Integer.parseInt(br.readLine()); 
        MinHeap heap = new MinHeap(); 
        
        for (int i = 0; i < q; i++) { 
            String line = br.readLine(); 
            while (line != null) { 
                String[] cmds = line.split(" "); 
                int type = Integer.parseInt(cmds[0]); 
                
                if (type == 1) { 
                    int x = Integer.parseInt(cmds[1]); 
                    heap.insert(x); 
                } else if (type == 2) { 
                    int x = Integer.parseInt(cmds[1]); 
                    heap.deleteValue(x); 
                } else if (type == 3) { 
                    System.out.println(heap.getMin()); 
                } 
                
                line = br.readLine(); 
            } 
        } 
    } 
}

시간 및 공간 복잡도

삽입 insert(x)
- siftUp 때문에 시간 복잡도: O(log N)
최솟값 조회 getMin()
- 루트 접근 한 번이므로 시간 복잡도: O(1)
값 삭제 deleteValue(x)
- 선형 탐색으로 인덱스 찾기: O(N)
- 이후 siftUp 또는 siftDown: O(log N)
- 전체적으로 시간 복잡도: O(N)
공간 복잡도
- 힙에 저장된 원소 개수를 N이라 할 때: O(N)

어려웠던 점

heap의 insert, siftUp, siftDown을 직접 구현하는 구조를 잡는 데 시간이 많이 들었다.
배열 인덱스로 부모/자식 관계를 계산하는 방식이 바로 떠오르지 않아, 구조체(클래스)를 어떻게 짤지 고민이 컸다.
결국 인터넷 자료를 찾아보고, GPT에게도 물어보면서 힙 구조 자체를 이해한 뒤 구현을 완성했다.
솔직히, Queue로만 풀라면 금방 할 수 있을 것 같은데, 굳이 Heap을 직접 구현해야 하는 이유가 체감이 잘 되지 않아 더 어렵게 느껴졌다.

배운 점 및 팁

Min Heap은 “항상 루트가 최솟값”이 되도록 부모 ≤ 자식 관계를 유지하는 완전 이진 트리라는 점을 다시 한 번 정리할 수 있었다.
siftUp, siftDown은 결국
- 부모보다 작으면 위로 올리고
- 자식보다 크면 아래로 내린다
  라는 단순한 규칙으로 이해하면 구현이 한결 쉬워진다.
실제 코딩 테스트나 실무에서는 PriorityQueue를 쓰면 되고, 이번 풀이는 Min Heap을 직접 구현하면서 연습해본 풀이이다.