[Hackerrank 문제 풀이] Height of a Binary Tree

Junu Kim·2025년 12월 5일

Java hackerrank

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

51/89

[Tree] Height of a Binary Tree

난이도: ★★☆☆☆ • solved on: 2025-12-05

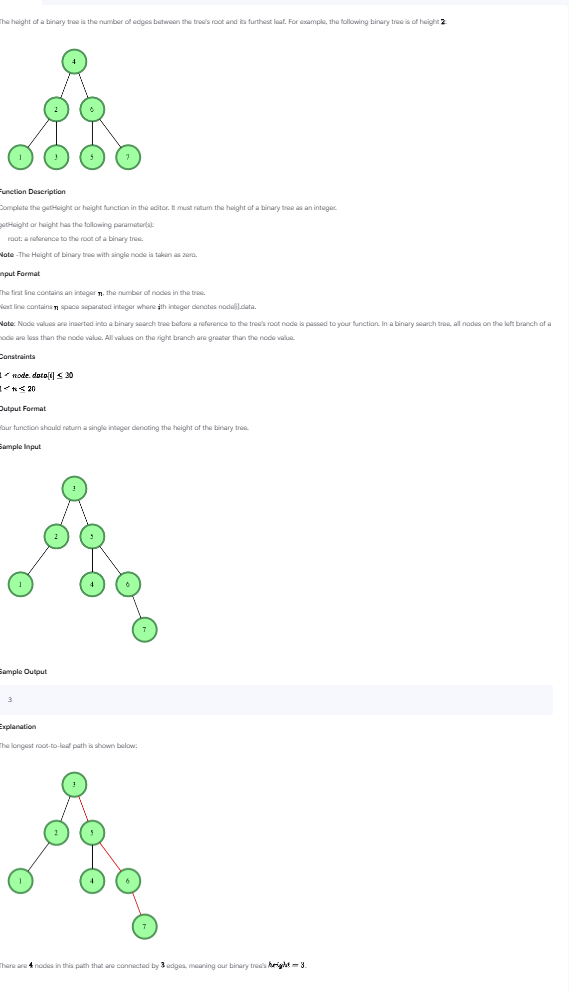
문제 요약

문제 유형: 트리(Tree), DFS
요구사항: 이진 트리의 height(높이) 를 계산해야 한다. height는 root에서 leaf까지의 edge 수로 정의된다.

사용 개념

자료구조
- Binary Tree(Node 구조)
알고리즘/기법
- DFS(재귀)
- 분할 정복(divide and conquer)
핵심 키워드
- height 계산
- leaf 처리
- edge count 기반 정의

풀이 아이디어 및 코드

방법 1 : child 존재 여부 기반 height 증가 방식

문제 분해

height 증가 시점을 명확하게 잡기 어렵다고 판단하여,
“child가 있으면 +1, 없으면 0으로 전환”하는 방식을 채택했다.

기본값을 1로 두고, 자식이 없는 경우 height를 0으로 조정한다.

핵심 로직 흐름
if root == null → 0
tmpLeft = 1, tmpRight = 1
왼쪽 자식이 있으면 height(left) 더하기
없으면 tmpLeft = 0

오른쪽 동일 처리

return max(tmpLeft, tmpRight)
예외 처리

자식이 없는 leaf 노드는 height = 0

null root height = 0

public static int height(Node root) {
    if (root == null) {
        return 0;
    }

    int tmpLeft = 1;
    int tmpRight = 1;
    int tmpRoot = 0;

    if (root.left != null) {
        tmpLeft += height(root.left);
    } else {
        tmpLeft = 0;
    }

    if (root.right != null) {
        tmpRight += height(root.right);
    } else {
        tmpRight = 0;
    }

    return tmpRoot + Math.max(tmpLeft, tmpRight);
}

방법 2 : 개선된 정석 DFS 풀이 (max(left, right) + 1)

문제 분해

트리 height = “두 서브트리의 height 중 큰 값 + 1”

leaf 노드의 height는 0

null 노드는 height = 0 으로 처리하면 HackerRank 기준과 일치한다.

핵심 로직 흐름
if root is null: return 0
left = height(root.left)
right = height(root.right)
return max(left, right) + 1
예외 처리

root가 null → height = 0

leaf 노드는 left=right=0 → height = 1?
HackerRank에서는 leaf height = 0이므로 위 수식을 기반으로 0을 유지한다.

public static int height(Node root) {
    if (root == null) {
        return 0;
    }

    int left = height(root.left);
    int right = height(root.right);

    return Math.max(left, right) + 1;
}

시간·공간 복잡도

방법 1

시간 복잡도: O(N)
공간 복잡도: O(H)

방법 2

시간 복잡도: O(N)
공간 복잡도: O(H)

두 방식 모두 DFS 기반이므로 동일한 복잡도를 가진다. 하지만 가독성 면에서 방법 2가 압도적으로 좋다

어려웠던 점

레벨 단위로 BFS를 먼저 떠올렸으나, height를 edge count로 세는 구조와 맞지 않아 DFS로 전환했다.
height 증가 시점을 어디에 두어야 하는지 감이 잡히지 않아 여러 구조를 시도했다.
leaf 여부를 조건으로 height 조정하는 방식(tmpLeft 기본값을 1로 두고 없으면 0으로 변경)이 그 당시 문제 해결에는 유용했지만, 이후 더 단순한 공식(max+1)이 존재함을 알게 되었다.