[1193] 분수찾기

난이도: ★★★★☆ • solved on: 2025-07-09

---

문제 요약

• 문제 유형: 구현, 수학
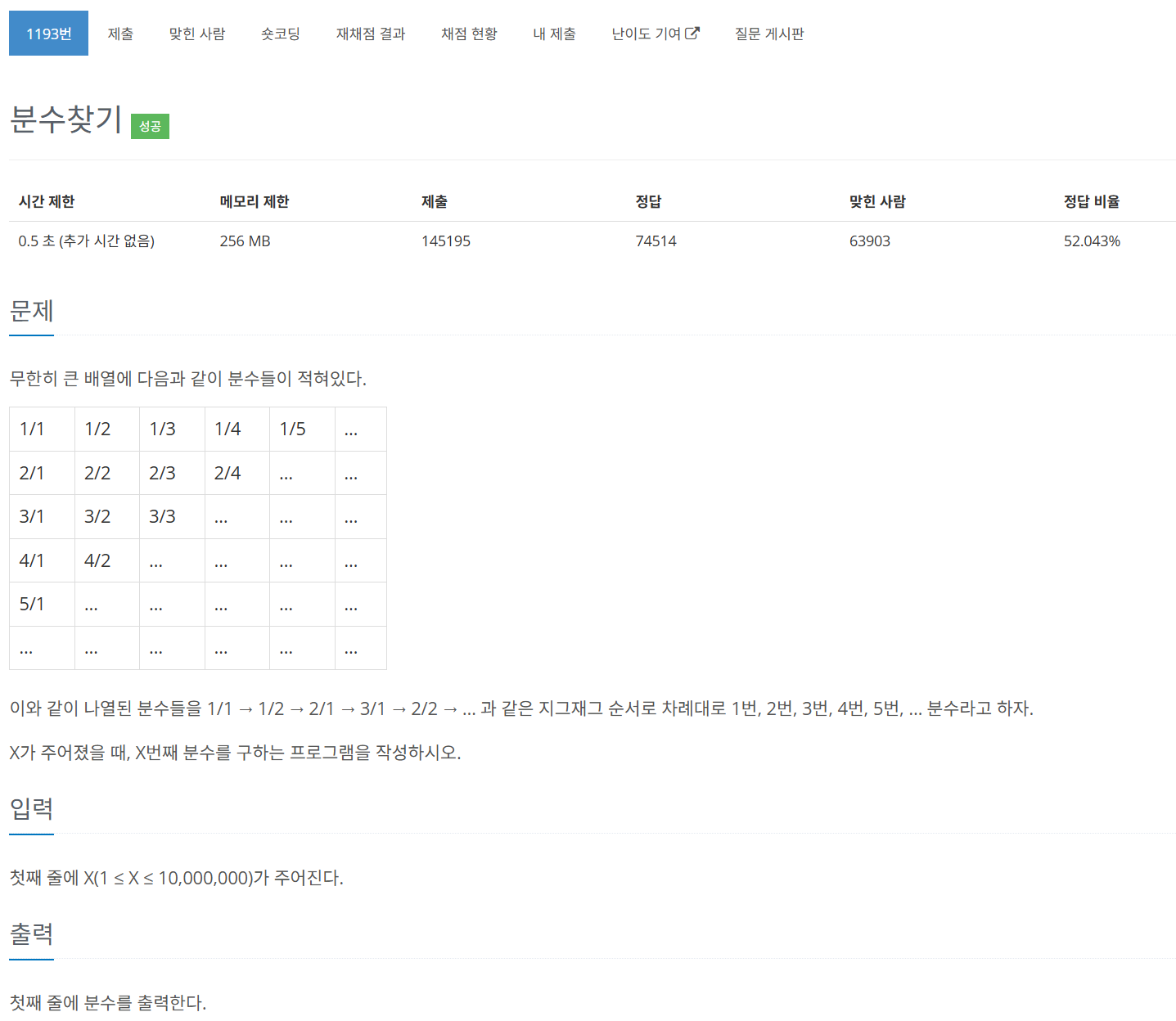
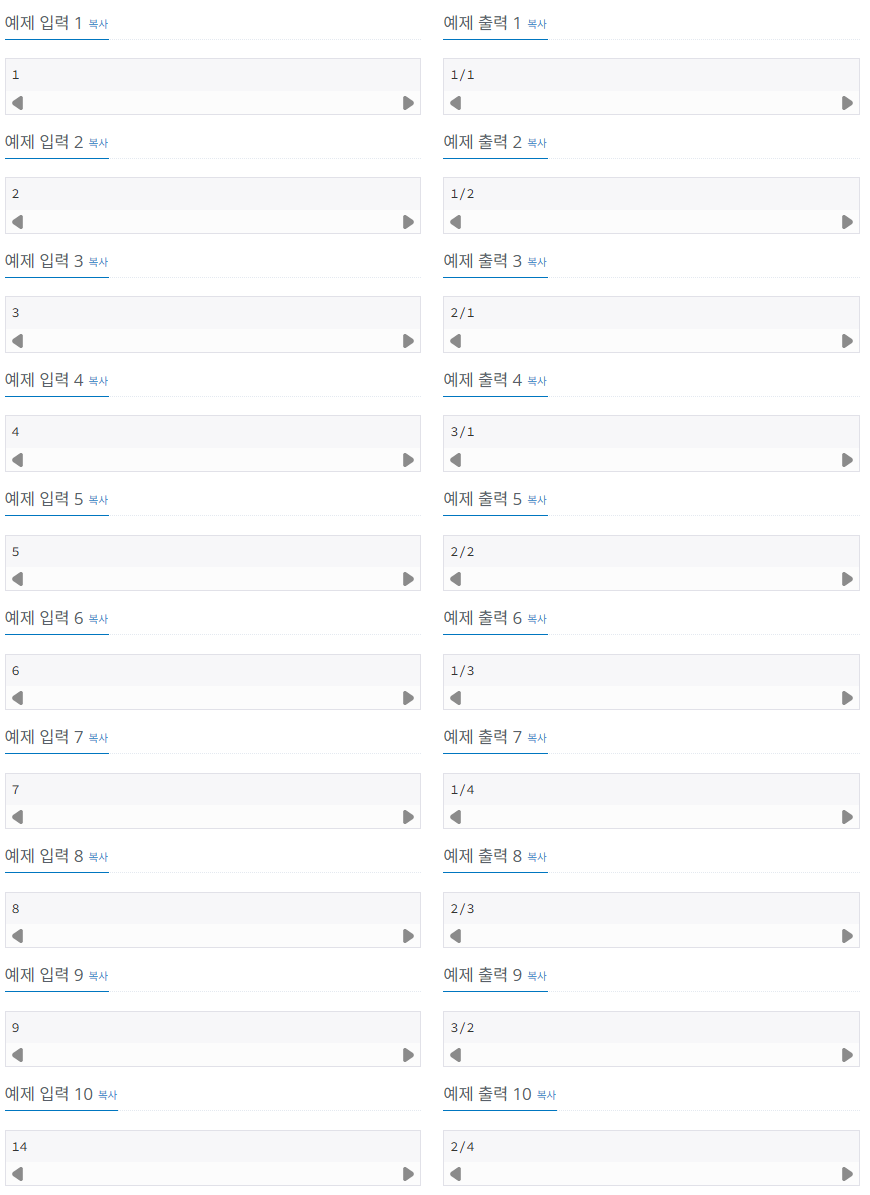
• 요구사항: 입력값 N이 주어졌을 때, N번째 분수를 “X/Y” 형태로 출력해야 한다.

---

사용 개념

1. 자료구조
   • 단순 변수 (int), 배열 (위치 추적)
2. 알고리즘/기법
   • 패턴 규칙성 분석, 누적합, 구현
3. 핵심 키워드
   • 지그재그 대각선 탐색, 삼각수(triangular number), 위치 패턴, 구현

---

풀이 아이디어 및 코드

방법 1 : 시뮬레이션 (직접 움직이며 위치 추적, for문 N번)

1. 문제 분해
   • 시작을 1/1에서 시작, 대각선을 따라 지그재그로 움직임
   • 방향 전환(↗, ↙)은 분자가 1이거나 분모가 1일 때 발생
   • 반복문으로 한 칸씩 이동하며 N번째 위치에 도달할 때까지 수행
2. 핵심 로직 흐름

   axis = [1,1]
   for i in 1~N-1:
       if axis[0]==1 and isEdge:
           axis[1]+=1; isEdge=false; isUp = !isUp; continue
       if axis[1]==1 and isEdge:
           axis[0]+=1; isEdge=false; isUp = !isUp; continue
       if isUp:
           axis[0]-=1; axis[1]+=1; if(axis[0]==1) isEdge=true
       else:
           axis[0]+=1; axis[1]-=1; if(axis[1]==1) isEdge=true
   ``

3. 예외 처리
   • N=1인 경우 1/1 바로 출력

import java.util.*;
import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[] axis = {1,1};
        boolean isEdge = true;
        boolean isUp = true;
        if(n>1){
            for(int i = 0; i < n-1; i++){
                if(axis[0]==1&&isEdge){
                    axis[1]+=1;
                    isEdge = false;
                    isUp = !isUp;
                    continue;
                }
                if(axis[1]==1&&isEdge){
                    axis[0]+=1;
                    isEdge = false;
                    isUp = !isUp;
                    continue;
                }
                if(isUp){
                    axis[0]-=1;
                    axis[1]+=1;
                    if(axis[0]==1){
                        isEdge = true;
                    }
                } else{
                    axis[0]+=1;
                    axis[1]-=1;
                    if(axis[1]==1){
                        isEdge = true;
                    }
                }
            }
        }
        System.out.println(axis[0]+"/"+axis[1]);
    }
}

---

방법 2 : 규칙성 및 수학적 공식(삼각수 활용, O(√N) 탐색)

1. 문제 분해

• 각 대각선(1, 2, 3, ...)에는 대각선 번호만큼의 원소가 들어감(1개, 2개, 3개 ...)
• N이 포함된 대각선 번호(line)을 찾는다. (삼각수 공식 이용)
• line번째 대각선의 시작 위치 = (line-1)*line/2 + 1
• 방향: line이 짝수면 (아래→위), 홀수면 (위→아래)
• 분자/분모는 line과 N의 상대적 위치로 바로 계산

2. 핵심 로직 흐름

   sum = 0, line = 0
   while (sum < N): sum += ++line
   offset = N - (sum - line)
   if line % 2 == 0:
       분자 = offset, 분모 = line - offset + 1
   else:
       분자 = line - offset + 1, 분모 = offset

3. 예외 처리
   • N=1일 때 1/1 바로 출력

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        int line = 0;
        int sum = 0;

        // N이 위치한 대각선(line) 찾기
        while (sum < N) {
            line++;
            sum += line;
        }

        int offset = N - (sum - line); // 그 대각선에서 몇 번째인지

        int numerator, denominator;
        if (line % 2 == 0) {
            numerator = offset;
            denominator = line - offset + 1;
        } else {
            numerator = line - offset + 1;
            denominator = offset;
        }
        System.out.println(numerator + "/" + denominator);
    }
}

---

시간·공간 복잡도

방법 1:

• 시간 복잡도 : O(N)
• 공간 복잡도 : O(1)

방법 2:

• 시간 복잡도 : O(√N) (대각선 번호 탐색)
• 공간 복잡도 : O(1)

---

어려웠던 점

• 지그재그로 움직이기에 움직이는 방향, N과 분수와의 관계에 대한 규칙성을 찾는 과정이 직관적이지 않았다.
• 각 분수 위치가 대각선 번호와 어떤 수학적 관계가 있는지 명확히 이해하는 것이 어려웠다.
• 그래서 규칙성보다는 반복문을 통한 시뮬레이션으로 먼저 접근했다.

---

배운 점 및 팁

• 삼각수(1+2+3+...+n) 공식을 이용하면 N이 어느 대각선에 속하는지 빠르게 찾을 수 있다.
• 방향(대각선의 짝수/홀수)에 따라 분자/분모가 바뀌므로 if문을 통한 처리만 하면 반복문 없이 O(√N) 시간에 바로 답을 구할 수 있다.
• 패턴 관찰 + 수학적 공식 결합이 구현보다 훨씬 효율적이었다.

---

참고 및 링크

• 문제 링크: https://www.acmicpc.net/problem/1193
• 참고 블로그/깃허브: 없음

---

추가 연습 문제

• 비슷한 유형 (GPT 추천) :

  • [2628] 종이자르기 (위치 추적, 시뮬레이션)
  • [1011] Fly me to the Alpha Centauri (패턴, 수열, 규칙 찾기)

• 확장 문제 (GPT 추천) :

  • N번째 삼각수 혹은 대각선 패턴이 등장하는 문제에서 일반항 공식 유도
  • N이 주어진 좌표평면에서 특정 패턴(예: 달팽이, 대각선, 지그재그)으로 번호를 매기는 문제