[백준 문제 풀이] 2292번 벌집

Junu Kim·2025년 7월 6일

Java baekjoon boj

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

12/46

[2292] 벌집

난이도: ★★★★☆ • solved on: 2025-07-06

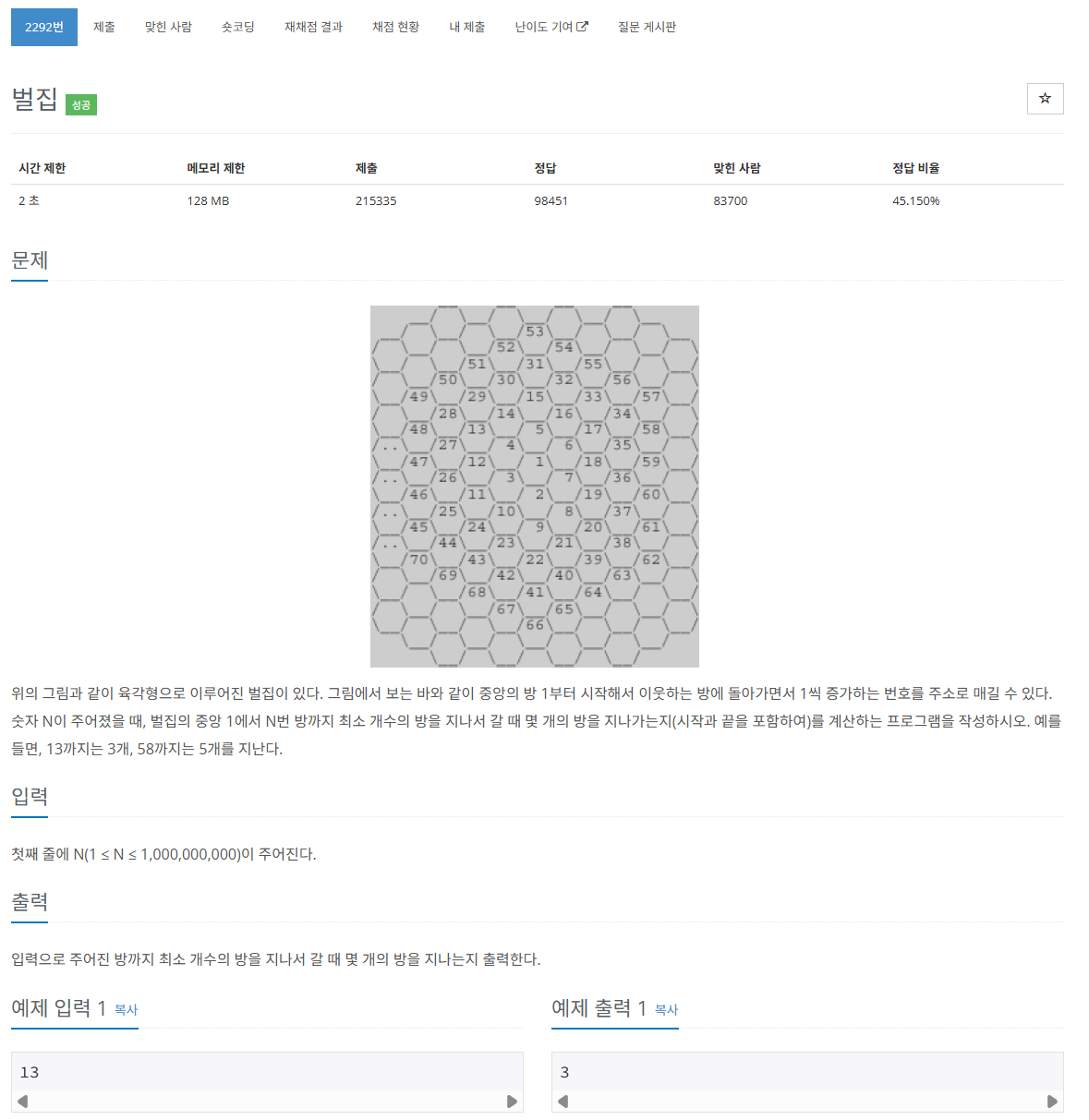
문제 요약

문제 유형: 수학, 구현
요구사항: 주어진 방 번호까지 최소 몇 개의 방을 지나가야 도달할 수 있는지 구해야 한다. (중앙 1번 방에서 시작)

사용 개념

자료구조
- 없음 (단순 변수, 반복문)
알고리즘/기법
- 계차수열
- 반복문, 수식 유도
핵심 키워드
- 계차수열, 범위 규칙 찾기, 수학적 귀납

풀이 아이디어 및 코드

방법 1 : 수식 전개 없이 반복문 사용

문제 분해

각 층에서 추가되는 방의 수는 6의 배수로 증가(6, 12, 18, …).

n번 방이 몇 번째 층에 포함되는지 반복문으로 찾는다.
핵심 로직 흐름
1. n = 1이면 바로 1 리턴
2. 각 층의 범위(3*i*(i-1)+1)에 대해 n이 어디에 속하는지 i를 1부터 증가시키며 찾기
예외 처리

n = 1일 때: 바로 1 출력

import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        if(n==1){
            System.out.print(1);
        }
        for(int i = 1; i <= n; i++){
            if(n<=3*i*(i-1)+1&&n>3*(i-1)*(i-2)+1) {
                System.out.print(i);
                break;
            }
        }
    }
}

방법 2 : 수식만으로 층(레벨) 계산 (O(1) 근사)

문제 분해

벌집의 각 층의 마지막 번호는 1 + 6 × (1+2+...+(k-1)) = 3k(k-1)+1

이 식을 k에 대해 풀면, 주어진 n에 대해 최소 k를 빠르게 찾을 수 있음
핵심 로직 흐름
1. k에 대해 3k^2 - 3k + 1 >= n 을 만족하는 최소 k를 찾는다.
2. 수학적으로 풀면 k = ceil((sqrt(12*(n-1)+9)-3)/6)
예외 처리

n = 1일 때는 바로 1 리턴

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        if(n == 1) {
            System.out.println(1);
            return;
        }
        int k = (int)Math.ceil((Math.sqrt(12 * (n-1) + 9) - 3) / 6);
        System.out.println(k);
    }
}

시간·공간 복잡도

방법 1 :

시간 복잡도: O(√N) (i가 빠르게 커짐)

공간 복잡도: O(1)

방법 2 :

시간 복잡도: O(1) (수식 한 번 계산)

공간 복잡도: O(1)

어려웠던 점

벌집 방의 규칙성(계차수열 구조, 6의 배수 누적)의 패턴을 처음에 바로 찾지 못했다.
for문에서 조건을 i < n으로 실수해 정답이 잘 안 나왔다. i <= n으로 모든 경우를 다 커버해야 했다.

배운 점 및 팁

반복문보다 수식 전개로 풀이를 빠르게 만들 수 있다 (특히 O(1) 근사).
[ 과거 중고등학교에 배운 방정식을 더 활용해보자.]
반복문 조건(<=, < 등) 실수는 항상 작은 케이스를 직접 손으로 대입하며 검증해야 한다.
규칙적인 증가 (특히 등차, 계차수열)는 식을 직접 써보면서 범위를 구체적으로 분석하면 쉽게 공식을 유도할 수 있다.
계차수열 (階差數列)
각 항들 사이의 '차'로 이루어진 수열(즉, 차분(差分) 수열)이 등차수열이 되는 수열을 말함. 즉, 앞뒤 항의 차들이 일정하게 증가(또는 감소)하는 패턴.
- 대표 예시:
  1, 7, 19, 37, 61, ...
  (각 항의 차이: 6, 12, 18, 24, ... → 6씩 증가)