아직 학생이기도하고 영어가 미숙하다보니 본 리뷰에 오류가 있을 수도 있습니다. 이 점 감안해주시고 혹시나 찾으신다면 피드백 감사히 받겠습니다.

요즘 학교 졸업작품때문에 평소 관심있던 주제인 3D Vision과 Generative Model중에서 GAN 쪽에 시간 투자를 많이 하고 있습니다. 그러던 중 Transformer와 관련된 GAN 쪽에 관심이 생겨서 관련 논문을 많이 읽어보려 하고 있는데요. 이번 포스팅에는 Transformer까지는 아니지만 그래도 Attention mechanism을 GAN에 적용시킨 논문인 SAGAN(Self-Attention Generative Adversarial Networks)에 대해서 리뷰해보려고 합니다.

1. Introduction

늘 그렇다시피, 이미지 생성된 연구중에서는 GAN이 꾸준히 좋은 성능을 내고 있어왔다는 내용으로 시작합니다. 하지만 당시 GAN이 좋은 성능을 내기는 하지만 아직은 기하학적이고 구조적인 패턴에 대해서는 잘 생성하지 못한다는 문제점을 갖고 있다고 합니다. 그 예시로 강아지의 이미지를 생성해낼 때 강아지의 털 패턴과 같이 길게 연속적인 패턴에 대해서는 사실적으로 생성해내지 못한다는 문제점 등을 시사하고 있습니다. 연구진은 이러한 문제점에 대해서 모델이 너무 Convolution 연산에 의지한다는 것을 하나의 원인으로 제안합니다. 왜냐하면 convolution 연산은 kernel size에 따라 local한 연산을 반복해서 진행하기 때문에 long-term dependency 측면에서 모델의 사이즈나 optimization 과정에서 정보를 소실한다던가 등의 문제점을 보유하고 있기 때문이라고 합니다. 이러한 문제점에 대한 naive한 해결책으로는 단순히 kernel의 size를 키운다는 방식도 있지만, 이러한 방식은 기존의 CNN이 MLP를 대체할 때 가져왔던 연산량에 대한 이점을 포기한다는 문제점을 갖고 있습니다. 물론 Locality를 잃는다는 문제점도 존재하지만 연산량에 대한 trade-off가 존재하기에 무작정 늘리는 방식은 그닥 좋은 결과를 보이진 않을 것입니다.

이에 대한 해결책으로 연구진이 제안한 것이 Self-Attention mechanism입니다. Feature map에 대해서 Attention mechanism을 접목시킬 시, 멀리 있는 pixel이나 이미지 정보에 대해서도 attention이라는 간단한 연산 하에 서로 dependency를 찾을 수 있을 것입니다. 그렇기에 연구진은 long-term dependency와 computation 사이에서 적절한 balance를 보장해주는 self-attention 기반의 GAN 모델을 제안한 것입니다. 해당 방식은 Generative뿐만 아니라, Discriminator 측면에서도 앞서 말한 기하학적인 패턴과 같은 long-term dependency와 같은 문제를 잘 해결한다고 언급하고 있습니다.

2. Model Structure

SAGAN은 기존의 GAN에 Structure는 유지하지만 feature map들 간에서 일어나는 연산에 대해서 단순히 Convolutional layer를 거치는 것이 아니라 아래와 같은 하나의 Self-Attention Block을 거치는 구조를 가집니다.

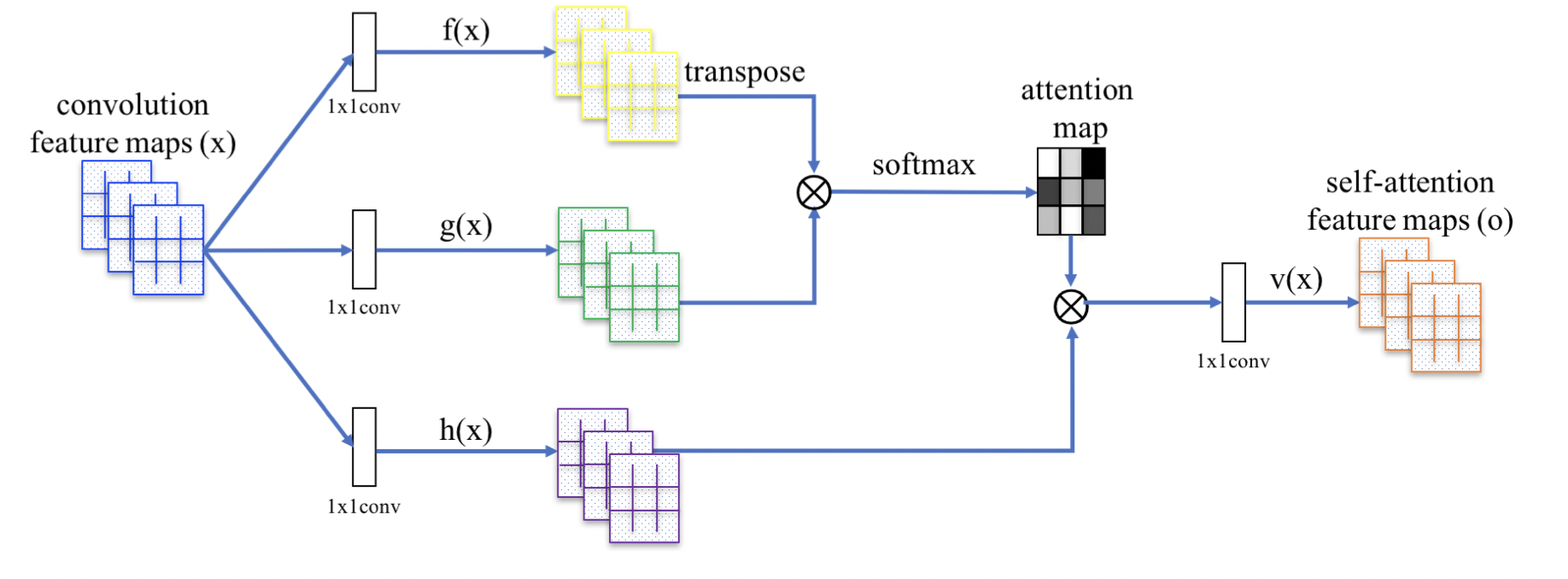
Block에 대해서는 크게 4가지 종류의 weight가 존재한다고 보시면 됩니다. 우선 기존에 Self-Attention 연산은 다음과 같습니다.

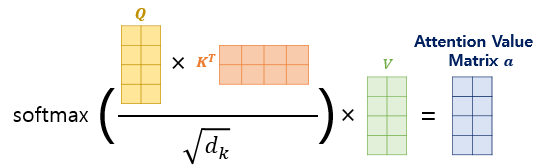
여기서 기존의 Attention에서 Attention Score를 뽑는데 사용되는 Query와 Key의 역할을 하는 $W_f$와 $W_g$가 존재합니다. 식은 다음과 같습니다.

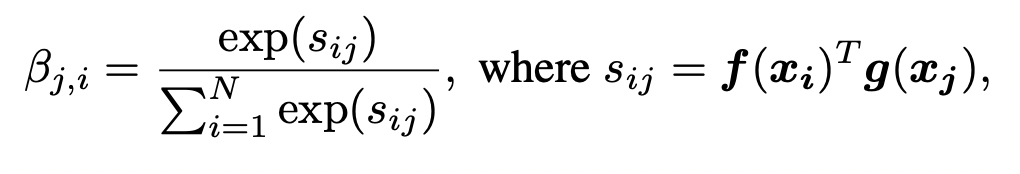
여기서 $f(x_i) = W_fx$ 를, $g(x_j) = W_gx$ 를 의미합니다.
그리고 V의 역할을 하는데 사용되는 $W_h$가 존재합니다. 그리고 차이점이 한가지 있다면 기존의 Attention Value에 대해서 한 번 더 1x1 convolution 연산을 진행해주는 weight인 $W_v$가 존재한다는 것입니다. 이 과정을 식으로 표현하면 다음과 같습니다.

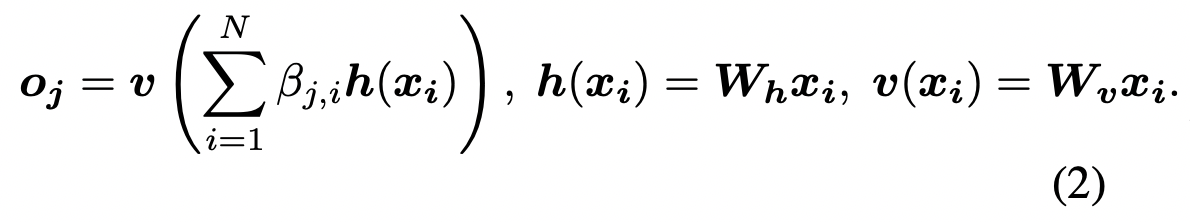
그리고 해당 과정에서 각 Weight들의 차원에 대해서는 연산량을 줄이기 위해 다음과 같이 표현하였습니다. $W_g \in \mathbb{R}^{\bar{C} \times C}$, $W_f \in \mathbb{R}^{\bar{C} \times C}$, $W_h \in \mathbb{R}^{\bar{C} \times C}$, $W_v \in \mathbb{R}^{C \times \bar{C}}$. 여기서 $\bar C$는 연산량을 줄이기 위해 차원을 줄인 값으로 $\bar C = C/k, k = 1,2,4,8$라는 조건을 만족하고 연구진은 computation의 문제로 $k$값을 8로 택했다고 합니다. 그리고 단순히 이러한 output을 사용하기보다는 skip connection 방식을 적용하였고, 최종 결과값은 $y_i = \gamma o_i + x_i$가 된다고 합니다. 이때 $\gamma$값은 학습 가능한 파라미터로 초기값은 0인 상태로 학습된다고 합니다.

Loss Function의 경우에는 기존의 GAN에서 사용하는 adversarial loss와 hinge loss를 사용하였고 아래와 같은 식이라고 합니다.

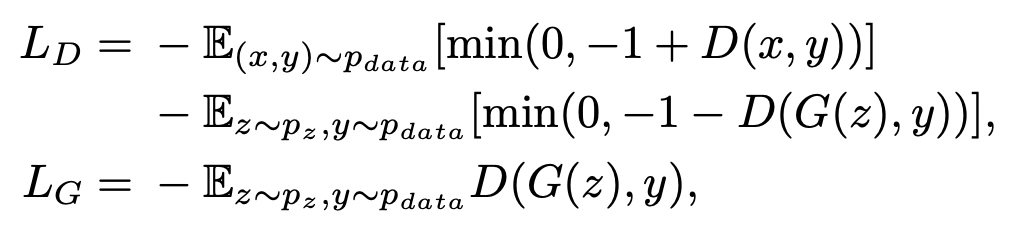
3. Techniques to Stabilize the Training of GANs

GAN의 가장 큰 문제점은 학습이 unstable하다는 것인데요. 연구진은 이를 막기 위해 추가적으로 2가지 기술을 사용했다고 합니다.

3.1. Spectral Normalization

첫 번째로 사용한 기술은 spectral Normalization입니다. 간단하게 설명하면 Weight Normalization의 한 종류로, Weight Matrix에 대해 Spectral Norm을 구한 후 해당 Spectral Norm으로 Weight matrix를 나누어 주는 Normalization 기법입니다.

여기서 Spectral Norm은 어떠한 Weight Matrix를 $W$라고 했을 때, $W$에 대해서 SVD 연산을 시행하고 이때 maximum singlar value을 의미합니다.

해당 방식은 Discriminator $f$에 대해서 Lipschitz constant를 제한하는 방식으로서 학습을 안정화하는 방식으로 알려져 있습니다. 해당 과정에서 Lipschitz constant와 Spectral Norm이 동일하기 때문에 Spectral Norm을 1로 제한함으로써 Lipschitz constant도 제한할 수 있다고 합니다.

3.2. TTUR(Two Time-Scale Update Rule)

두 번째로 사용한 기술은 TTUR입니다. 기존의 GAN들은 Generator와 Discriminator에 대해서 learning rate를 같이 적용했는데 해당 방식은 학습을 진행하는데 있어 낮은 학습속도라는 문제점을 야기했다고 합니다. TTUR은 두 Network에 대해서 따로따로 learning rate를 적용하는 형식으로 Update Rule을 다르게 적용해서 이러한 문제를 해결하는 방법이라고 합니다.

4. Experiment

실험에 앞서 모델 스펙에 대해 설명을 드리면 dataset으로는 Imagenet을 사용하였고, Evaluation Metric으로는 Inception Score와 FID를 사용했다고 합니다. Generator와 Discriminator 모두에서 Self-Attention block은 사용한 형태이며 Adam optimizer을 사용했다고 합니다. TTUR을 적용하는데 있어서 Generator는 learning rate 값을 0.0004로 Discriminator는 0.0001을 사용했다고 합니다. 우선, 3에서 말씀드렸던 기술에 대해서 적용시킨 결과에 대한 비교입니다.

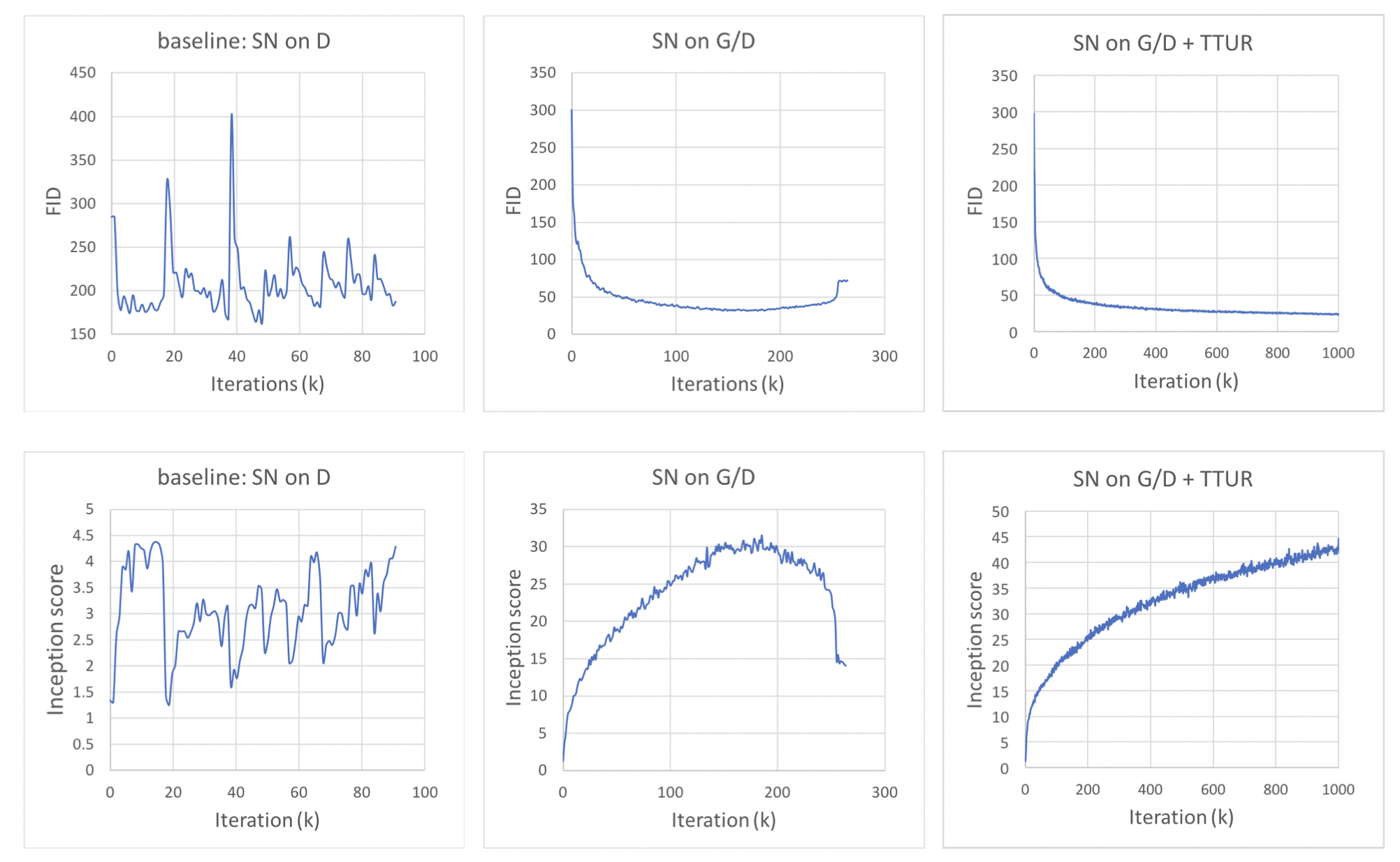
우선 Spectral Normalization을 Discriminator에만 적용시킨 경우에는 학습이 굉장히 불안정함을 확인할 수 있었고, 양쪽에 모두 적용시킨 중간 모델에 대해서는 어느정도 학습이 잘 진행되다가 어느 순간부터 다시 Loss 값이 증가하는 것을 확인할 수 있었습니다. 최종적으로 모든 기술을 적용시킨 마지막 모델은 Iteration이 증가할수록 loss값이 잘 줄어드는 것을 볼 수 있습니다.

다음 실험은 각 모델에서 사용하는 Feature map의 size에 따른 성능 비교입니다. baseline으로는 resnet backbone의 GAN을 사용하였고 결과는 다음과 같습니다.

여기서 $feat_k$는 $k \times k$ size의 feature map을 의미합니다. resnet base의 model의 경우에는 작은 size의 feature map에 대해서 더 좋은 성능을 보이는 반면 SAGAN의 경우에는 feature map의 size가 클수록 더 좋은 성능을 보이는 경향을 띄고 있습니다. 이에 대해서 연구진은 larger feature map에 대해서 attention 연산이 택할 수 있는 evidence나 어느 feature에 더 attention을 할 수 있는지에 대한 자유도가 높기 때문이라고 설명하고 있습니다. 그리고 제일 좋은 성능을 내는 모델에 대해서 비교를 해봤을 때, SAGAN이 더 좋은 결과를 내는 것도 역시 확인할 수 있습니다. 아래는 당시 SOTA 모델들과 비교했을 때, SAGAN의 결과입니다.

마지막으로 기존의 SOTA인 SNGAN-projection과의 결과 비교에 대해서 설명드리고 마무리하려 합니다. 아래 이미지에서 첫 라벨의 좌측에 있는 숫자가 SAGAN의 FID값이고 우측에 있는 숫자가 SN-GAN의 FID입니다. 연구진이 Introduction에서 말했듯이 SAGAN은 복잡하고 반복되는 long-term dependency의 정보를 갖고 있는 이미지에 대해서 강점을 갖고 있습니다. 그렇기에 모든 종류의 이미지에 대해서 더 좋은 성능을 보이는 것이 아니라 복잡한 패턴을 지닌 강아지의 털, 물고기의 비늘 등을 보유한 이미지에 대해서 더 좋은 성능을 보이고 상대적으로 단순한 패턴을 보유하고 있는 돌담이나 풍경 이미지에 대해서는 SNGAN이 성능이 더 좋은 것을 확인할 수 있습니다.