아직 학생이기도하고 영어가 미숙하다보니 본 리뷰에 오류가 있을 수도 있습니다. 이 점 감안해주시고 혹시나 찾으신다면 피드백 감사히 받겠습니다.

Introduction

3D Information에 대해서 표현하는 다양한 방식 중, NeRF는 5D input$(x,y,z,\theta,\phi)$를 기반으로 viewpoint에 대한 색상값을 return하고 이를 volume rendering을 활용해 이미지를 생성해내는 방식으로 현재 좋은 결과를 보여주고 있습니다. 하지만 이런 NeRF에 대해서 dataset 부분에서 어느정도 제한점이 있는데요. NeRF가 좋은 성능을 보여줄 수 있음은 정적인 image를 사용했기 때문이라고 합니다. 즉, 동일 시점에 대해서 다양한 각도의 카메라에서 동시 촬영을 진행해야한다는 것이죠. 하지만 현실 세계에서의 dataset을 생성하기 위해서는 이러한 점이 보존되지 않습니다. 하나의 카메라로 여러 각도에서 찍는 방법이 있겠지만 아무리 가만히 있으려고 해도 피사체에 대해서 어느정도 움직임은 생길 수 밖에 없고, 바람, 주변 환경, 광원 등에 대한 사진에 끼치는 미세한 변화등 역시 피할 수 없습니다. 그렇기에 Nerfies는 이렇게 보존되지 못하고 어느정도 변형되는 정보들에 대한 $(x,y,z)$값들을 deformation field를 거쳐 하나의 canonical field로 옮겨준 후 연산을 진행해 이러한 문제들을 어느정도 해결할 수 있게 합니다.

Method

NeRF

우선 Nerfies를 이해하기 위해서는 NeRF에 대한 이해가 수반되어야 합니다. 이를 위해서는 제 블로그의 조회수 효자 글인 다음 글이 조금 도움이 될 것 같습니다.

https://velog.io/@mer9ury/NeRF-Representing-Scenes-as-Neural-Radiance-Fields-for-View-Synthesis-Review

그래도 간단하게 설명을 드리자면, 특정 viewpoint로부터 한 픽셀에 대해서 ray를 casting해서 이미지를 생성합니다. 그리고 각 pixel은 ray와 object가 맞닿는 3D viewpoint의 $R,G,B$(color)와 $\sigma$(density)들을 종합해서 구성됩니다. 그리고 $(x,y,z,\theta,\phi) \rightarrow (R,G,B,\sigma)$을 구현하는 함수를 바로 MLP Layer로 구현한 모델이 NeRF입니다. 그리고 이 과정에서 high-frequency data를 위한 positional encoding과 Hierarchical Modeling등 다양한 기법이 존재하는데 해당 내용에 대해서는 위의 글 참조하시면 좋을 것 같습니다.

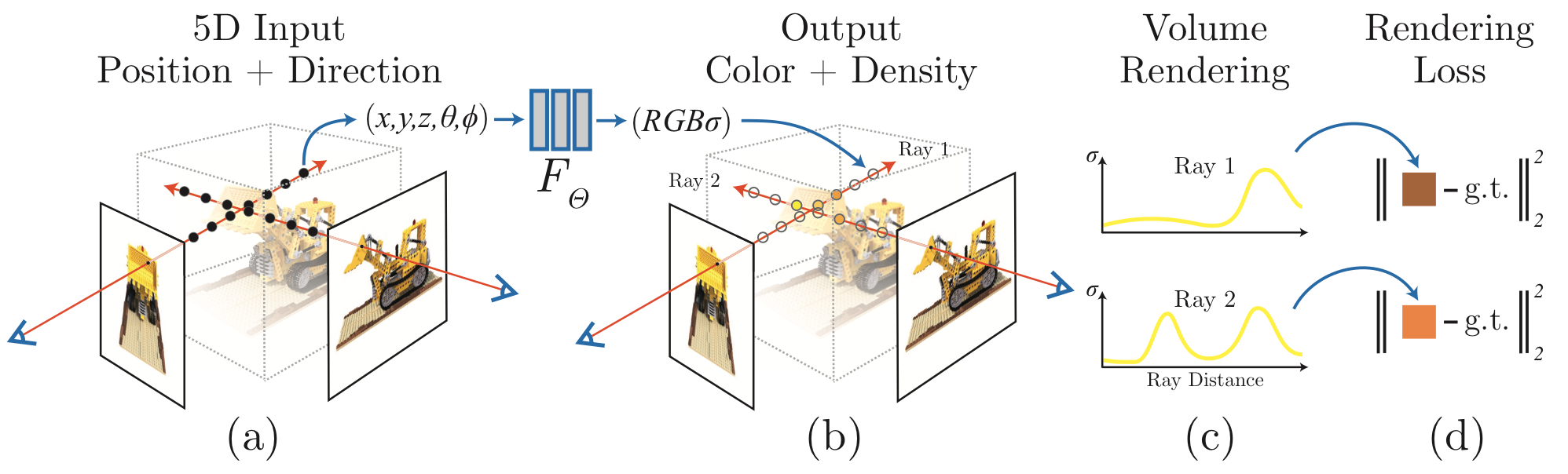
NeRF with deformation

하지만 이러한 NeRF는 다음과 같은 한계가 있습니다. 위에서도 언급되었듯 object가 static해야만 한다는 단점이죠.그래서 Nerfies는 ray를 직접적으로 casting하는 것이 아니라 이를 canonical space로 옮기고 sampling을 진행했습니다. 정적인 여러 카메라의 데이터가 아닌 영상 데이터에서 각 frame마다의 learnd latent deformation code $w_i$를 두고 해당 값을 기반으로 casting하고자 하는 3d 좌표값 $\textbf x$을 Canonical space($\textbf{x}^\prime$)로 옮겨줍니다. 즉 $T_i: \textbf {x} \rightarrow \textbf{x}^\prime$라는 deformation 연산을 정의하고 $T_i$를 정의 해주는 parameter는 $T:(\textbf x,w_i) \rightarrow \textbf{x}^\prime$로 정의해주는 것입니다. 즉, 식은 아래와 같이 정리될 수 있습니다.

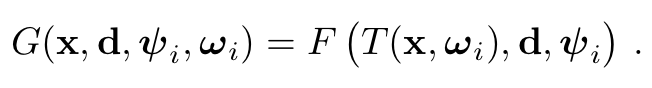
이때 쓰인 $\psi_i$는 NeRF-W에서 쓰인 parameter입니다. 여기서 NeRF-W란 NeRF와 같이 제한된 환경 속에서의 실험이 온라인에 많은 dataset을 보유하고 있는 landmark에 대해 사진의 조건마다 appearance를 드러내주는 latent code $\psi_i$를 두고, 이를 기반으로 어느정도 conditional하지만 static한 object에 대해서는 consistency를 갖춘 NeRF모델을 말합니다. Nerfies에서도 각 frame마다의 exposure, white balance등의 요소들을 어느정도 조절할 수 있게 이와 같은 NeRF-W에서의 개념을 사용한다고 합니다.

그렇다면 여기서 deformation 과정은 어떻게 작동할까요? naive하게 설명할 경우, 위에서 말했던 T 자체를 MLP로 해결합니다. $\textbf x$와 $w_i$를 input으로 받아 최종적으로는 $\textbf{x}^\prime$을 output으로 뱉는 모델을 설계합니다. 하지만 단순히 이렇게 옮기기보다는 rotation parameter와 translation parameter을 활용해서 deformation을 구현해준다고 합니다. 다만 그 과정에서 $W:(\textbf x,w_i) \rightarrow \textbf {SE}(3)$의 형식으로 정의를 하는데 여기서 screw axis를 사용해 다음과 같이 rotation과 translation을 정의한다고 합니다.


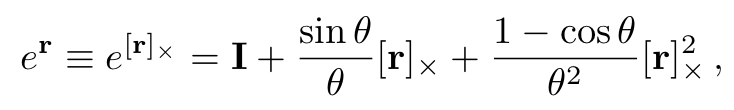
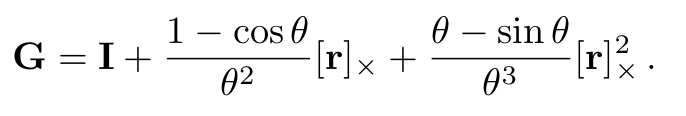
추가적인 equation에 대해서 설명을 드리면 $\textbf r$에 대해서는 lie algebra를 기반으로 설계했다고 해 $e^\textbf r \in \textbf{SO}(3)$에 속한다고 합니다. 최종 식은 다음과 같다고 볼 수 있습니다.

$\textbf{x}^\prime = e^\mathcal S \textbf x = e^\textbf r \textbf x + \textbf p$, where $\textbf{p=Gv}$ and $\mathcal S = (\textbf r;\textbf v) \in \mathbb R^3$

사실 이 부분에 대해서 완벽한 수학적인 이해는 하지 못했습니다. screw axis에 대해서 여러 조사도 해봤는데 아직 수학적 능력과 구글링 능력의 부족으로 인해서... 뒤에 이어지는 elastic energy에 대한 개념도 잘은 모르지만 일단 적혀있는 대로 열심히 풀어보겠습니다.

Elastic Energy

deformation field는 상당한 ambiguity를 보유하고 있고 이를 elastic energy 제한을 통해서 어느정도 해결할 수 있다고 합니다. 우선 수식적으로 deformation field T의 경우 $w_i$가 고정되어 있다고 하더라도 들어오는 $\textbf x$값에 따라 transformation matrix 자체가 변경되기에 non-linear mapping이라고 할 수 있습니다. 하지만 그 순간순간에 matrix에 대해서는 linear하게 구할 수 있고 이를 the best linear approximation of the transofrmation at that point라고 볼 수 있습니다. 그리고 이 Transformation의 Jacobian에 대해서 SVD를 하고 이를 기반으로 closest Rotation을 빼준 값의 Frobenius norm을 제한하는 방식으로 ambiguity 문제를 해결할 수 있다고 합니다. 즉 식은 다음과 같이 풀어쓸 수 있는데요. $\textbf J_T = \textbf U\Sigma \textbf V^T$에서

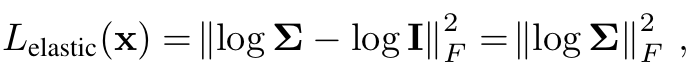
그리고 추가적으로 더 robust한 loss를 제공하기 위해 아래와 같이 식을 변형했다고 합니다.

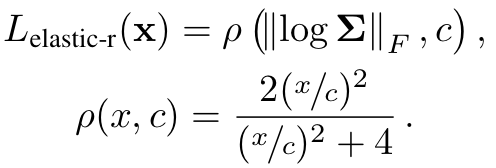
Background Regularization

deformation에 대한 setting이 너무 자유롭다면 deformation field가 가만히 있는 배경에 대한 정보까지도 변형할 수도 있습니다. 그렇기에 앞서 background와 object에 대해서 parsing을 1차적으로 진행하고 background 부분에 해당하는 3D point들에 대해서는 아래와 같은 loss를 적용해 Background는 최대한 deformation이 일어나지 않도록 설정했다고 합니다.

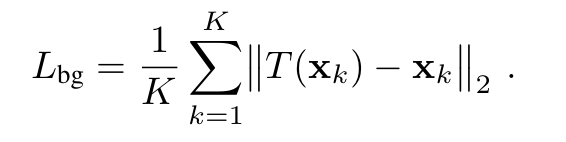
Coarse-to-Fine Deformation Regularization

NeRF에서 사용하는 positional encoding을 분석하는 논문을 보면 encoding하는 $sin$과 $cos$을 설정하는 값이 클수록, 즉 주파수가 높을수록 image의 high-frequency에 대한 정보를 잘 보존(small expression)하고 반대로 낮을수록 low-frequency에 대한 정보(head rotation)를 잘 보존한다고 합니다. 아래는 이를 보여주는 frequency($m$)에 따른 실험결과입니다.

그래서 연구진은 단 하나의 positional encoding 값을 사용하는 것이 아니라 아래 식을 통해 처음에는 low-frequency 위주로 학습을 하다가 high-frequency로 넘어가는 형식으로 조절을 해가며 사용했습니다.
$\gamma_\alpha(\textbf x) = (\textbf x, \cdots, w_k(\alpha)sin(2^k\pi\textbf x), w_k(\alpha)coss(2^k\pi\textbf x), \cdots)$, where $\alpha(t) = {mt \over N}, t=$ # of iteration

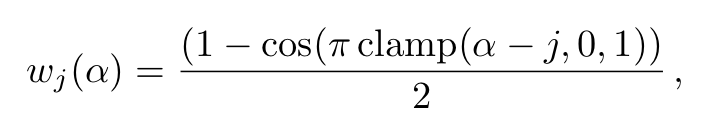
Experiment

Nerfies는 MLP model의 경우에는 NeRF와 유사하게 사용하였고 다만 activation function을 Softplus로 변경했다고 합니다. 추가적으로 사용되는 deformation network에 대해서는 depth 6, hidden size 128에 4번째 layer에서 skip connection이 사용되는 구조를 취했다고 하고, 256 coarse and fine ray sampling을 진행했다고 합니다. 위에서 언급한 Coarse-to-Fine optimization을 위해 $\alpha$는 0~6까지 80K 번의 Iteration을 통해 linearly하게 증가시켰다고 합니다. 최종 Loss는

$L_{total} = L_{rgb} + \lambda L_{elastic-r} + \mu L_{bg}$로 $\lambda = \mu = 10^{-3}$이라고 합니다.
Dataset의 경우에는 직접 촬영한 영상을 사용한 것 같습니다.
실험결과는 다음과 같습니다.

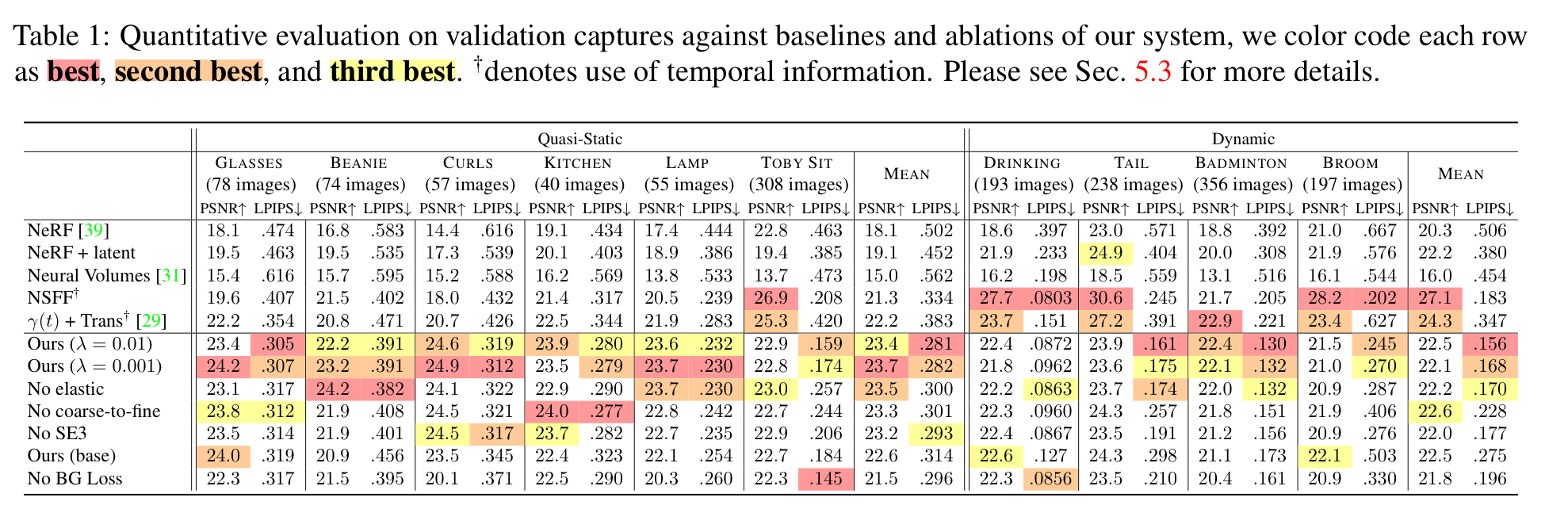
우선 static한 data들에 대해서는 Nerfies가 더 좋은 성능을 보여주는 것을 확인할 수 있고 Dynamic한 이미지에 대해서는 NSFF가 제일 좋은 성능을 보여주지만 LPIPS 측면에 대해서는 Nerfies가 더 좋은 성능을 보여주는 것을 확인할 수 있습니다.

아래는 실험결과에 대한 이미지입니다.

Deformation field라는 개념을 3D 공부하면서 심심치않게 봤는데 이번 논문으로 어느정도 가닥이 잡힌 느낌입니다. 하지만 아직 좌표계와 선형대수의 늪에서 헤어나오지는 못한 느낌이라 아쉽네요. 다음 논문은 아마도 Nerfies의 후속작인 HyperNeRF가 될 것 같습니다. 위에 실험결과에서 Dynamic한 Image에 대해서 조금 아쉬운 점이 있었지만 이에 대해서 Level method로 해결한 논문인데 그건 Nerfies보다는 쉽게 읽혀서 금방금방 쓸 것 같습니다...

그러면 이제 취미?인 개발을 하러...