크리스마스 "트리"?

시작하며
오늘은 자료구조 중 하나인 트리(Tree) 에 대해 알아보겠습니다.
트리 너 뭥미
트리는 노드(Node)들이 마치 나무 가지처럼 계층적으로 연결되어 있는 비선형 자료구조입니다.
비선형 자료구조?
비선형 자료구조란 데이터를 순서대로 나열하지 않고, 서로의 관계를 통해 구조적으로 표현하는 방식을 말합니다.
예를 들어 트리와 그래프가 있습니다.
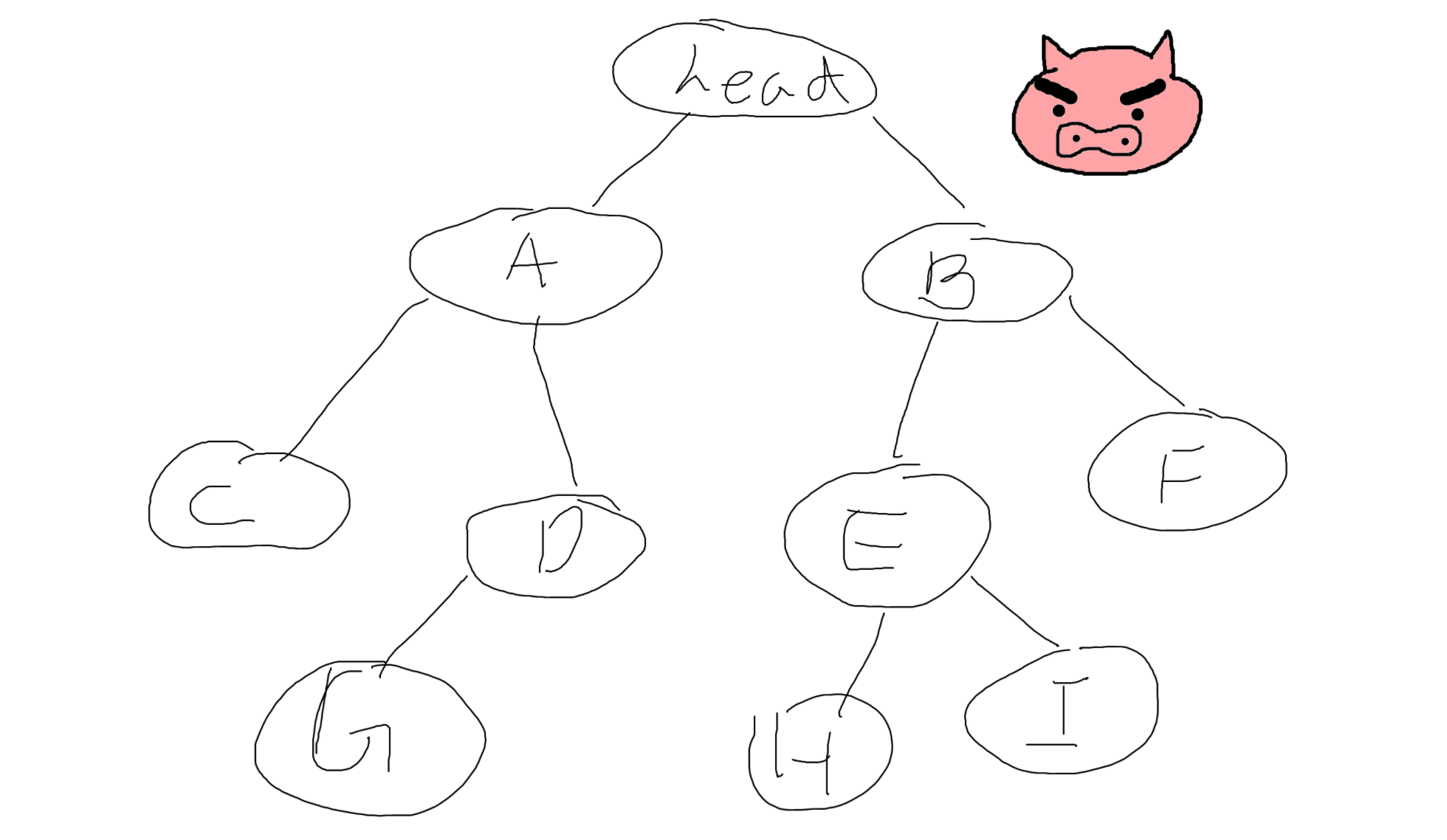
이런식으로 생겼습니다.
선형 자료구조?
그렇다면 선형 자료구조란 무엇일까요?
선형 자료구조란 데이터가 한 줄로 차례차례 정렬되어있는 구조 입니다
각 데이터 요소는 바로 이전 요소와 바로 다음 요소와만 직접적으로 관계를 가집니다.
예를 들어 배열, 연결리스트, 스택, 큐와 같은 것 들이 있습니다.
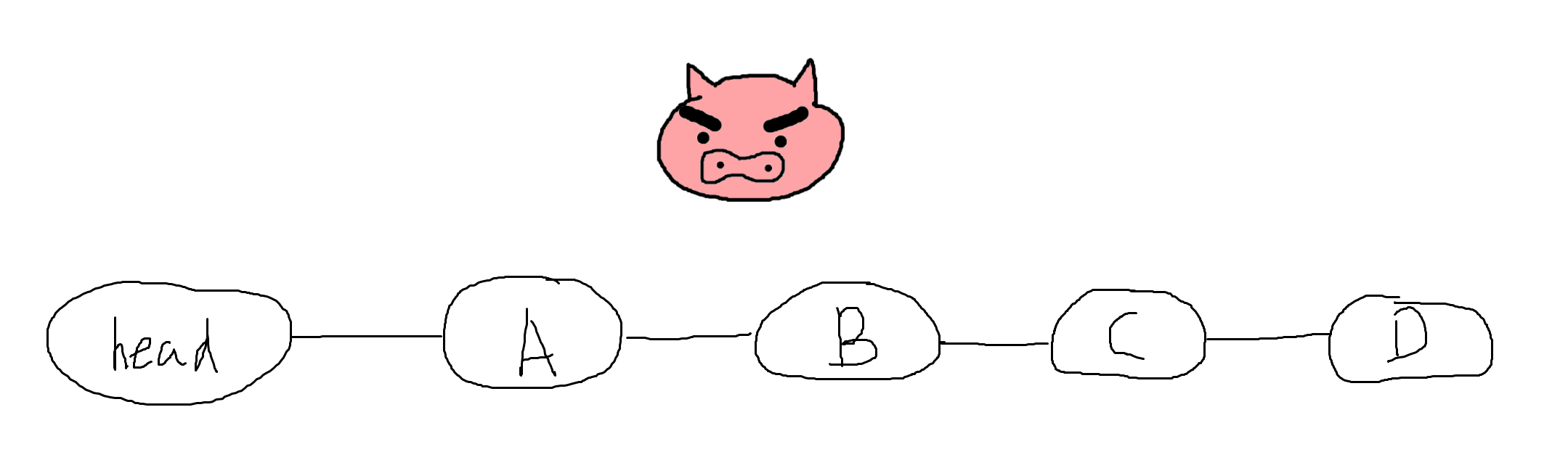
이런 식으로 생겼습니다.
트리의 기본 용어
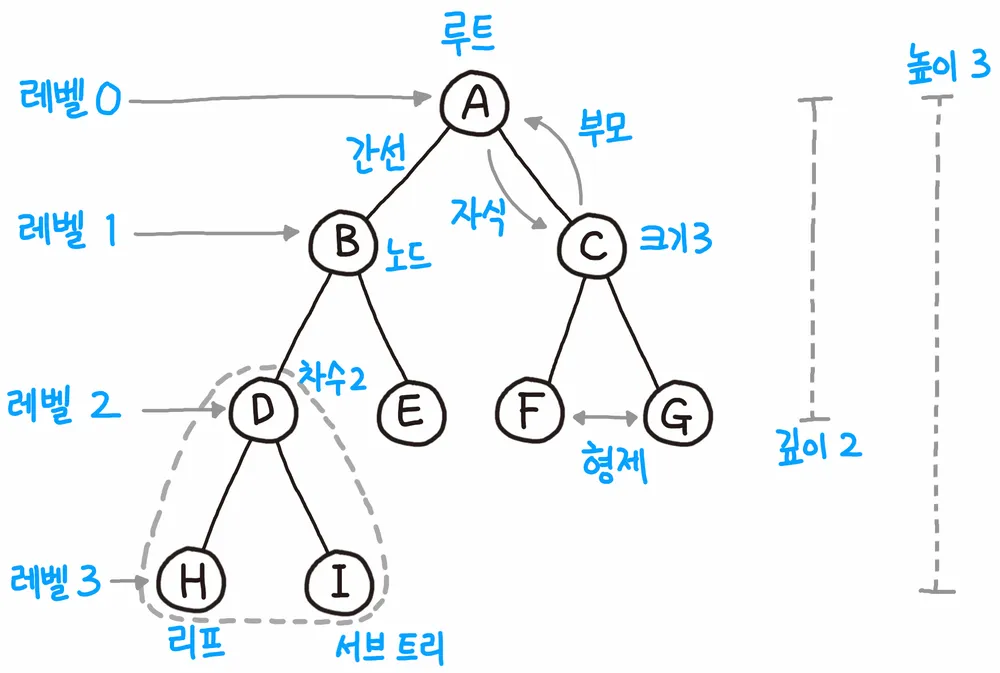
- 루트(root)
트리의 맨 꼭대기, 최상위노드
예) 저 사진의 트리의 루트는 A - 노드(node)
트리의 기본 단위(데이터) - 단말 노드
자식이 없는 노드(차수가 0인 노드) - 비단말 노드
적어도 하나의 자식을 갖는 노드 - 간선
노들들을 잇는 선 - 서브트리
하나의 노드와 그 노드들의 자손들로 이루어져있는 것 - 차수
노드가 가지고 있는 자식 노드이 개수
예) D의 차수는 2 - 레벨
각층의 번호
예) B의 레벨은 1 - 높이
어떤 노드부터 가장 깊은 리프 노드까지 경로 길이
예) 저 사진에 나와있는 트리의 높이는 3
이진 트리
이진 트리는 단말노드를 제외한 각 노드의 차수가 2개인 것
특징으로는 구현이 편하고 서브트리간 순서가 존재 합니다.
-> 왼쪽 자식노드 오른쪽 자식노드
그래서 같은 루트에 같은 자식노드 하나를 가지고 있어도 자식노드의 위치가 각각 왼쪽과 오른쪽으로 다르다면 그 두 트리는 서로 다른 트리가 됩니다.
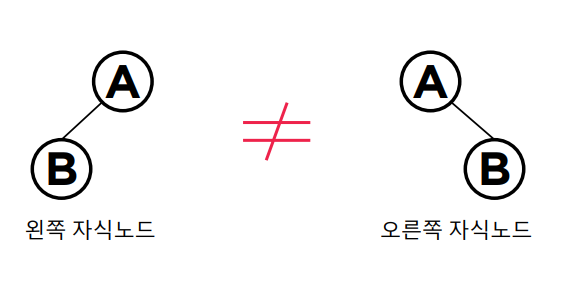
최대 2개이기 때문에 자식이 1개 있을 수도 있고, 없을 수도 있습니다.
이진 트리의 장점
차수가 2개라 구현이 편하다
서브트리간 순서가 존재
포화 이진 트리
노드가 더이상 들어가지 않는 이진트리의 포화상태 입니다.
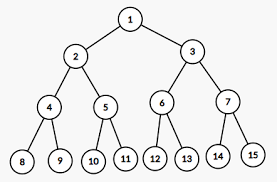
완전 이진 트리
왼쪽부터 값이 차례대로 노드에 값이 차있는 상태입니다.
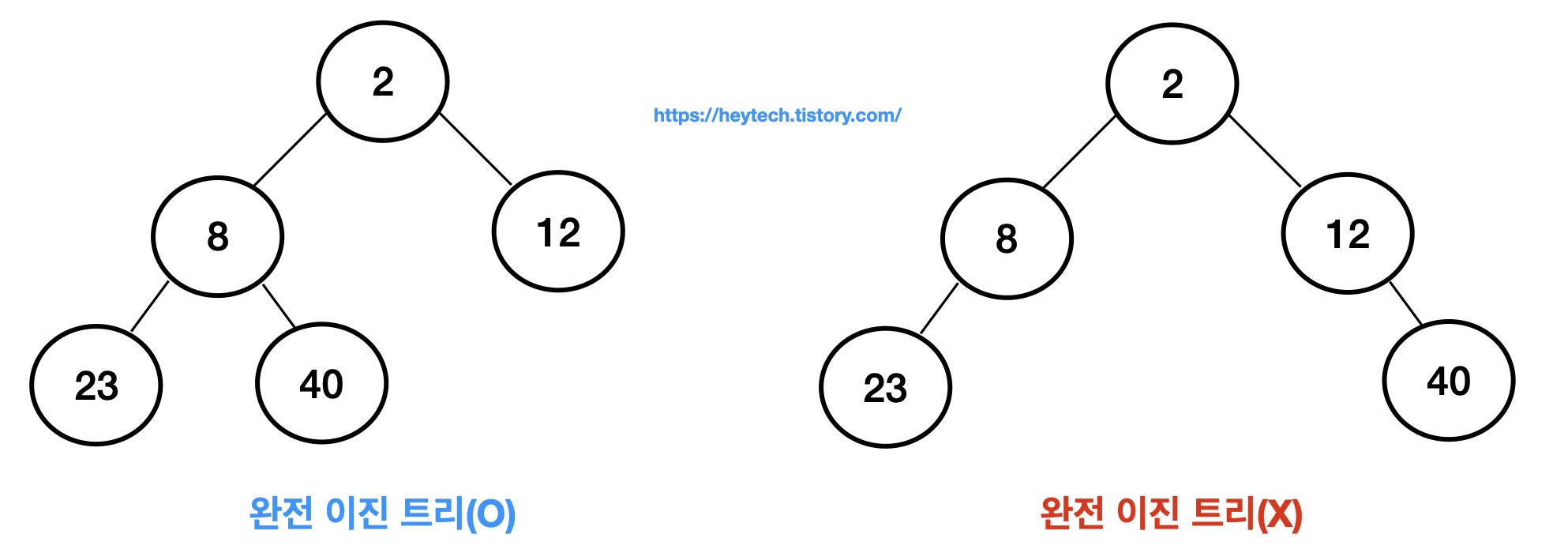
간선 개수 구하기
노그의 개수가 n이면 간선의 개수 n-1
루트는 부모로 가는 간선이 없음 따라서 간선의 개수는 n-1
노드 개수 구하기
높이가 h인 이진트리 경우 최소 h의 노드를 가짐
최대 2^h-1개의 노드를 가짐
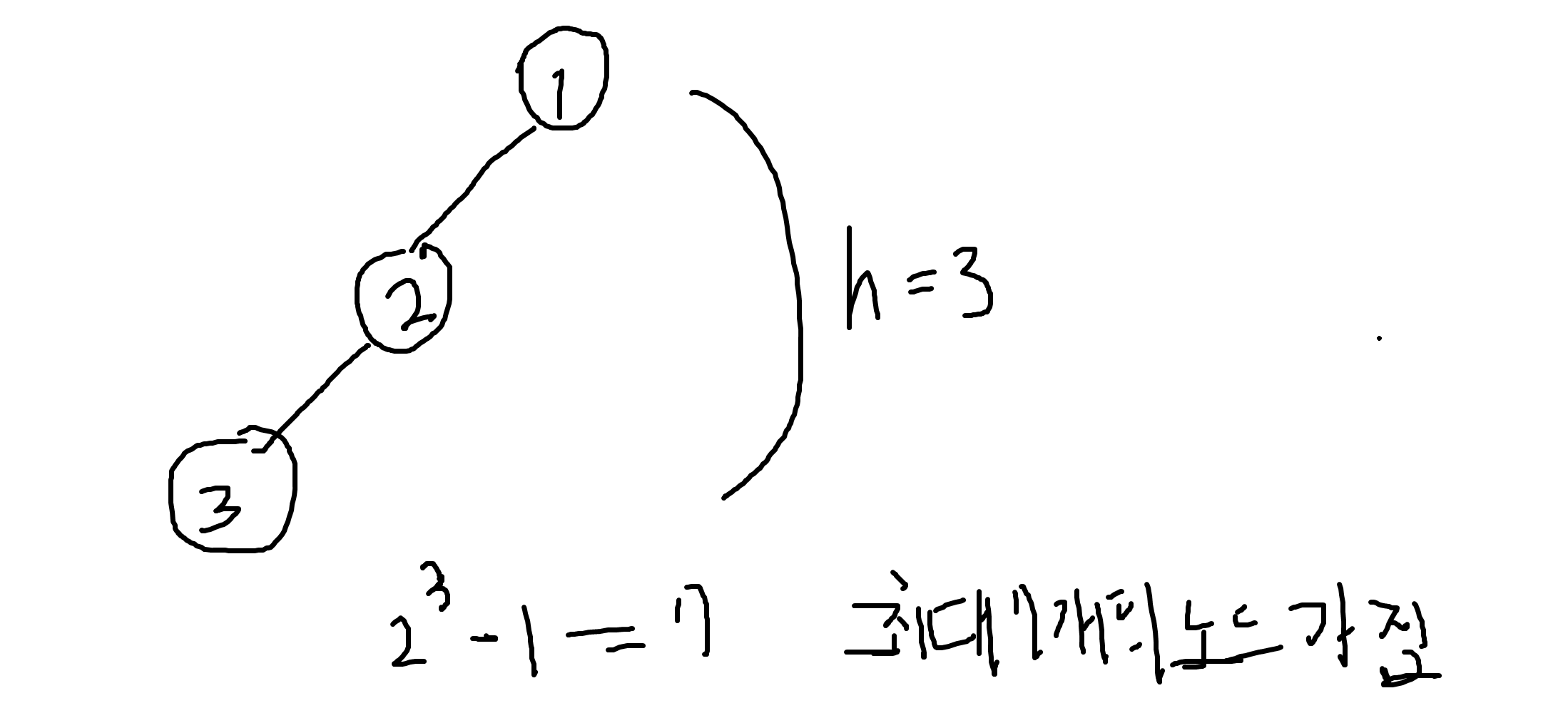
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def count_nodes(root):
if root is None:
return 0
return 1 + count_nodes(root.left) + count_nodes(root.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
print(count_nodes(root))
- Node 클래스: 트리의 기본 구조
- count_nodes() 함수: 재귀로 왼쪽 + 오른쪽 + 현재 노드 수를 합함
이진 탐색 트리 (Binary Search Tree, BST)
정의
이진 탐색 트리(BST)는 왼쪽 서브트리에는 작은 값, 오른쪽 서브트리에는 큰 값이 저장되는 이진 트리(Binary Tree) 구조입니다.
이 규칙을 이용하면 탐색, 삽입, 삭제 연산을 효율적으로 수행할 수 있습니다.
주요 연산
삽입 (Insert)
이진 탐색 트리는 왼쪽 < 루트 < 오른쪽 규칙을 유지해야 합니다.
따라서 새 값을 넣을 때, 현재 노드 값과 비교하면서
왼쪽 또는 오른쪽으로 이동하며 삽입한다.
def insert(tree, i, key):
while len(tree) <= i:
tree.append(None)
if tree[i] is None:
tree[i] = key
elif key < tree[i]:
insert(tree, 2*i+1, key) # 왼쪽으로 이동
elif key > tree[i]:
insert(tree, 2*i+2, key) # 오른쪽으로 이동
삭제 (Delete)
노드를 삭제할 때는 세 가지 경우를 고려해야 합니다:
- 단말노드인 경우
그냥 삭제 - 자식이 하나인 경우
부모랑 자식이랑 이어줌 - 자식이 둘인 경우
오른쪽 서브트리의 가장 작은 값 즉 자신 바로 다음으로 큰 값으로 대체
하지만 배열 기반 트리에서는
링크를 직접 이어주는 게 어렵기 때문에,
단순히 해당 값 위치를 None으로 바꾸는 방식으로 구현하였습니다.
def delete(tree, i, key):
if i >= len(tree) or tree[i] is None:
return
if tree[i] == key:
tree[i] = None
elif key < tree[i]:
delete(tree, 2*i+1, key)
else:
delete(tree, 2*i+2, key)
실행 코드
def insert(tree, i, key):
while len(tree) <= i:
tree.append(None)
if tree[i] is None:
tree[i] = key
elif key < tree[i]:
insert(tree, 2*i+1, key)
elif key > tree[i]:
insert(tree, 2*i+2, key)
def delete(tree, i, key):
if i >= len(tree) or tree[i] is None:
return
if tree[i] == key:
tree[i] = None
elif key < tree[i]:
delete(tree, 2*i+1, key)
else:
delete(tree, 2*i+2, key)
# 실행
t = []
for x in [50, 30, 70, 20, 40, 60, 80]:
insert(t, 0, x)
print("삽입 후:", t)
delete(t, 0, 70)
print("삭제 후:", t)
트리의 순회
트리의 모든 노드를 일정한 규칙에 따라 방문하는 과정을 “순회”라고 합니다.
크게 전위, 중위, 후위, 레벨 순회가 있습니다.
전위 순회 (VLR)
루트 → 왼쪽 → 오른쪽
트리 구조를 복사하거나 표현할 때 유용합니다.
def preorder(i):
if i >= len(tree) or tree[i] is None:
return
print(f"[{tree[i]}]", end=' ')
preorder(2*i + 1)
preorder(2*i + 2)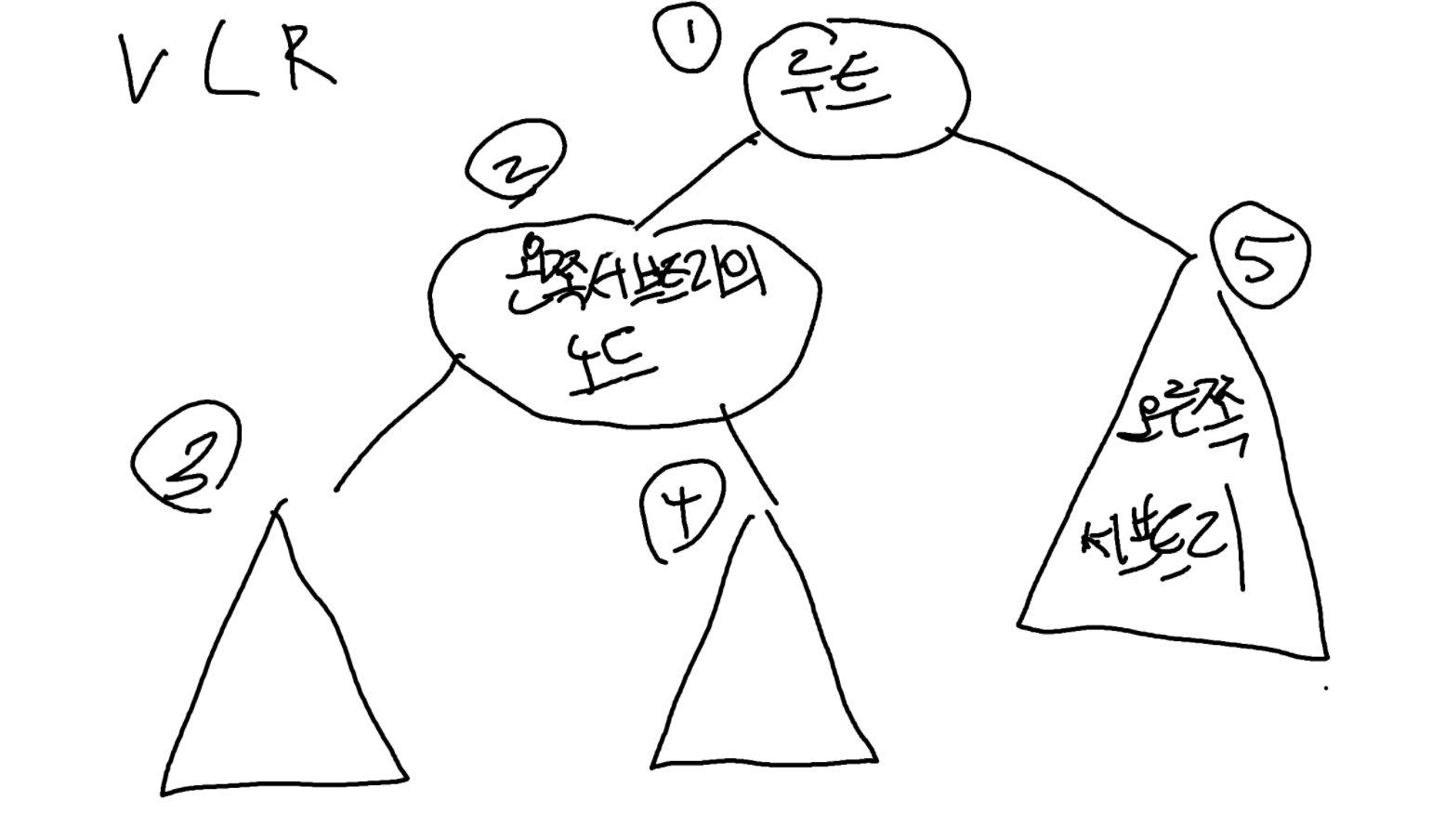
중위 순회 (LVR)
왼쪽 → 루트 → 오른쪽
이진 탐색 트리에서 오름차순 정렬된 결과를 얻을 수 있습니다.
def inorder(i):
if i >= len(tree) or tree[i] is None:
return
inorder(2*i + 1)
print(f"[{tree[i]}]", end=' ')
inorder(2*i + 2)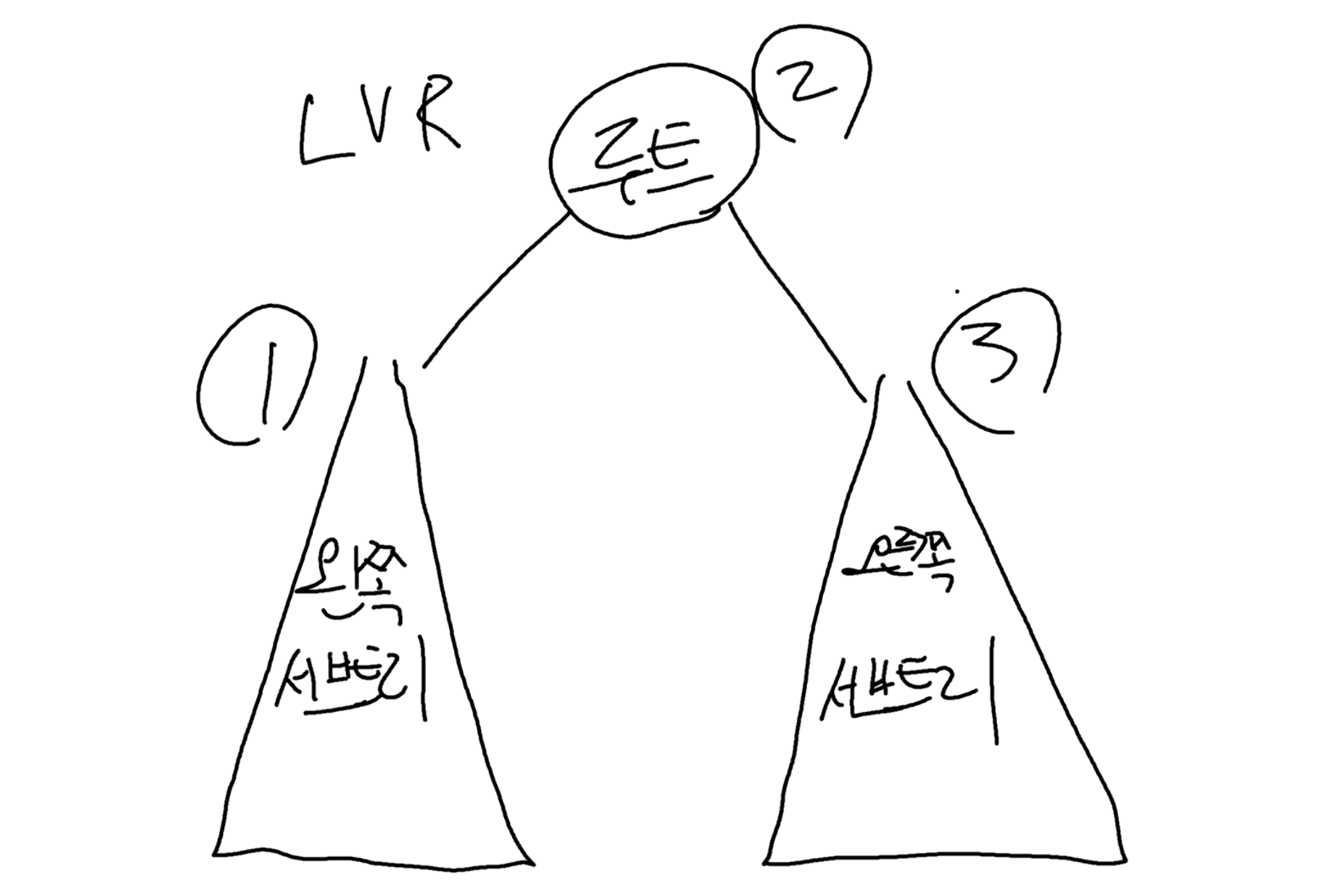
후위 순회 (LRV)
왼쪽 → 오른쪽 → 루트
트리를 삭제하거나 메모리 해제할 때 주로 사용됩니다.
def postorder(i):
if i >= len(tree) or tree[i] is None:
return
postorder(2*i + 1)
postorder(2*i + 2)
print(f"[{tree[i]}]", end=' ')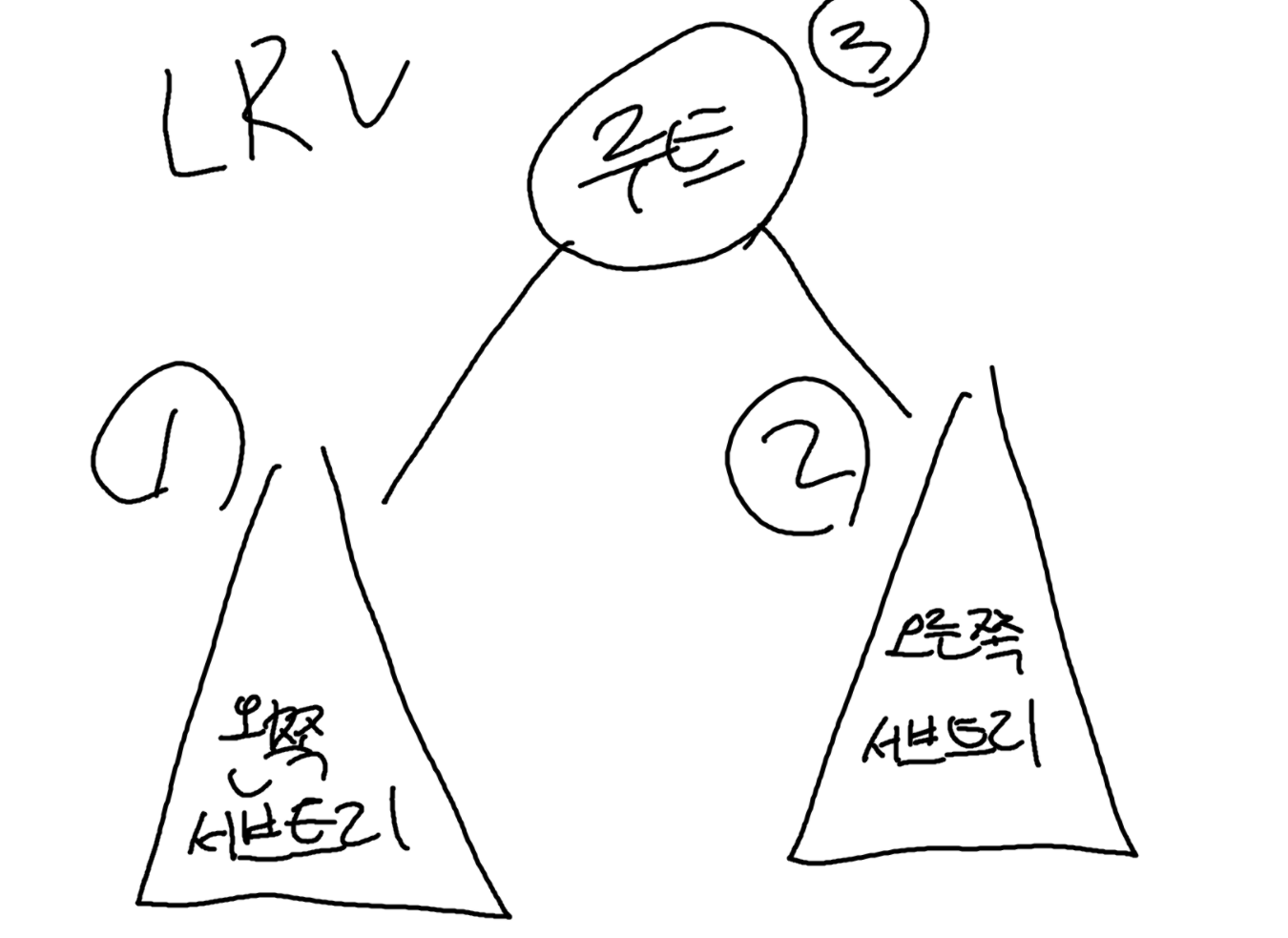
# 트리를 배열로 표현
tree = [1, 2, 3, 4, 5, None, 6]
# 전위 순회
def preorder(i):
if i >= len(tree) or tree[i] is None:
return
print(f"[{tree[i]}]", end=' ')
preorder(2*i + 1)
preorder(2*i + 2)
# 중위 순회
def inorder(i):
if i >= len(tree) or tree[i] is None:
return
inorder(2*i + 1)
print(f"[{tree[i]}]", end=' ')
inorder(2*i + 2)
# 후위 순회
def postorder(i):
if i >= len(tree) or tree[i] is None:
return
postorder(2*i + 1)
postorder(2*i + 2)
print(f"[{tree[i]}]", end=' ')
# 실행
print("preorder : ", end='')
preorder(0)
print("\ninorder : ", end='')
inorder(0)
print("\npostorder: ", end='')
postorder(0)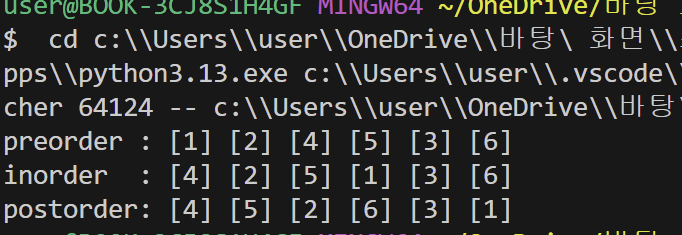
레벨 순회 (Level-order Traversal)
레벨 순회는 각 노드를 레벨순으로 검사하는 순회 방법입니다. 루트 노드의 레벨이 1이고 아래로 내려갈수록 레벨은 증가합니다. 동일한 레벨의 경우 왼쪽에서 오른쪽으로 방문합니다.
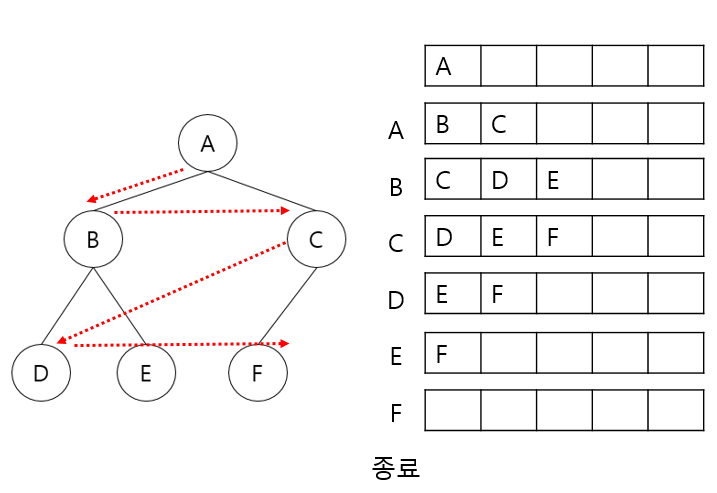
레벨 순회 코드는 큐에 하나라도 노드가 있으면 계속 반복하는 코드로 이루어져 있습니다. 먼저 큐에 있는 노드를 꺼내어 방문한 다음 그 노드의 자식 노드를 큐에 삽입하는 것으로 한번의 반복을 끝냅니다. 이러한 반복을 큐에 더 이상의 노드가 없을 때까지 계속합니다.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def level(root):
if root is None:
return
q = [root]
while q:
n = q.pop(0)
print(n.data, end=' ')
if n.left:
q.append(n.left)
if n.right:
q.append(n.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
level(root)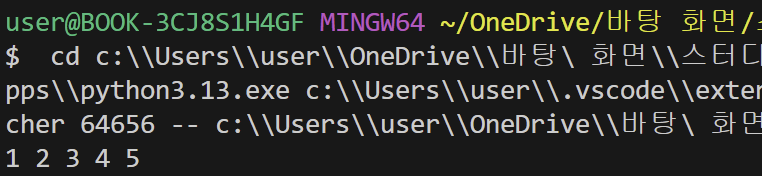
- 배열 q[]를 큐처럼 사용
- 루트부터 꺼내서 출력하고
- 왼쪽→오른쪽 자식을 차례로 넣음
