그래프
그래프란?
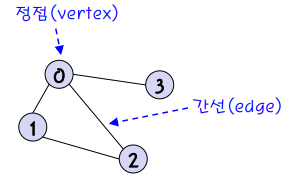
그래프는 정점(Vertex) 과 간선(Edge) 의 집합으로 표현됩니다.
- 정점
여러가지 특성을 가질 수 있는 객체(식별이 가능한 특성)
노드라고도 불림 - 간선
정점들 사이의 관계
링크라고도 불림
예를 들어,
V(G1) = {0, 1, 2, 3}
E(G1) = {(0,1), (0,2), (0,3), (1,2)}이렇게 표현할 수 있습니다.
여기서 V(G)는 정점들의 집합, E(G)는 간선들의 집합을 의미합니다.
무방향 그래프 vs 방향 그래프
그래프는 간선의 방향성 유무에 따라 두 가지로 나뉩니다.
무방향 그래프
- 간선에 방향이 없는 그래프
- A—B가 있다면 B—A도 자동으로 연결된 상태입니다.
- 친구 관계, 도로 지도 등 양방향 관계를 표현할 때 사용
특징
- A에서 B로 갈 수 있으면 B에서 A로도 가능
- 간선 수는 중복 없이 한 번만 기록 (예: A-B 한 줄)
방향 그래프 (Directed Graph)
- 간선에 방향이 있는 그래프
- A → B는 가능하지만, B → A는 아닐 수도 있습니다.
- 인스타그램 팔로우, 웹페이지 링크 등 일방향 관계를 표현할 때 사용
특징
- 간선이 방향성을 가지므로, 연결 구조가 복잡할 수 있음
- 사이클(순환)이 생기면 특정 정점으로 되돌아오는 경우도 존재

네트워크(Weighted Graph)
각 간선에 가중치(weight) 가 부여된 그래프를 네트워크 또는 가중치 그래프라고 합니다.
예를 들어 도로의 거리, 통신 비용, 연결 속도 등을 표현할 때 사용됩니다.
정점의 차수 (Degree)
그래프에서 인접 정점은 간선으로 직접 연결된 정점을 말합니다.
무방향 그래프에서 정점의 차수 는 인접한 정점의 수입니다.
모든 정점의 차수를 합하면 간선 수의 두 배가 됩니다.
방향 그래프에서는 들어오는 간선의 수를 진입 차수,
나가는 간선의 수를 진출 차수 라고 합니다.
경로와 사이클
- 경로(Path): 한 정점에서 다른 정점으로 이동하는 순서의 나열
- 단순 경로(Simple Path): 같은 간선을 반복하지 않는 경로
- 사이클(Cycle): 시작과 끝이 같은 단순 경로
연결 그래프와 완전 그래프
- 연결 그래프: 모든 정점 쌍 사이에 경로가 존재하는 그래프
- 비연결 그래프: 일부 정점이 다른 정점과 연결되어 있지 않은 그래프
- 완전 그래프: 모든 정점이 서로 직접 연결된 그래프
정점이 n개일 때 간선의 개수 = n × (n - 1) / 2
그래프의 표현 방식
인접 행렬
인접 행렬 (Adjacency Matrix)
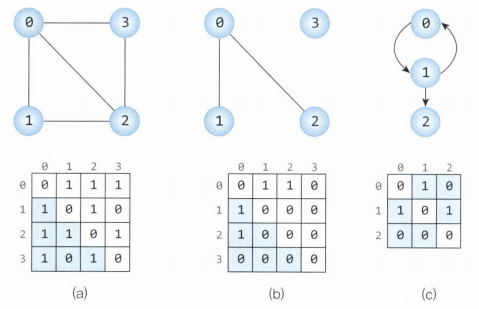
인접 행렬(adjacency matrix)은 2차원 배열을 사용하여 그래프를 표현하는 방법입니다.
그래프의 정점 수가 n이라면, n × n 크기의 2차원 배열 M을 생성하고,
정점 i와 j를 연결하는 간선이 존재할 경우 M[i][j] 값을 1로 설정합니다.
특징
- 자기 자신과의 간선(자가 간선)은 허용하지 않으므로,
인접 행렬의 대각선 성분은 모두 0으로 표시됩니다. - 무방향 그래프의 경우,
정점i와j가 연결되면M[i][j]와M[j][i]가 대칭적으로 1이 됩니다. - 방향 그래프의 경우,
정점i에서j로의 간선이 있을 때만M[i][j] = 1로 표시되며,
일반적으로 대칭이 아닙니다.
인접 리스트
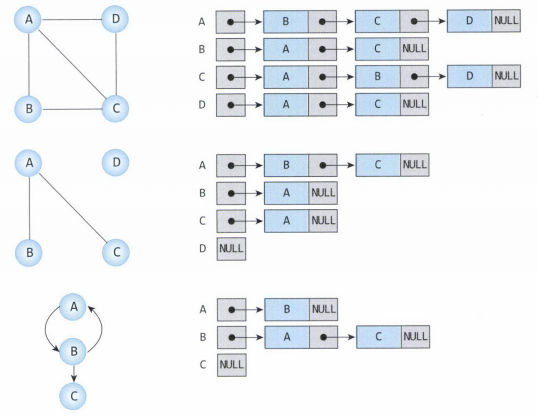
인접 리스트(adjacency list)는 그래프를 효율적으로 표현하는 방법으로,
각 정점에 인접한 정점들을 연결 리스트 형태로 저장하는 방식입니다.
특징
- 각 정점은 헤더 노드를 가지며, 이 헤더 노드들은 배열로 구성되어 있습니다.
- 정점 번호를 배열의 인덱스로 사용하면, 해당 정점의 연결 리스트에 쉽게 접근할 수 있습니다.
- 무방향 그래프의 경우, 간선 (i, j)는
- 정점 i의 연결 리스트에 j,
- 정점 j의 연결 리스트에 i
를 각각 추가하여 양방향으로 표현됩니다.
- 인접 정점이 연결 리스트에 추가되는 순서에 따라 리스트 내 정점의 순서가 달라질 수 있습니다.
그래프 탐색 알고리즘
그래프 탐색은 모든 정점을 한 번씩 방문하는 과정입니다.
대표적인 두 가지 방법은 DFS(깊이 우선 탐색) 과 BFS(너비 우선 탐색) 입니다.
DFS (Depth-First Search)
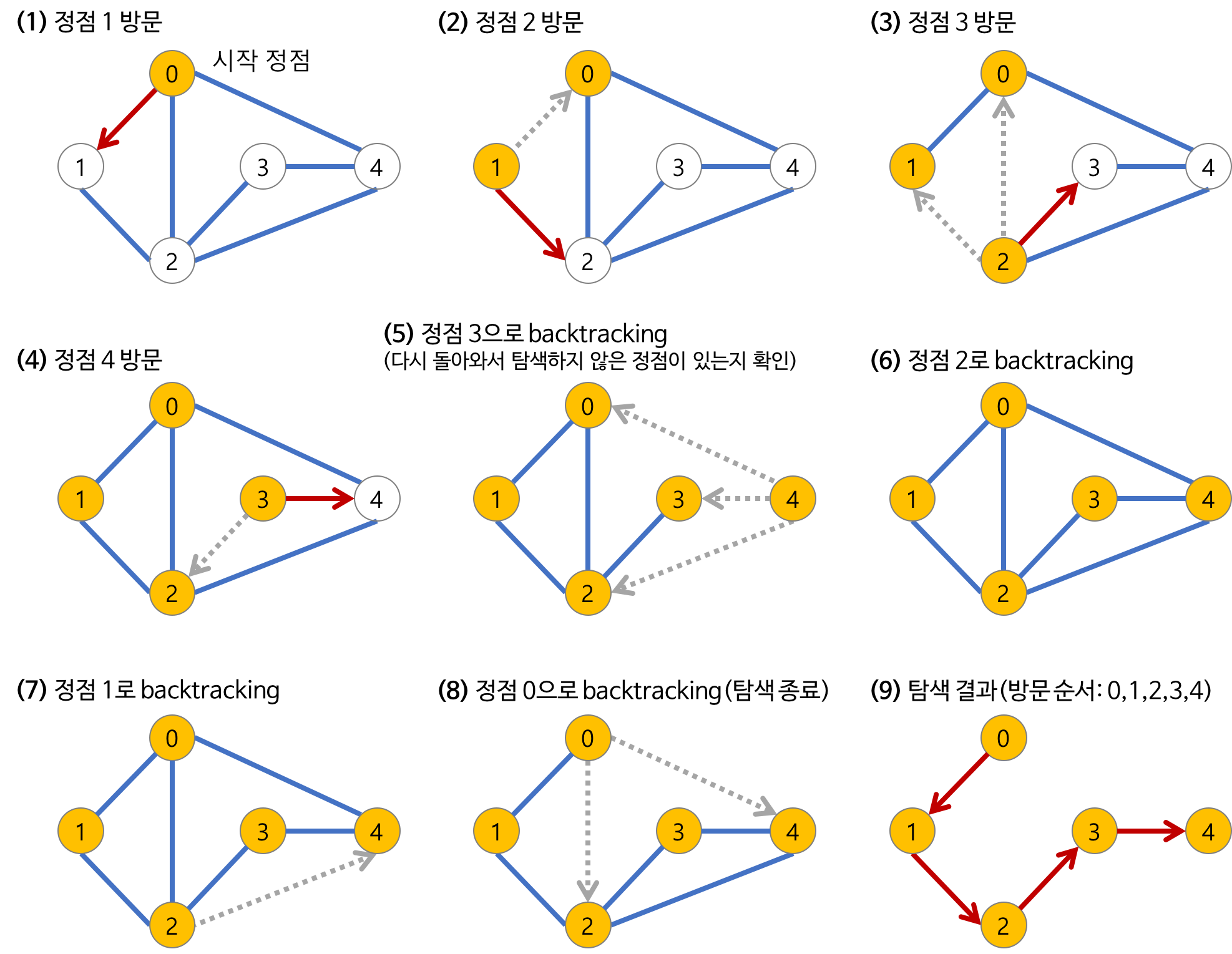
그래프의 시작 정점에서 출발하여 시작 정점 v를 방문했다고 표시합니다.
그 다음, v에 인접한 정점들 중 아직 방문하지 않은 정점 u를 선택합니다.
- 만약 방문하지 않은 인접 정점이 없다면 탐색을 종료합니다.
- 방문하지 않은 정점
u가 있다면, 그 정점을 새로운 시작 정점으로 하여 DFS를 재귀적으로 수행합니다. - 탐색이 끝나면 다시 이전 정점으로 돌아와,
인접한 정점들 중 방문하지 않은 정점이 있는지 확인합니다.
없으면 종료하고, 있다면 그 정점을 시작 정점으로 하여 DFS를 다시 수행합니다.
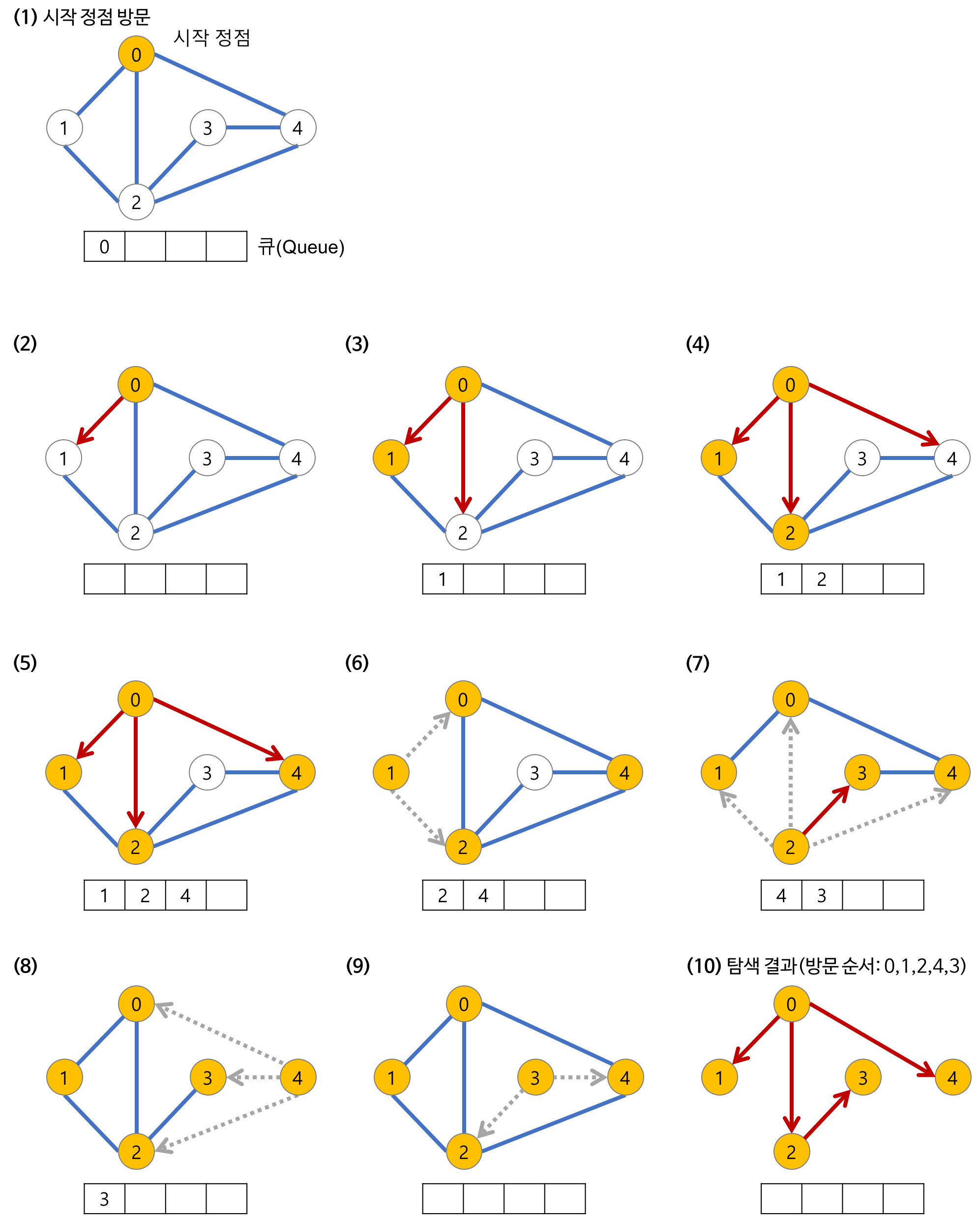
BFS (Breadth-First Search)
너비 우선 탐색(BFS)은 시작 정점으로부터 가까운 정점을 먼저 방문하고,
멀리 떨어져 있는 정점을 나중에 방문하는 그래프 순회 방법입니다.
탐색 과정
- 시작 정점을 큐(Queue)에 넣고, 방문 표시를 합니다.
- 큐에서 하나의 정점을 꺼내어, 그 정점에 인접한 정점들 중 방문하지 않은 정점을 모두 큐에 넣습니다.
- 큐가 비어 있을 때까지 이 과정을 반복합니다.
마무리
그래프는 단순한 자료구조 같지만, 지도 탐색, SNS 친구 추천, 네트워크 연결, 인공지능 경로 탐색 등
수많은 실제 서비스의 기반이 됩니다.
출처:
신민기씨 블로그
https://velog.io/@minki091212/%EA%B7%B8%EB%9E%98%ED%94%84Graph
