📌 Regression(회귀분석)

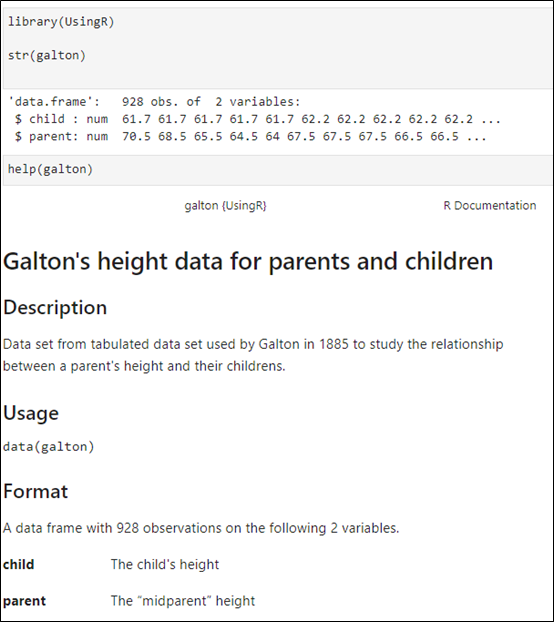
Galton의 데이터

• 패키지 UsingR
• 데이터 galton에는 부모의 키, 자식의 키에 대한 927개의 관측치가 있다.
• 부모의 키는 (아버지의 키 + 1.08*엄마의 키)/2
• 자료출처는 여기에
  

상관분석과 회귀분석

• 상관분석
  두 연속변량 사이에 상관관계가 있는지의 여부
• 회귀분석
  두 연속변량 사이에 함수 관계를 찾고, 예측할 수 있는 모형 찾기
• 단순선형회귀분석
  설명변수가 1개인 직선 모형
• 다중선형회귀분석
  설명변수가 여러 개인 일차 모형

📌 상관계수 성질

• 상관계수는 두 연속변량 X, Y의 선형 관계를 나타내주며 −1≤𝑟≤1이다.
• 𝑟>0일 때, X가 증가함에 따라, Y도 증가하는 경향이 있다.
• 𝑟<0일 때, X가 증가함에 따라, Y는 감소하는 경향이 있다.
• 𝑟=1이면, 모든 데이터가 기울기가 양수인 직선 위에 있다.
• 𝑟=−1이면, 모든 데이터가 기울기가 음수인 직선 위에 있다.
• 𝑟=0이면 선형관계가 없다.

---

💻 데이터 - 대리점의 광고비와 판매수익과의 관계

대리점	광고비(백만원)	판매수익(천만원)
1	2	8
2	3	9
3	6	18
4	4	17
5	7	21
6	4	14
7	8	27
8	6	22

c <- c(2,3,6,4,7,4,8,6)
s <- c(8,9,10,17,21,14,27,22)

df <- data.frame(cost=c, sales=s)

cor(df)

A matrix: 2 × 2 of type dbl
cost sales
cost 1.0000000 0.8167395
sales 0.8167395 1.0000000

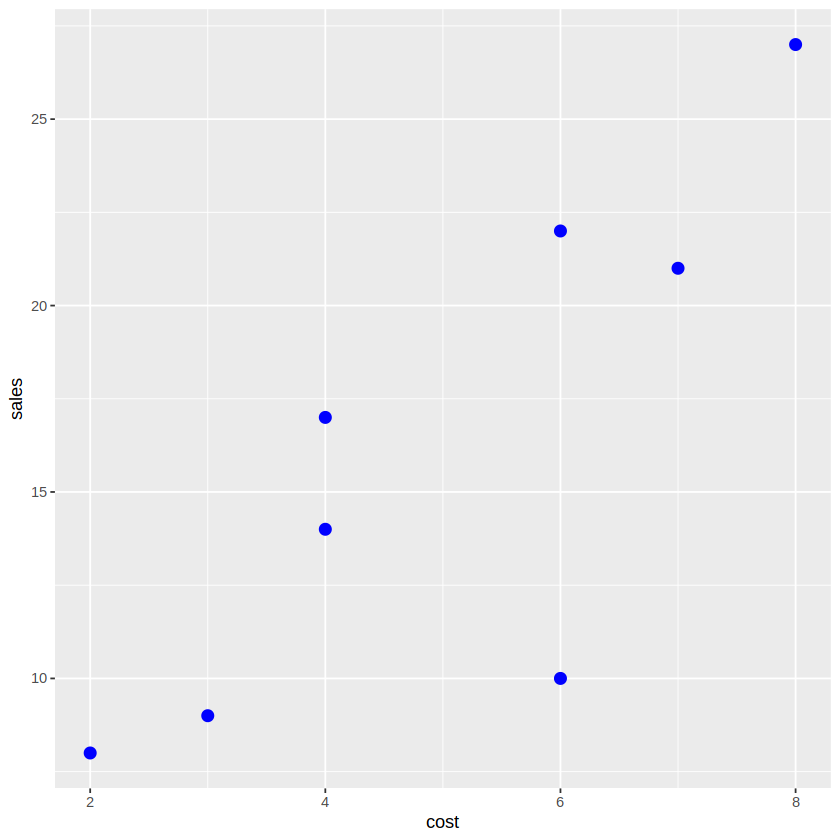
library(ggplot2)

p <- ggplot(df, aes(cost, sales))
p + geom_point(size=3, color='blue')

cor.test(df$cost, df$sales)

Pearson's product-moment correlation

data: df$cost and df$sales
t = 3.4672, df = 6, p-value = 0.01335
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2640181 0.9656486
sample estimates:
cor
0.8167395

• 상관계수는 0.9550718
• 귀무가설: 상관계수는 0이다.
• p-value는 0.0002192로 유의수준(0.05)보다 작으므로 유의하다.
• 상관계수가 0이라는 귀무가설을 기각.
• 즉, 상관계수는 0이 아니라고 할 수 있다.

---

📌 회귀분석(regression)

• 두 변량 X, Y 사이의 관계를 가장 잘 나타내주는 함수식 𝑦=𝑓(𝑥)을 찾아 modelling을 하고, 예측값을 구하는 과정
• 여기서 함수 𝑓(𝑥)가 일차식인 경우를 선형회귀분석이라 한다.
• 종속변수(반응변수) Y에 영향을 미치는 변수(독립변수)가 1개일 때, 단순회귀분석이라 한다.
• 특히, 독립변수가 1개이고 일차식인 경우를 단순선형회귀분석이라 한다.

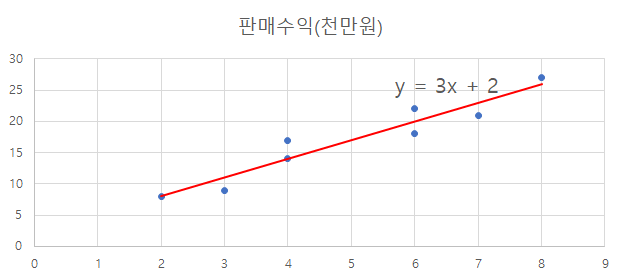
회귀직선 – 모델링 -> 예측치

• 회귀직선의 방정식은 𝒚=𝟑𝒙+𝟐로 이는 광고비가 1(백만원) 늘어나면, 판매수익이 3(천만원) 늘어난다는 것을 의미한다.
• 예측치: 예를 들어 광고비가 5(백만원)이라면 예상되는 판매수익은 𝟑×𝟓+𝟐=𝟏𝟕(천만원)

library(ggplot2)

p <- ggplot(df, aes(cost, sales))
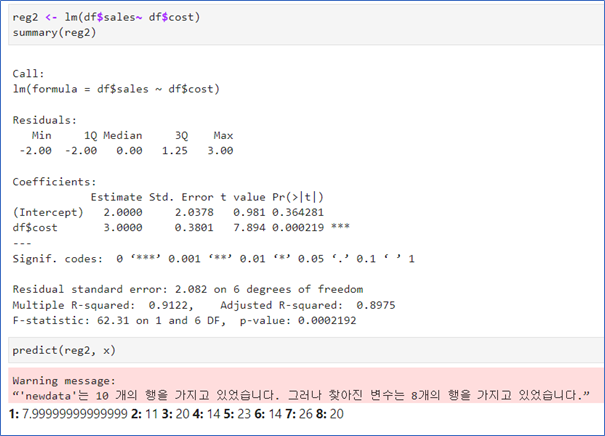
p + geom_point(size=3, color='blue') + geom_smooth(method = 'lm', formula = 'y~x')

reg <- lm(sales ~ cost, data=df)
reg
# 회귀분석
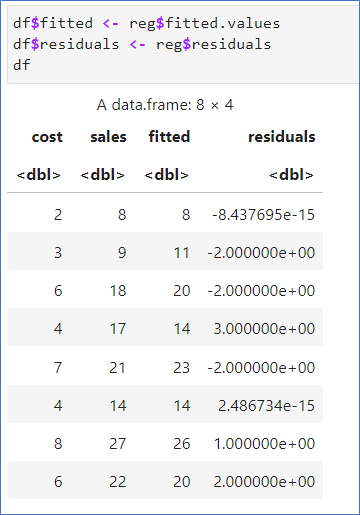
summary(reg)

Call:
lm(formula = sales ~ cost, data = df)

• Coefficients:
  (Intercept) cost
  2.333 2.733

• lm(종속변수 ~ 독립변수)
• 단순선형회귀 분석의 결과 y절편은 2, 기울기는 3
• R 제곱(결정계수)의 값은 0.9122
• 결정계수의 값이 1에 가까울수록 모형이 적합

📌 R을 이용한 회귀분석 – lm(), 회귀직선그리기

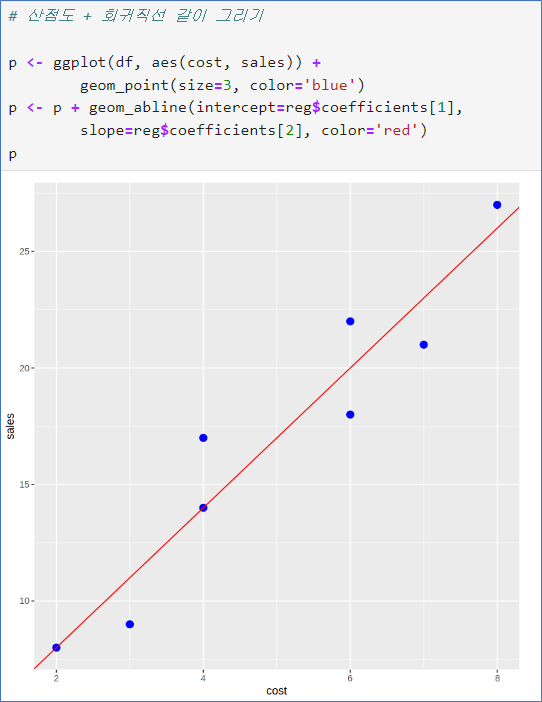
• 예측치(fitted.values) 회귀직선 상의 값
• 잔차(residuals) 관측치와 예측치의 차
  

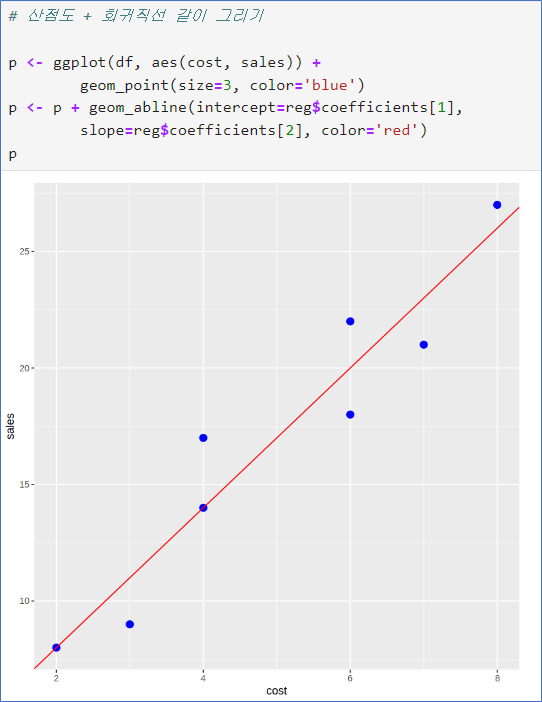
회귀직선그리기

• 회귀직선의 계수는 reg$coefficients에

• 첫번째가 y절편

• 두번째가 기울기

• geom_abline()은 직선을 y절편과 기울기로 그려주는 함수

• 회귀직선의 계수는 reg$coefficients에

• 첫번째가 y절편

• 두번째가 기울기

• geom_abline()은 직선을 y절편과 기울기로 그려주는 함수

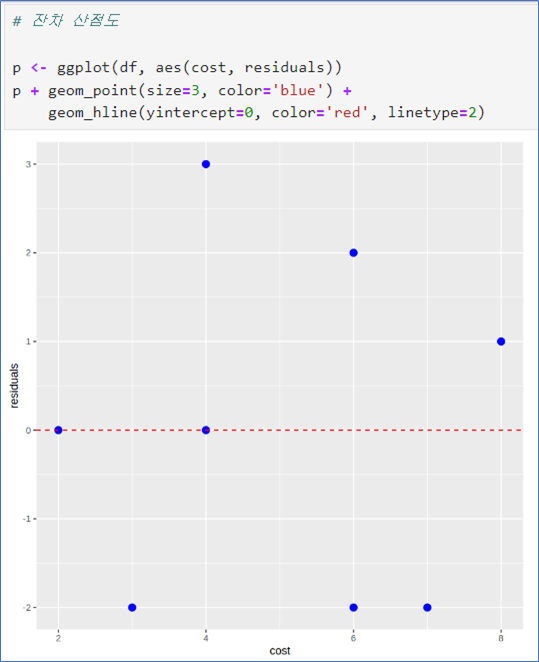
잔차 산점도

• 잔차의 산점도가 일정한 패턴을 나타내면 모형 부적합
• geom_hline()은 수평선
  

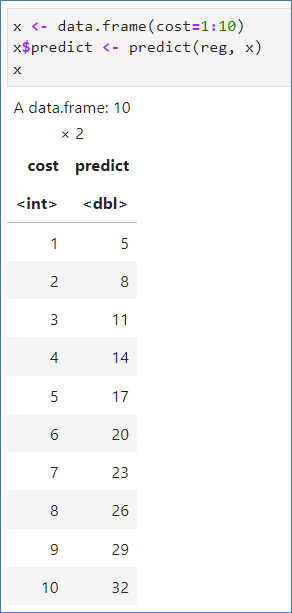
예측치 구하기 – predict()

• 예측치
• cost가 5일 때의 예측치는 17
• cost가 10일 때의 예측치는 32
• lm(df$y ~ lm$x)를 사용하면 predict에서 에러가 남
  

🚀 주의

회귀분석 lm 사용시 lm(y ~ x, data=df)
위와 같이 하지 않으면 예측치를 구하지 못함

---

📌 결과해석

• 회귀직선의 방정식: 𝒚=𝟐+𝟑𝒙

• 광고비가 1(백만원) 늘어나면, 판매수익이 3(천만원) 늘어난다는 것을 의미한다.

• 예측치: 광고비가 5(백만원)이라면 예상되는 판매수익은 𝟐+𝟑×𝟓=𝟏𝟕(천만원)이다.

  ---

📌 비선형 회귀 분석

?women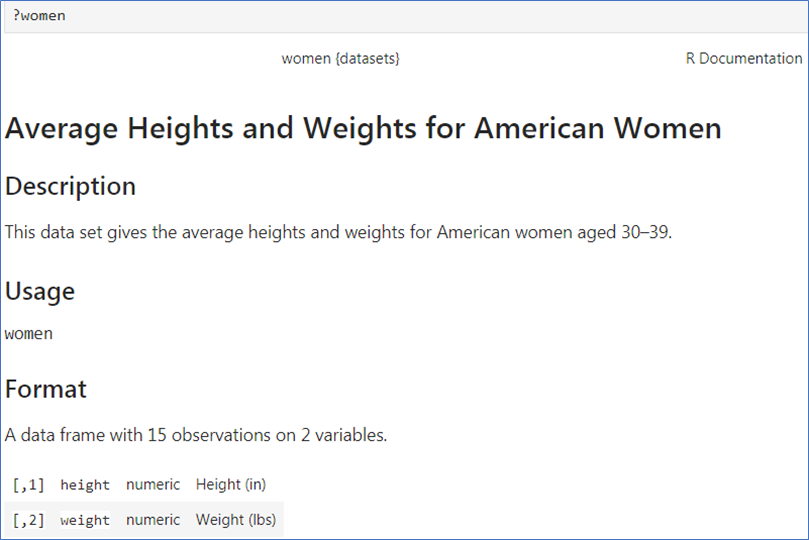

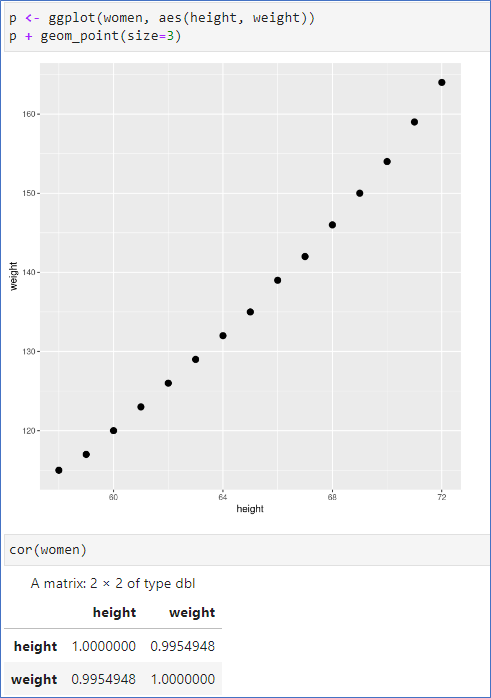
산점도

• 산점도 및 상관계수
• 상관계수는 0.995로 1에 매우 가까움
  

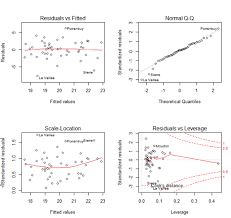
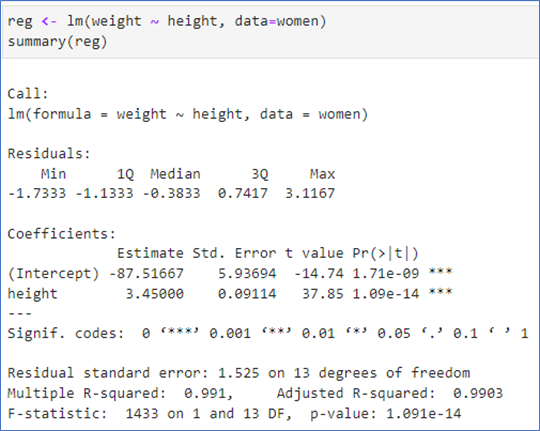
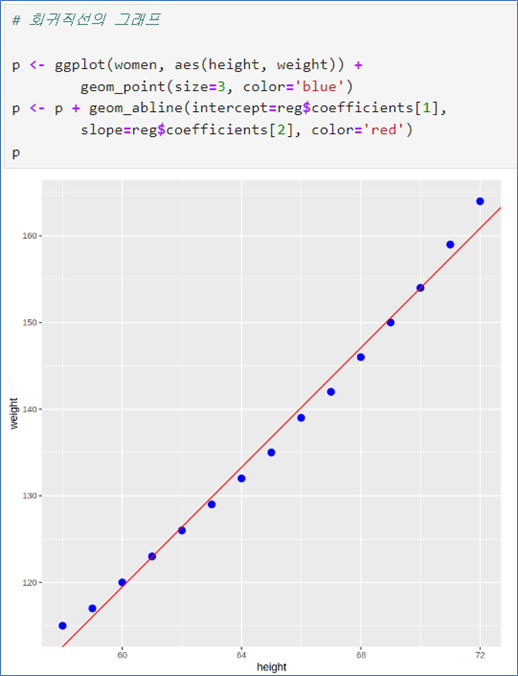
회귀분석, 회귀곡선 직선그래프, 잔차그래프

• y절편은 -87.5
• 기울기는 3.45
• R제곱은 0.991
• R제곱은 적절한 것으로 보임
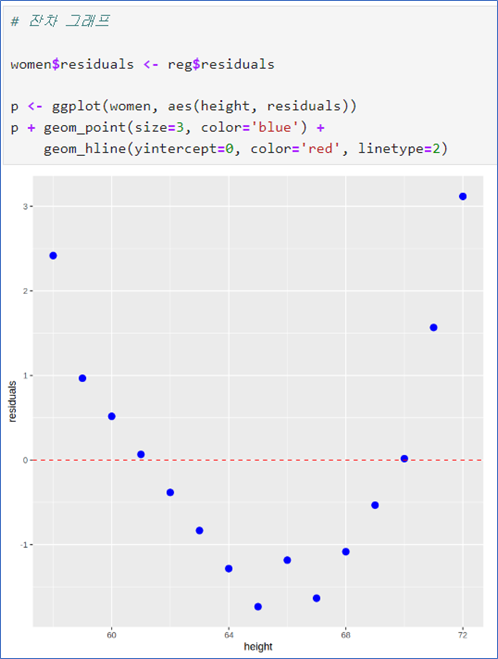
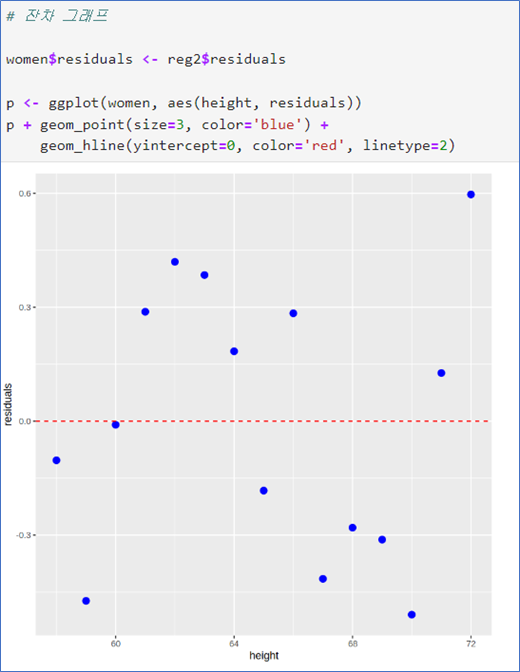
• 잔차의 그래프가 감소하다 증가하는 패턴을 보임.
• 모형 부적합
  

---

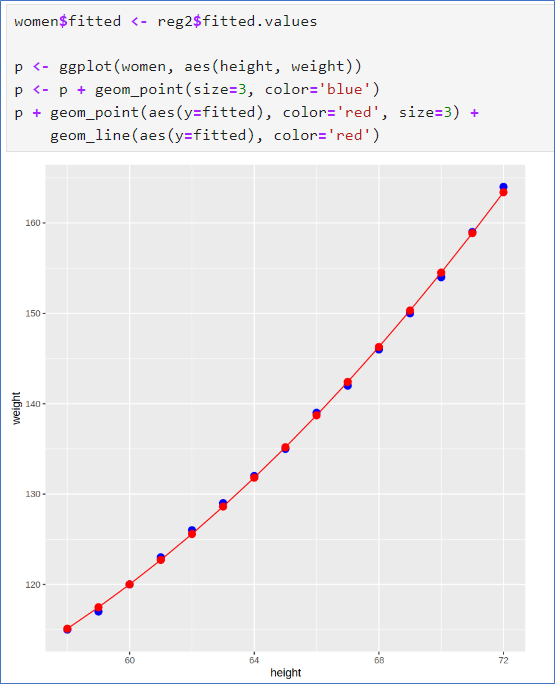
이차모형, 회귀곡선 곡선 그래프, 잔차 그래프

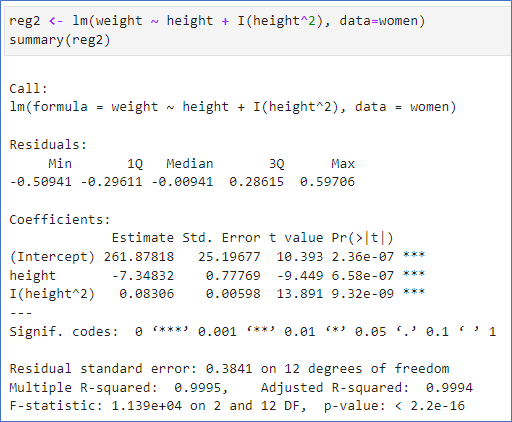
𝑦=𝛽_0+𝛽_1 𝑥+𝛽_2 𝑥^2+𝜖

• I( ) 함수를 이용하여 이차항 추가
• 상수항: 261.8
• 일차항: -7.34
• 이차항: 0.08
• R 제곱 = 0.9995
  

---

formula	구성 내용
y~x	y = a + bx 모형 구성
y~x-1	y = bx 절편이 없는 모형 구성
y~1/x	y = 절편항(평균)
y~x1+x2	y = a + b1x1 + b2x2 모형 구성
y~x1*x2	y = a + b1x1 + b2x2 + b3x1x2 (x1, x2의 교호작용을 고려한 모형 구성)
y~x1+x2+x1:x2	y = a + b1x1 + b2x2 + b3x1x2 (x1, x2의 교호작용을 고려한 모형 구성)
y~(x1+x2+x3)^2	y = a + b1x1 + b2x2 + b3x3 + b4x1x2 + b5x1x3 + b6x2x3
y~(x1+x2+x3)^3	y = a + b1x1 + b2x2 + b3x3 + b4x1x2 + b5x1x3 + b6x2x3 + b7x1x2x3
y~x1+I(x1^2)	y = a + b1x1 + b2x1^2
y~1/(1/x)	y = a + b1x
y~x1	z
y~., data=dd	y = a + b1x1 + b2x2 ... 모형 구성 (dd라는 이름의 data, 종속변수 y를 지정, 이외 모든 변수는 설명변수)