백준 - 1005번 : ACM Craft (C++)

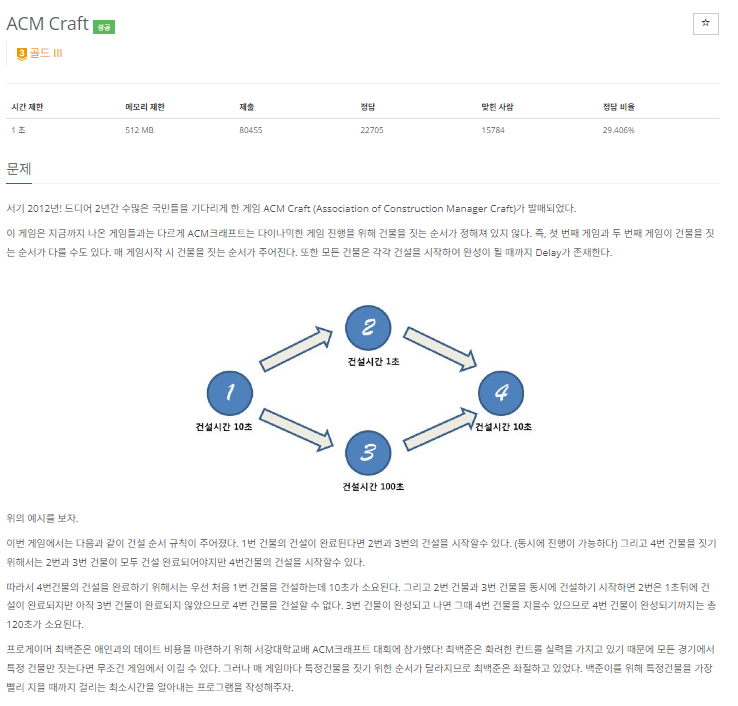
풀이 방법 : 위상 정렬 + DP

건물 중에 특정 건물들이 이미 건설되어 있어야만 건설 시작이 가능하기 때문에 선행 관계에 따라 순서를 파악해야 한다. 따라서 위상정렬을 사용해야 한다.
선행 건물이 있는 건물의 건설 시작을 할 수 있는 가장 최소 시간은 선행 건물들의 건설 시간 중 최댓값이 된다.
이들을 누적, 메모해나가며 최댓값을 구하면 원하는 건물을 짓기 위한 최소 시간이 될 것이다.

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

int InCnt[1001] = {};
int DP[1001] = {};
vector<int> vecTime;
vector<vector<int>> vecGraph;

int main()
{
	cin.tie(nullptr);
	cout.tie(nullptr);
	ios::sync_with_stdio(false);

	int T;
	cin >> T;

	while (T > 0)
	{
		--T;
		int N, K;
		cin >> N >> K;

		vecTime.resize(N + 1);

		for (int i = 1; i <= N; ++i)
		{
			cin >> vecTime[i];
			InCnt[i] = 0;
		}

		vecGraph = vector<vector<int>>(N + 1);

		for (int i = 0; i < K; ++i)
		{
			int Src, Dest;
			cin >> Src >> Dest;
			vecGraph[Src].push_back(Dest);
			++InCnt[Dest];
		}

		int Last;
		cin >> Last;

		queue<int> qVtx;

		for (int i = 1; i <= N; ++i)
		{
			if (InCnt[i] == 0)
				qVtx.push(i);
		}

		for (int i = 1; i <= N; ++i)
		{
			DP[i] = -1;
		}

		vector<int> vecVtx;
		while (!qVtx.empty())
		{
			int Cur = qVtx.front();
			vecVtx.push_back(Cur);
			qVtx.pop();

			int Time = max(DP[Cur] + vecTime[Cur], vecTime[Cur]);

			int Size = vecGraph[Cur].size();

			for (int i = 0; i < Size; ++i)
			{
				--InCnt[vecGraph[Cur][i]];

				DP[vecGraph[Cur][i]] = max(DP[vecGraph[Cur][i]], Time);

				if (InCnt[vecGraph[Cur][i]] == 0)
					qVtx.push(vecGraph[Cur][i]);

			}
		}

		cout << max(DP[Last] + vecTime[Last], vecTime[Last]) << '\n';

	}

}