백준 - 1507번 : 궁금한 민호 (C++)

풀이 방법 : 플로이드 - 워셜

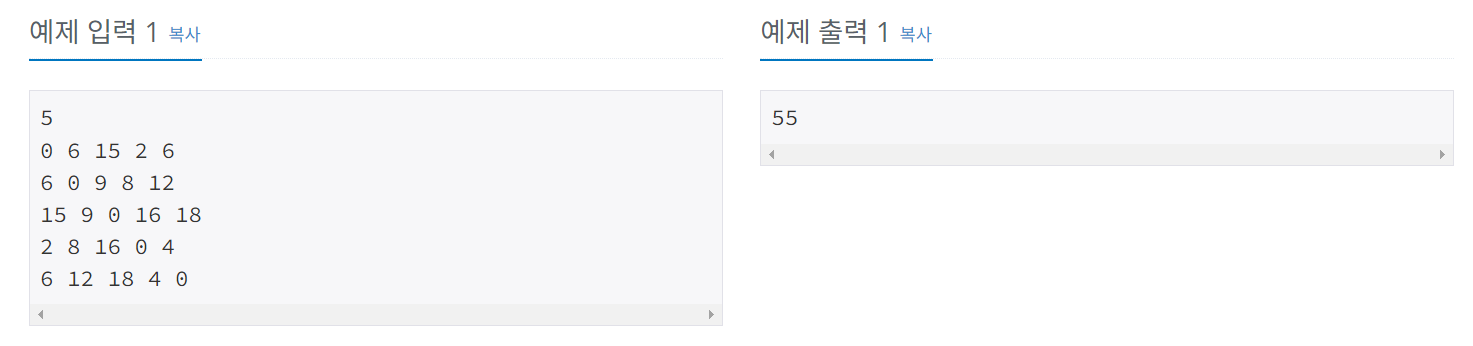
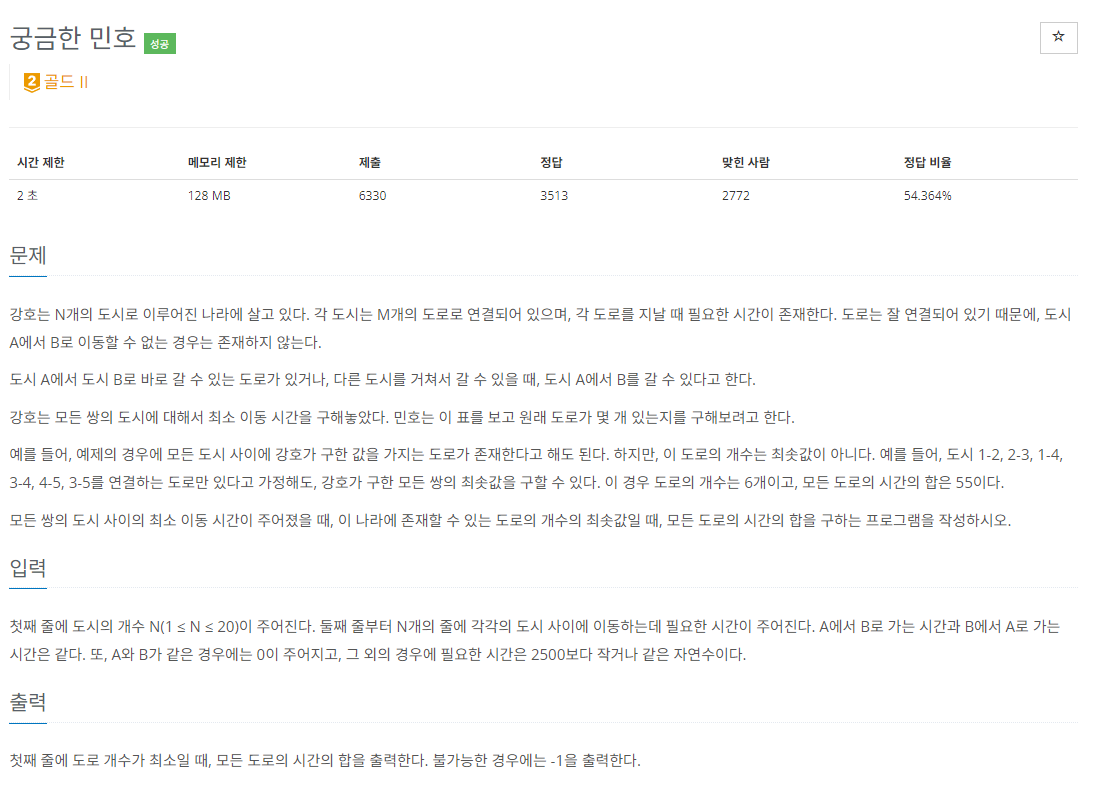
문제 설명을 잘 읽어보면 입력으로 주어지는 값들이 모든 쌍의 도시에 대해 최소 이동 시간들이라는 것을 알 수 있고 이 결과값들은 즉 플로이드 - 워셜 알고리즘에 의해 구해진 값과 동일한 값들이라는 것을 알 수 있다.

플로이드 - 워셜 알고리즘을 돌려서 Time[i][j] == Time[i][k] + Time[k][j] 인 부분을 찾는다면 i - j 이동 시간이 k를 경유해서 가는 것이 더 빠르다는 얘기이므로 i - k, j - k 도로만 있고 i - j 도로는 없어도 된다는 것이 된다.

이것에 해당되는 i - j 도로에 대해 마킹 해주고 나중에 이를 제외하고 시간의 총합을 구해주면 문제에서 원하는 답이 된다. 두 번 카운팅 될 것이니 2로 나눠주는 것도 잊지 말아야한다.

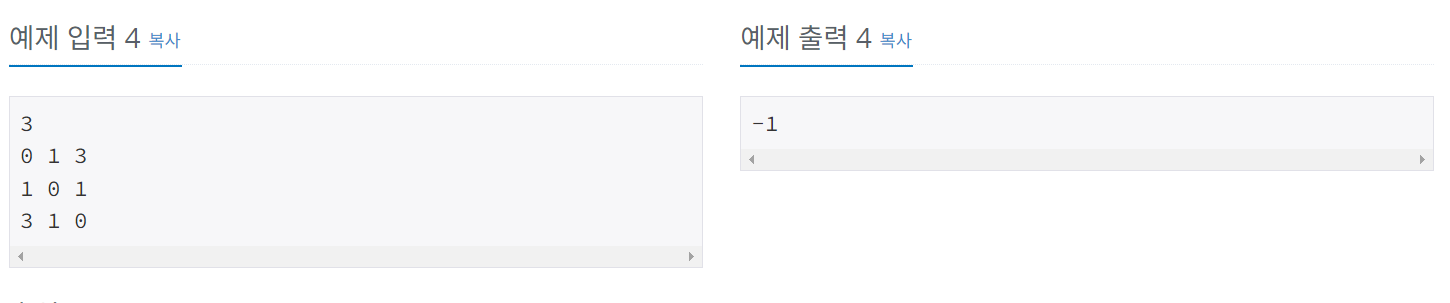
만약 알고리즘을 돌리던 도중 예제 입력 4와 같이 Time[i][j] > Time[i][k] + Time[k][j]인 케이스가 발생한다면 모든 쌍의 도시에 대해 최소 이동 시간이 주어진다는 내용에 모순이 되므로 이는 불가능한 경우가 된다. 이 경우에는 문제에서 요구하는 대로 -1을 출력해주자

당연히 i == j, j == k, i == k 인 부분은 제외해야한다. 포함한다면 결국에는 같은 도로끼리 비교하는 경우가 생기기 때문에 필요한 도로임에도 최종 총합에서 제외되어버린다.

#include <iostream>

using namespace std;

int Time[21][21] = {};
bool Check[21][21] = {};

int main()
{
	cin.tie(nullptr);
	cout.tie(nullptr);
	ios::sync_with_stdio(false);

	int N;
	cin >> N;

	for (int i = 1; i <= N; ++i)
	{
		for (int j = 1; j <= N; ++j)
		{
			cin >> Time[i][j];
		}
	}

	if (N == 1)
	{
		cout << 0;
		return 0;
	}
	
	bool Enable = true;

	for (int k = 1; k <= N; ++k)
	{
		for (int i = 1; i <= N; ++i)
		{
			for (int j = 1; j <= N; ++j)
			{
				if (i == k || i == j || j == k)
					continue;

				if (Time[i][j] == Time[i][k] + Time[k][j])
				{
					Check[i][j] = true;
				}

				else if (Time[i][j] > Time[i][k] + Time[k][j])
				{
					Enable = false;
				}
				
			}
		}
	}

	int Sum = 0;

	for (int i = 1; i <= N; ++i)
	{
		for (int j = 1; j <= N; ++j)
		{
			if(!Check[i][j])
				Sum += Time[i][j];
		}
	}

	if (!Enable)
		cout << -1;

	else
		cout << Sum / 2;

}

플로이드 - 워셜 알고리즘의 연산 과정을 이해하고 역추적 해야 한다는 점이 너무 재미있었던 문제