-
모델링이란, 대용량의 데이터로부터 이들 데이터 내에 존재하는 관계, 패턴, 규칙 등을 탐색하고 변수들 간의 관련성을 찾아내어 모형화함으로써 유용한 지식을 추출하는 일련의 과정을 말한다.
-
모델링의 종류:
Data 모델링: 지도학습, 비지도학습
회귀: 주어진 데이터에 근거하여 모델을 만들고 이 모델을 이용하여 새로운 케이스에 대하여 예측 (강도, 온도)
분류: 일련의 범주가 사전에 분류되어있고 특정 Case가 어디에 속하는지를 결정 (양품/불량, 스팸/정상)
군집: 여러 속성의 데이터를 비교하여 유사한 속성을 갖는 데이터를 그룹화시키는것 (고객 세분화)
연관: 한 패턴의 출현이 다른 패턴의 출현을 암시하는 특성이나 항목간의 관계를 파악 (장바구니 분석)
1. 회귀분석
정의 : 연속형 목표변수와 다양한 설명변수 관계를 모형화하여 목표변수를 분석, 예측
목적 : 목표변수에 영향을 미치는 설명변수를 찾고 목표변수의 값을 예측하자
ex) 광고 지출액에 따른 매출액, 담배 판매량에 따른 폐암 환자수
기본가정: 선형성, 정규성, 등분산성, 독립성
특징 : 표준화가 필요하다. 기본 가정이 요구된다.
종류:
Linear Regression | 연속형 목표변수, 값 예측, 선형방정식 함수표현, 최소자승법, f검정, t검정
Logistic Regression | 범주형 목표변수, 분류, 사후확률예측, 연결함수를 이용한 관계표현, 최대우도법, 카이제곱검정
단순선형회귀 | 설명변수 1개, 1차항 y=A+Bx
다중선형회귀 | 설명변수 2개이상, 1차항 y= A+ Bx + Cx + DX...
비선형 회귀 | 설명변수 2개이상, 1차항 및 다차항 y= A+ Bx + Cx2 + Dx3 ...
다중로지스틱회귀 | 설명변수 2개이상, 연결함수
2. 단순선형 회귀분석
설명변수가 1개이고 목표변수와 선형관계를 갖는 회귀모델
y = b0 + b1x + 앱실론
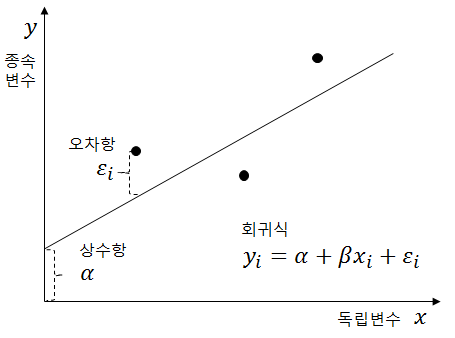
- 회귀계수는 최소자승법을 활용하여 추정한다.
- 잔차항은 정규분포를 따른다.
- 잔차항의 평균은 0이다.
- 잔차항은 등분산이다.
- 잔차항은 서로 독립이다.
- 경향성 확인 : 산점도, 상관분석
- Ordinary Least Squares에 의한 회귀계수 추정 ==> 잔차의 제곱의 합이 최소가 되도록 함
- SST = SSR(설명변수에 의해 설명되는 변동) + SSE(오차로 인해 설명되지 않는 변동)
- 회귀계수 계산 : 최소자승법을 활용하여 기울기와 Y 절편 계산
- 추정된 회귀계수와 표준오차를 이용한 회귀계수 유의성 검정 (T-Test)
- 귀무가설: 기울기없음, 대립가설: 기울기있음
- 모델 적합성 확인 : F 검정 ==> 회귀계수가 0이 아니면 모델은 적합하다.
- 결정계수 R2 : 전체 변동 중에서 모델에 의해 설명되는 변동의 크기, 0~1값
3. 다중선형 회귀분석
목표변수와 2개이상의 설명변수와의 선형관계를 모델링한다.
회귀계수는 최소자승법 (Least Squares Method)를 활용하여 도출한다.
설명변수 간의 다중공선성을 확인해야한다.
- 분석 절차
1) 경향성 확인 : 변수 간의 상환성 확인(산점도, 상관관계), 주요 변수 이해 및 산정
2) 모델링 : 최소자승법으로 회귀계수 계산, 설명변수 간 다중 공선성 확인, 회귀계수 유의성 검정, 목표변수에 영향을 미치는 설명변수 확인
3) 회귀모델의 적합성 확인 ( 표준오차, 결정계수 ), 모델유형의 적합성을 나타내는 ANOVA 분석결과 확인
4) 오차의 기본 가정사항 확인 (정규성, 등분산성, 독립성)
5) 모델 확정
-
최소자승법으로 회귀계수 산정 : 잔차의 제곱합이 최소가 되는 적합선을 찾는다.
-
회귀계수 유의성 검정: 귀무가설-기울기0, 대립가설-기울기0아닌게잇음 ====> T-test 검정
-
ANOVA 검정 : 분산분석 F-검정 활용하여 모델 유의성 검정
가설: 모델에 유의한 회귀계수가 존재하는가? -> 적어도 하나 이상의 회귀계수가 0이아니면 모델은 적합하다. -
결정계수 : 다중선형 회귀분석은 수정결정계수 Adjusted R2로 판단한다.
-
추정의 표준오차 : 잔차들의 표준편차
-
다중공선성 : 설명변수 간의 선형관계가 높아 발생하는 문제
진단 : 산점도 또는 상관계수를 확인한다.
분산팽창계수(VIF)를 확인한다. 10보다 크면 다중공선성이 존재한다.
- 변수 선택법
1) 전진선택법
2) 후진제거법
3) 단계적 방법
4) 모든 가능한 회귀
4. 다중선형 회귀분석 - 규제화
왜? 과대적합을 방지하기 위해서
회귀 모델의 회귀계수가 가질 수 있는 값에 대한 제약조건을 부여하여 모델의 분산을 감소시키고 모델의 일반화 성능을 높이는 기법
- 평균제곱오차를 최소화하는 최소자승법을 적용하면서 계수에 제약조건을 추가로 적용한다.
- 변수 선택 - 중요한 변수는 선택하고 중요하지 않은 변수는 제거한다.
- 계수 축소 - 덜 중요한 변수의 해당 계수 절대값을 낮춘다.
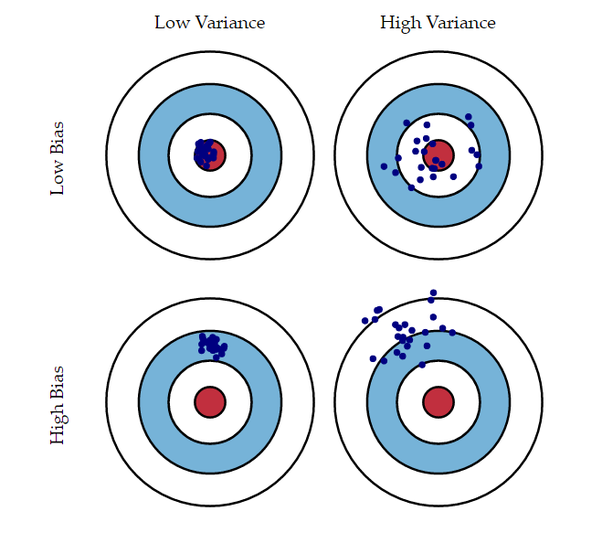
- 편향 분석 trade -off
편향 : 예측값의 평균과 실제값의 차이
분산: 예측값과 예측지 평균과의 차이 제곱
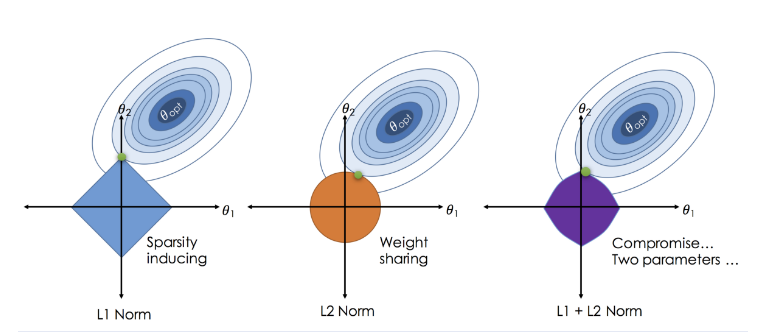
회귀분석 규제화 종류
1. 능형 회귀분석 (Ridge) | L2규제(제곱합), 회귀계수를 가능한 작게 만든다.
2. LASSO 회귀분석 | L1 규제(절대값), 변수를 선택할 수 있다.
3. Elastic Net Regression | L1+L2 규제(둘다)
5. 비선형 회귀분석
목표변수와 설명변수 간의 비선형 관계를 탐색하는 모델로, 선형 회귀분석과 달리 설명변수에 대한 최적의 다차항을 선택하는 기준이 없어 반복적으로 최적의 관계를 찾고 모델을 수정해야 한다.