
#2023. 신기한 소수
작성일시: 2022년 12월 16일 오전 1:57
문제
수빈이가 세상에서 가장 좋아하는 것은 소수이고, 취미는 소수를 가지고 노는 것이다. 요즘 수빈이가 가장 관심있어 하는 소수는 7331이다.
7331은 소수인데, 신기하게도 733도 소수이고, 73도 소수이고, 7도 소수이다. 즉, 왼쪽부터 1자리, 2자리, 3자리, 4자리 수 모두 소수이다! 수빈이는 이런 숫자를 신기한 소수라고 이름 붙였다.
수빈이는 N자리의 숫자 중에서 어떤 수들이 신기한 소수인지 궁금해졌다. N이 주어졌을 때, 수빈이를 위해 N자리 신기한 소수를 모두 찾아보자.
입력
첫째 줄에 N(1 ≤ N ≤ 8)이 주어진다.
4
출력
N자리 수 중에서 신기한 소수를 오름차순으로 정렬해서 한 줄에 하나씩 출력한다.
2333 2339 2393 2399 2939 3119 3137 3733 3739 3793 3797 5939 7193 7331 7333 7393
분석
방향성을 잡아보자. 우선, 소수를 구하는 for문 또는 def함수문을 만들어야 한다.
한 자리수만 구하는 것이 아니라,
왼쪽부터 1의 자리를 포함해서 2자리, 3자리, 4자리 모두 소수여야 한다. 따라서 각 자리수별로도 소수인지 구별을 해야 한다.
함수를 반복하여 호출하는 재귀함수가 필요하다.
소수
소수란, 2보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어떨어지지 않는 자연수, 즉 1과 자기자신만을 약수로 가지는 수를 의미한다.
예를 들어 '6'은 1,2,3,6으로 나누어 떨어져서 소수가 아니고, '7'은 1과 7을 제외하고는 나누어 떨어지지 않아서 소수이다.
소수 구하기 알고리즘
주어진 수가 소수인지 판별하는 문제는 소수에 관련된 가장 기초적인 문제이다.
방법 1. 간단한 방법
- X가 주어졌을 때 X를 2부터 X - 1까지의 모든 수로 나누어 본다.
- 2~x-1까지 순회하면서 x의 약수가 있는지 확인한다. 약수가 하나도 없으면 x가 소수라는 사실을 알 수 있다.
def is_prime_number(x):
# 2부터 (x - 1)까지의 모든 수를 확인하며
for i in range(2, x):
# x가 해당 수로 나누어떨어진다면
if x % i == 0:
return False # 소수 아님
return True
print(is_prime_number(4))
print(is_prime_number(7))
- 2부터 판별하는 수 전까지 나눠보고 나머지가 0이 안 나온다면 소수로 정의하는 풀이
- 따라서, 해당 수까지 모두 확인해야 함
- 시간복잡도 : O(N)
- 가장 원초적인 방법
방법 2. 방법1에 대한 개선방법 (절반)
위 알고리즘을 개선한 알고리즘이다. 해당 숫자의 절반까지만 확인한다. 다음 예시를 보자.
- 1 X 16 = 16
- 2 X 8 = 16
- 4 X 4 = 16
- 8 X 2 = 16
- 16 X 1 = 16
절반인 4이후에는 숫자들이 반복되는 것을 확인할 수 있다.
따라서 가운데 약수까지만 '나누어떨어지는지' 확인하면 된다.
- 시간복잡도 : O(N)
import math
# 소수 판별 함수
def is_prime_number(x):
# 2부터 x의 절반까지의 모든 수를 확인하며
for i in range(2, x//2+ 1):
# x가 해당 수로 나누어 떨어진다면
if x % i == 0:
return False # 소수가 아님
return True- 이 방법 말고도 최적화할 수 있는 방법은 여러 가지가 있따.
- 2와 3을 제외한 소수는 6k+1, 6k-1의 형태를 띈다는 사실 이용하기
- 작은 소수들의 목록을 미리 만들어놨다가 이들로 먼저 나누는 방법을 시도해보기
- 등이 있다. 하지만 이와 같은 최적화는 자주 사용하지 않는다.
- 판단해야 할 수가 많지 않을 때는 단순한 코드로 충분하지만,
- 판단해야 할 수가 많을 때는 해당 방식으로 아무리 최적해봐야 소용 없기 때문이다.
- 많은 수에 대해 소수 판단을 해야 할 때는 대개 (방법3)
**에라토스테네스의 체**를 이용해서 특정 범위의 숫자들에 미리 소수 판단을 해두는 방법을 사용하게 된다.
방법 3. 방법2를 활용한 방법 (제곱근)
- 두 번째 방법의 원리를 인용해 해당 숫자의 제곱근까지 확인하는 방법이다. 이 원리는 약수를 중심으로 구한다.
- 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
1:80, 2:40, 4:20, 5:16, 8:10이다. 이때 √80은 대량 8.xxx이 나온다. 즉, 시간 복잡도는 O(√N)이 된다.
- 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
import math
# 소수 판별 함수
def is_prime_number(x):
# 2부터 x의 절반까지의 모든 수를 확인하며
for i in range(2, int(math.sqrt(n))+ 1):
# x가 해당 수로 나누어 떨어진다면
if x % i == 0:
return False # 소수가 아님
return True방법4. 에라토스테네스의 체 알고리즘
출처 : https://loosie.tistory.com/267
- 에라토스테네스의 체 알고리즘은 여러 개의 수가 소수인지 아닌지를 판별할 때 사용하는 대표적인 알고리즘이다
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
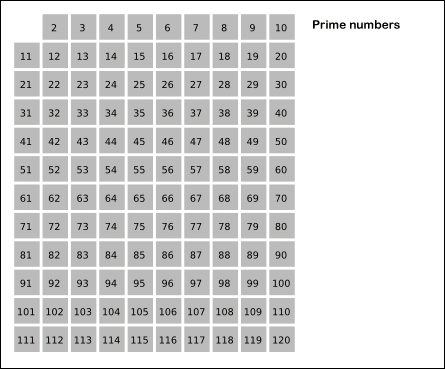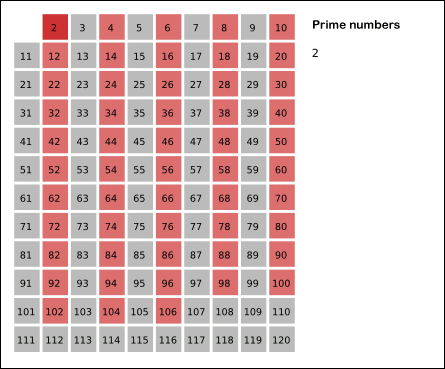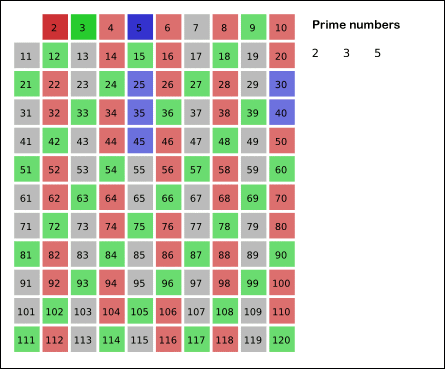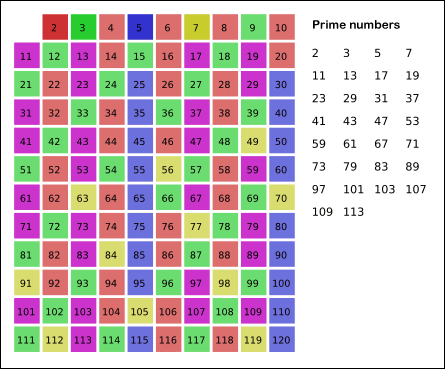
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
구현
- 지워지지 않은 수를 찾을 때 n이 아니라 까지만 찾는다.
이것은 위의 소수 판정 알고리즘과 똑같은 최적화 방식이다. - 또한, i의 배수들을 모두 지울 때 에서 시작하는 것이 아니라 에서 시작하는 것이다. 는 이미 2의 배수를 지울 때 지워졌고 는 이미 3의 배수를 지울 때 지워졌기 때문이다.
- (k < i)까지는 이미 검사되었으므로 j시작 값은 에서 로 개선할 수 있다. (k의 최댓값은 i-1이므로)
- 만약 isPrime[i]가 true이면, i 이후의 i 배수는 약수로 i를 가지고 있는 것이 되므로 모두 true값을 준다.
- 만약 isPrime[i]가 false이면, i는 이미 소수가 아니므로 i의 배수 역시 소수가 아니게 된다. 그러므로 검사할 필요가 없다.
import math
n = 1000 # 2부터 1000까지의 모든 수에 대하여 소수 판별
array = [True for i in range(n + 1)] # 처음엔 모든 수가 소수(True)인 것으로 초기화(0과 1은 제와)
# 에라토스테네스의 체 알고리즘
for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인하며
if array[i] == True: # i가 소수인 경우(남은 수인 경우)
# i를 제외한 i의 모든 배수를 지우기
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# 모든 소수 출력
for i in range(2, n + 1):
if array[i]:
print(i, end=" ")- 시간복잡도 : O(NloglogN)
- 메모리가 많이 필요하다는 단점
접근법 : DFS
풀이
풀이1
import sys
sys.stdin = open('input.txt')
N = int(input())
nums =[1,2,3,5,7,9] # 마지막 수가 짝수이면 소수가 아니니 빼주는데
# 2는 첫자리로는 가능합니다.
def dfs(strnum):
if len(strnum)==N: # N자리 숫자면
print(strnum) # 출력을 해줍니다.
return # 함수 끝
for n in nums: # 1,2,3,5,7,9 들을
newnum = strnum + str(n) # 하나씩 뒷자리로 넣어봅니다.
if sosu(int(newnum)): # 이숫자가 소수인지 판단해봅니다.
dfs(newnum) # 소수이면 dfs로 들어갑니다.
def sosu(num): # 소수 판단하기
if (num==1): # 1은 소수가 아닙니다
return False
for i in range(2, int(num**0.5) +1): #2부터 num의 제곱근까지
if num%i ==0: # 하나씩 나눠보다가 나눠지는 값이 있으면
return False # 소수가 아닌것
return True # 다 통과하면 소수
dfs("")- dfs의 종료조건 : 길이가 입력받은 N과 같을 때
- 소수 구하는 것은 에라토스테네스의 체를 사용하면 메모리초과가 뜬다. 따라서 방법3인 제곱근을 이용하는 방법을 사용해 함수(
sosu)로 만들어준다. - 소수로 올 수 있는 모든 수를 리스트에 담는다. 조금이라도 최적화하기 위해서이다. 이때 1은 첫째자리로 올 수 없기 때문에
sosu에서 예외처리한다. - num에 있는 수들을
dfs에서sosu함수를 이용해서 소수인지 확인한 후, string에 추가한다.
풀이2
import sys
input = sys.stdin.readline
n = int(input())
def checkPrimeNum(check_number):
#에라토스테네스의 체로 소수인지 확인
for i in range(2, int(check_number**0.5)+1):
if int(check_number) % i == 0:
return False
return True
def dfs(num):
# 목표 길이 도달 시 멈춤
if len(str(num))==n:
print(num)
else:
for i in range(10):
temp = num * 10 + i
# 10곱하고 i 더해서 자릿수 늘린 수가 소수일때만
# dfs로 다음 자릿수 확인 넘김
if checkPrimeNum(temp) == True:
dfs(temp)
# 맨마지막으로 맨 앞자리를 봤을 떄 소수여야하므로
# 일의자리숫자중에 소수로 시작을 한다.
dfs(2)
dfs(3)
dfs(5)
dfs(7)첫번째 풀이방법과 같은 형식이다.
첫 숫자는 2,3,5,7로만 시작하기 때문에 dfs로 2, 3, 5, 7 각각 따로 호출한다. 그 다음은 dfs함수에서 소수 구한 후에 10을 곱하여 자릿수도 늘리는 방법을 이용한다.
출처 : https://velog.io/@jpdev/2023.-신기한-소수
풀이3
def check(num):
for i in range(2, int(int(num)**0.5)+1):
if int(num) % i ==0:
return
if len(num) == n:
print(num)
return
for p in prime:
find(num+p)
n = int(input())
start = ['2', '3', '5', '7']
prime = ['1', '3', '7', '9']
for s in start:
check(s)- check함수 안에서 체크하는 숫자의 제곱근이 되기 전의 수들을 구해서 나눠준다. 만약에 나뉘었을 때 소수가 아니면 함수를 나간다.
- 체크하는 숫자가 내가 원하는 숫자자리수와 맞는지 확인하고 아니라면 함수 나간다.
- 맨 마지막에 뒷자리에 올 수 있는 숫자들 (
prime)을 하나씩 넣어주면서 체크한다. - 예를 들어서 시작을 2로 시작할 때, 1, 3, 7, 9를 하나씩 붙여보고, 21에 1, 3, 7, 9를 붙여보고 체크하는 방식이다.
회고
- 소수 구하는 방법에 대해 알 수 있었다.
- 재귀함수에 대해서 조금이라도 이해할 수 있었다
- 내가 준비했지만 다시 복습해야 할 것 같다.
