Image Resizing

이미지의 해상도를 축소시키거나 늘릴 때 사용하는 기술이다.

확대와 축소는 단순하게 N배와 1/N배로 하는 로직을 떠올릴 수 있을 것이다.

Interpolation(Upsacling)

근처의 이웃과 비교하면 된다.

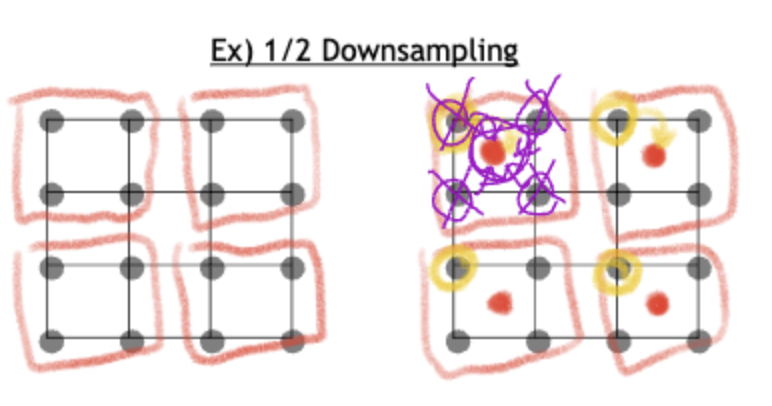
위 방식은 1/2 Downsampling 과정에서 2 x 2의 픽셀의 평균값을 대표 픽셀로 지정하는 방식이다.

이러한 방법은 Interpolation으로 여러가지 방법이 있다.

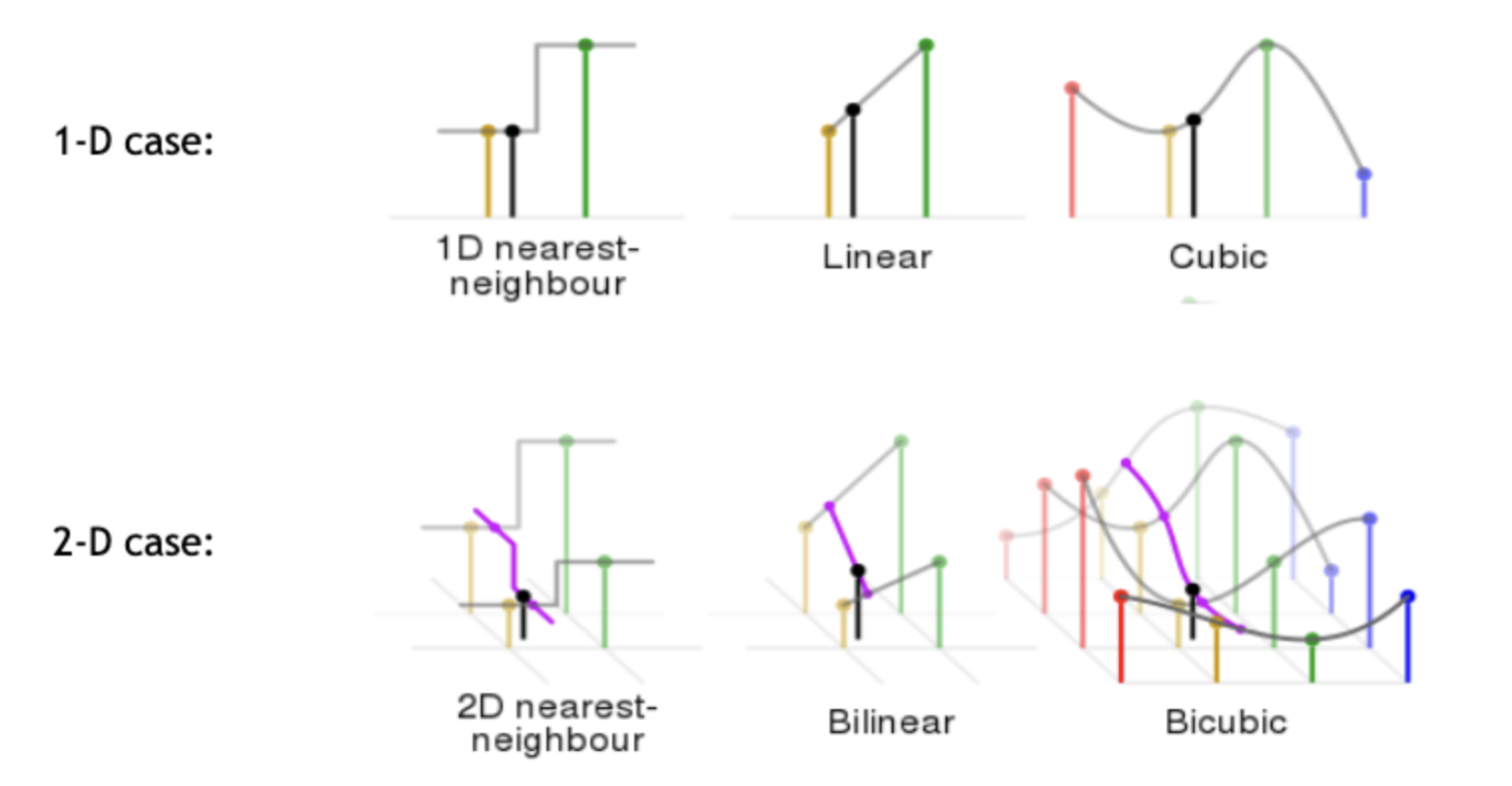
Nearest-Neighbor

제일 근처에 있는 값을 그대로 가져오는 방식이다.

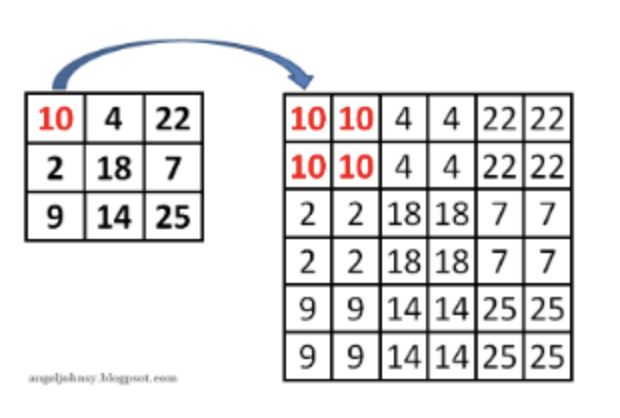
10이라는 값이 있으면 그 값을 Replicate하여 그대로 확장시킨다.

Linear

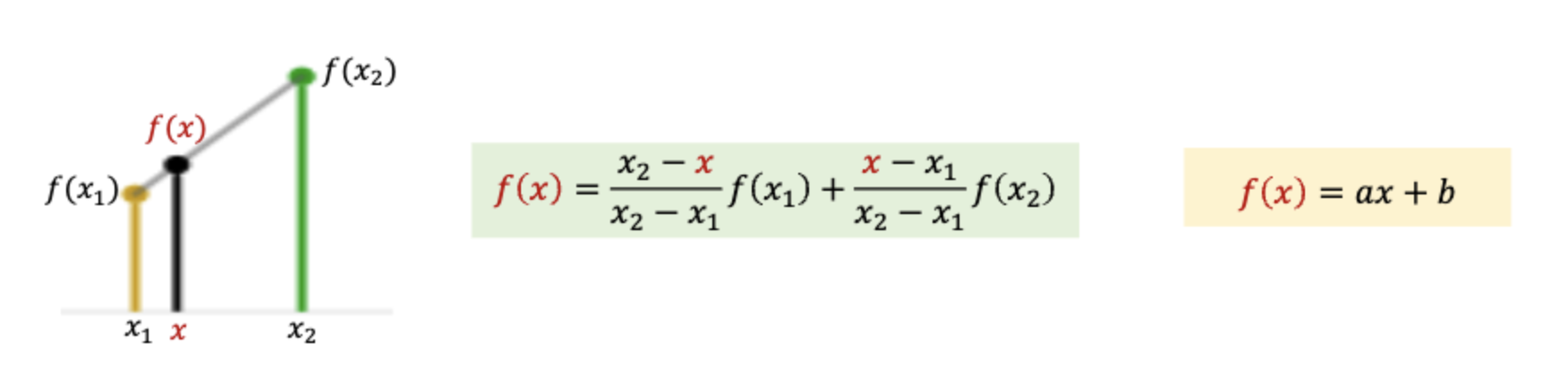
$f(x)=ax+b$라는 일차함수에 맞춰 $f(x)$의 값을 계산한다.

1차원에서는 Linear라고 부르며, 2차원은 y축이 하나 더 생긴 Bilinear라고 한다.



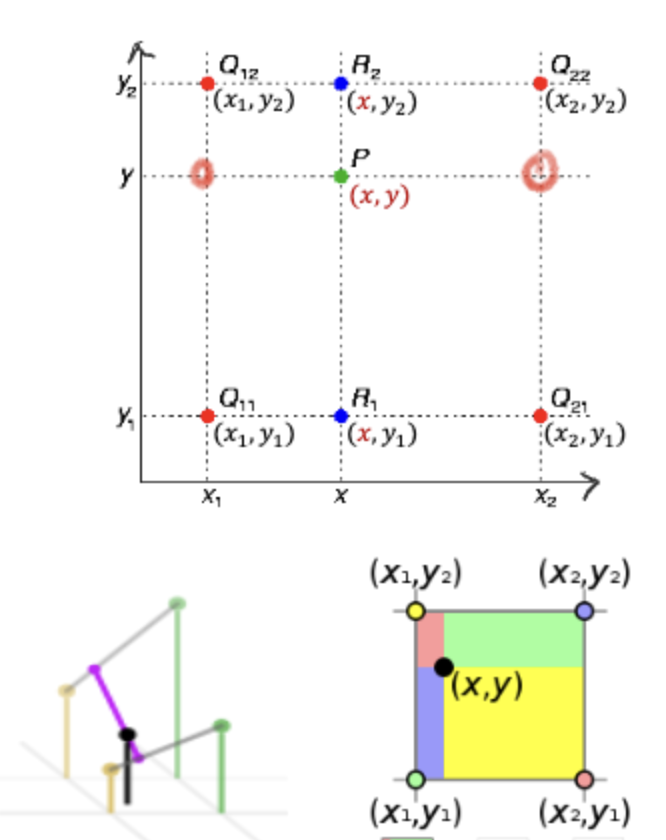
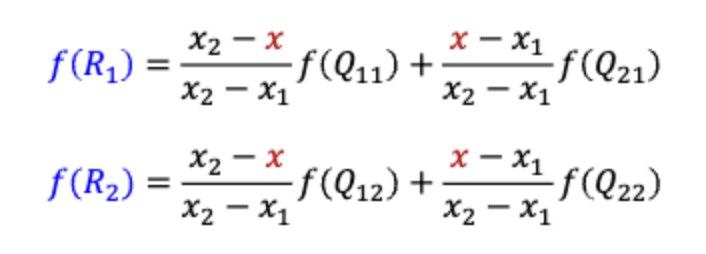
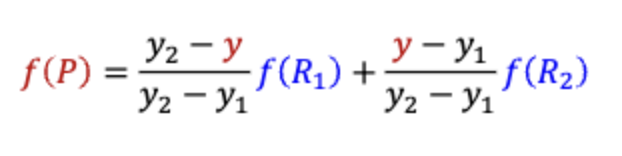
2차원에서는 이렇게 표현된다.

Cubic

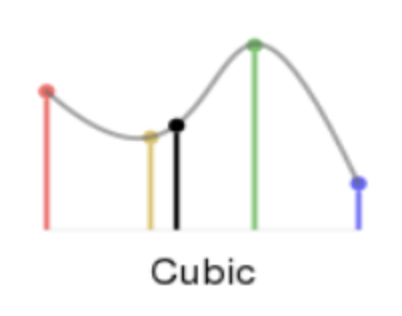
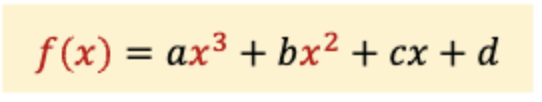
1차원에서는 곡선으로 표현된다. 점들을 여러개를 이어 다차함수에 대응되도록 구한다.

보통 점 2개를 이어 3차함수로 표현을 한다.

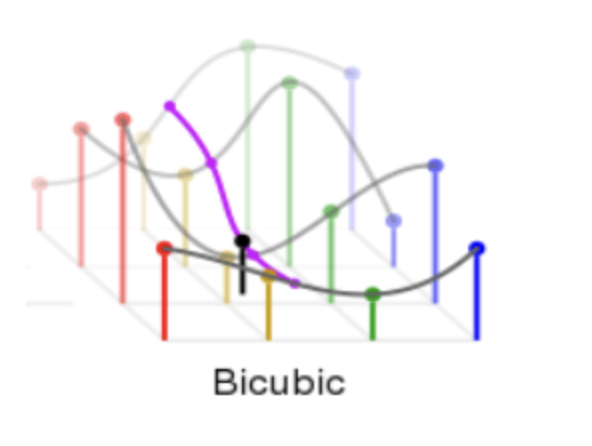
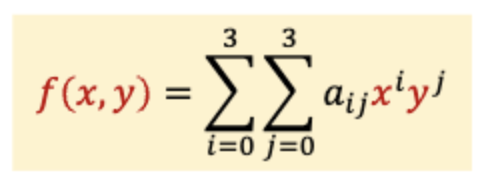
이를 2차원에서 표현하면 위와 같다.

Subsampling, Aliasing(Downsampling)

축소시키는 방법은 픽셀 중 특정 값을 선택하고 나머지는 버려야한다.

가장 간단한 논리로 이미지를 절반을 줄이고 싶다면 2x2의 픽셀을 평균값으로 지정하는 것일 수도 있다.

하지만, 이미지에서는 이 값이 절대 정확한 것이 아니다.

기존의 이미지 값이 [1, 1, 100, 100] 이 있는데 이를 평균을 내면 50.5가 나온다.

1과 100의 밝기 값이 있는데 이 방식을 사용하면 애초에 처음부터 없던 50이라는 밝기 값이 나오는 것이다.

그래서 Subsampling을 통해 실제로 원본 이미지에 존재하던 값을 선택해야한다.

위의 사진을 보면 (a)가 원본인데, 내가 말한 평균 값 필터로 진행하면 (c)처럼 빵떡같은 이미지가 나오는 것이다.

(b)의 방법은 아까 배운 Interpolation을 적용한 것인데 이 방식을 적용하면 Aliasing이 생긴다.

Shannon Sampling Theorem

공돌이의 수학 노트 여기서 잘 정리되어있다.

샘플링의 진동수 $f_s$는 신호의 최대 진동수 $f_{max}$의 2배보다 크면 원래의 신호를 알 수 있다는 말이다.

2배보다 작으면 샘플링이 덜 되어서 다른 신호로 착각할 수 있다.

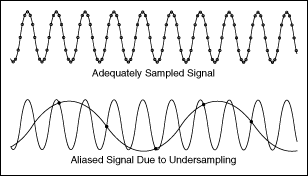
위의 이미지를 보면 위의 신호에서는 샘플링의 주기가 굉장히 짧다. 즉, $f_s$가 크다는 말이다. 이때는 원래 신호를 예측할 수 있다.

하지만 아래의 경우, 샘플링의 주기를 길게 가져가 $f_s$가 $2f_{max}$보다 작다면, 저렇게 널널한 신호로 예측할 수도 있다.

Aliasing의 이유

얼라이싱이라고도 한다. 보통 이미지를 축소하면 계단현상이 발생하는 것이다.

휴대폰으로 옛날 모니터 화면을 찍거나, 게임할때 안티얼라이싱 옵션을 키지 않거나 할때 발생한다.

이런 계단처럼 꺾여보이거나 위의 정강이 부분처럼 줄무늬 모양이 생기는 현상을 줄여주는 방식이다.

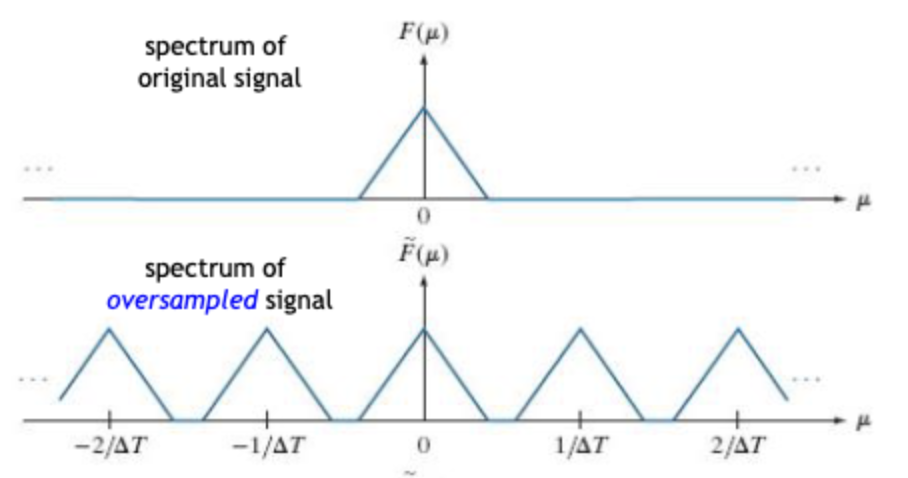
위의 기존 신호를 샘플링하면 Frequency Domain에서 Periodic Repetition을 띄게 된다.

근데 $f_s<2f_{max}$가 되면 저 주기성을 띄는 피라미드가 겹쳐진다.

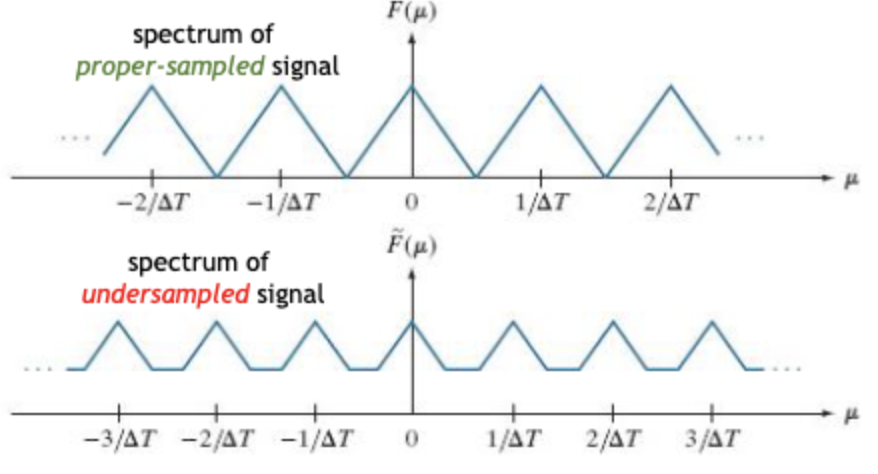
이때 마지막 아래의 경우가 바로 Aliasing이 일어나는 것이다.

원본의 신호를 잃고 다른 신호로 해석되기 때문이다.