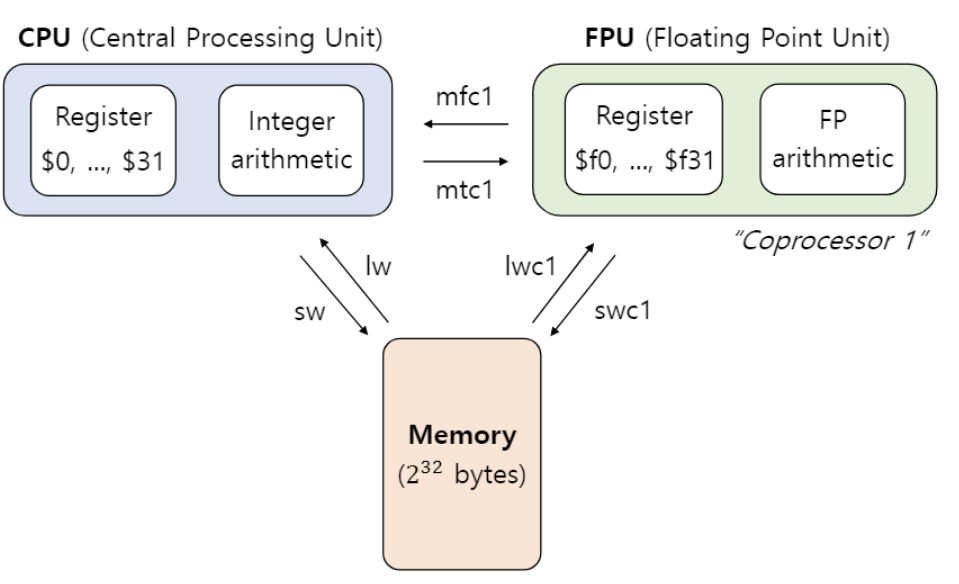
Floating point
- 컴퓨터에 실수를 저장하는 방법
- 부동(움직이지 않는다가 아니라, flying moving, 둥둥 떠다닌다는 의미) 소수점 표현
Term
Normalization
- 소수점을 표현할때 (10진수기준) 식으로 표현하는 방식
- 1의 자리수는 0이 되면 안됨
- Normalized:
- Not normalized:
- 2진수는 0과 1이므로 1의 자리수가 0이 되면 안되므로 무조건 1이옴
- Binary Normalized: 이 고정
Single precision

- Sign bit: 0이면 양수, 1이면 음수
- Exponent bit: 에서 n에 해당
- fraction bit: 에서 ○○○○에 해당
- s: 1 / e: 8 / f: 23 외우자! / 다합치면 32bit = 1word = 1개의 레지스터 사용
Double precision

- Sign bit: 0이면 양수, 1이면 음수
- Exponent bit: 에서 n에 해당
- fraction bit: 에서 ○○○○에 해당
- s: 1 / e: 11 / f: 52 외우자! / 다합치면 64bit = 2word = 2개의 레지스터 사용
IEEE 754 Standard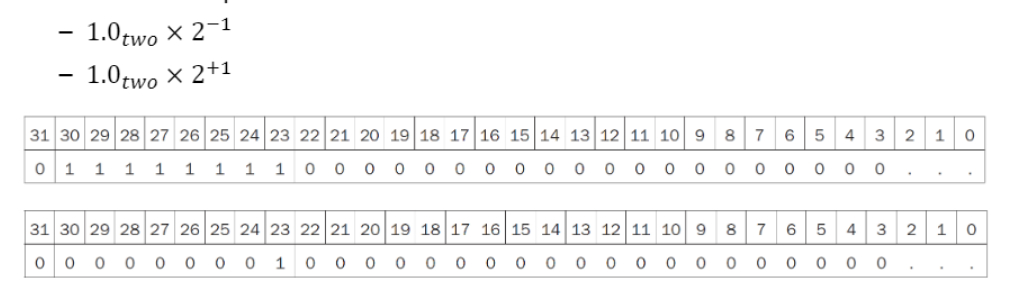
- 에서 로 표현
Biased notation
- Exponent 8bit는 sign number라 -1과 1을 눈으로 볼땐 -1이 11111111로 더 커보임
- 그래서 bias를 두어 Exp - Bias로 평행이동시켜 이 오해를 해결
- Single Precision: 127 / Double Precision: 1023
Representation
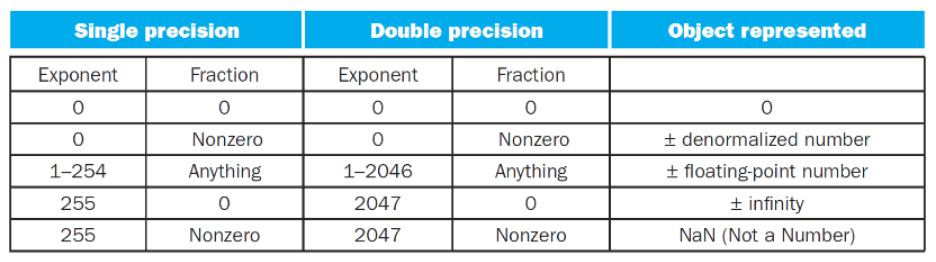
- E=0, F=0, 매우작은수
- E=0, F≠0,
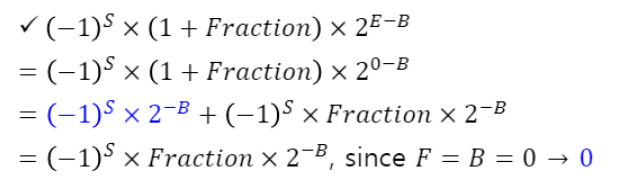 파란색 -B는 어차피 0이므로 생략 -> 결론적으로 -B는 1의 자리가 1이 아니므로 Not normalized
파란색 -B는 어차피 0이므로 생략 -> 결론적으로 -B는 1의 자리가 1이 아니므로 Not normalized - E=000....1~111~1110, F=Anything, 우리가 일반적으로 배운 부동소수
- E=11...1, F=0, 128은 무한대로 발산
- E=11...1, F≠0, 128
Example
Q. 1100/0000/1010/0000/0000/0000/0000/0000을 소수로 나타내면?
A. 1/10000001/0100000000000000000000000000이므로
129-127=-1.125×4=-5.0
Addition
- 큰 지수에 맞춰 통일
- 두개의 유효숫자(significand)를 더함
- normalization을 위해 일의 자리 수를 1로 맞춤
- 유효숫자 자리수만큼 반올림
Example(4개의 significand, 2개의 exponent라고가정)
0.011 × 21 + 1.101 × 2-1? (십진수로는 0.75 + 0.8125 = 1.5625)
1. 큰 지수인 2에 맞춰 1.101 × 2-1를 0.01101 × 21?
2. 0.011와 0.01101을 더해 0.11001× 21
3. normalization을 해서 1.1001×20
4. 1.1001에서 유효숫자수에 맞춰 반올림해서 1.101×21가 된다
Multiplication
- 결과값의 지수를 계산
- 유효숫자(significand)를 더함
- normalization을 위해 일의 자리 수를 1로 맞춤
- 유효숫자만큼 반올림
- 부호검증
Example(4개의 significand, 2개의 exponent라고가정)
0.011 × 21 × 1.101 × 2-1? (0.75 × 0.8125 = 0.609375)
1. 두 지수는 1과 -1이므로 합은 0
2. 0.011 × 1.101 = 0.100111이므로 0.100111 × 20
3. normalization을 해서 1.00111 × 2-1
4. 유효숫자에 맞춰서 반올림해서 1.010 × 2-1
5. 원래 양수였으므로 최종적으로 +1.010 × 2-1
MIPS Instruction
Register
- Floating point를 위한 레지스터 $f0~$f31까지 존재
- single precision, double pecision을 구분하기 때문에 2개의 레지스터가 쌍으로 연결
- f1을 하나의 소수를 저장하는 공간으로 보면됨. 만약 single precision이라면 $f0만 쓰는꼴
Instruction
- R, I, J Format처럼 floating point를 위한 FR, FI Format이 존재
Example
float f2c (float fahr)
{
return ((5.0/9.0) * (fahr - 32.0));
}- Register allocation: fahr -> $f12 (floating point는 $a에 저장안하고 모두 $f에 저장)
- Code (float은 immediate, unsigned가 없기때문에 메모리에서 lwc1 const($gp)로 가져와야함)
f2c:
lwc1 $f16, const5($gp) # $f16 = 5.0
lwc1 $f18, const9($gp) # $f18 = 9.0
div.s $f16, $f16, $f18 # f16 = 5.0 / 9.0
lwc1 $18, const32($gp) # $f18 = 32.0
sub.s $f18, $f12, $f18 # $f18 = fahr - 32.0
mul.s $f0, $f16, $f18 # $f0 = (5.0/9.0)*(fahr-32.0)
jr $jaDGEMM
- 3232 실수가 저장된 행렬 3개를 C = C + A B 계산하는 성능측정 모델
void mm (double c[][], double a[][], double b[][])
{
int i, j, k;
for (i = 0; i != 32; i++)
for (j = 0; j != 32; j++)
for (k = 0; k != 32; k++)
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}- HINT: Load Immediate(li), Load Double(l.d), Store Double(s.d)
- HINT: 다차원 배열은 1차원 배열로 쭉 펴서 접근하는 방식으로 생각하면 편함
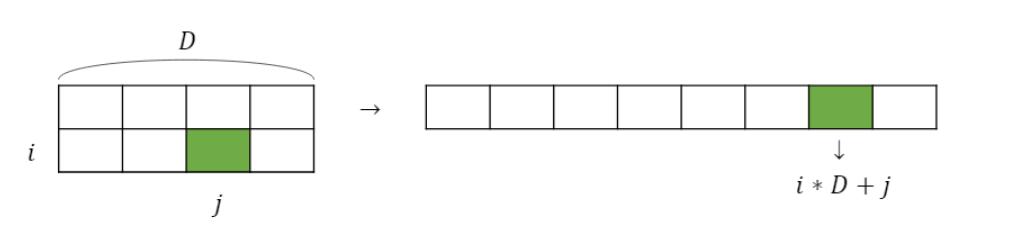
- Register allocation: c $a0, a $a1, b $a2, i $s0, j $s1, k $s2
mm:
li $t1, 32
li $s0, 0
L1: li $s1, 0
L2: li $s2, 0
sll $t2, $s0, 5 # $t2 = i * D = i * 32
addu $t2, $t2, $s1 # $t2 = i * D + j
sll $t2, $t2, 3 # $t2 = byte offset of [i][j]
addu $t2, $a0, $t2 # $t2 = byte address of c[i][j]
l.d $f4, 0($t2) # $f4에 c[i][j]의 double floating point 저장
L3: sll $t0, $s0, 5
addu $t0, $t0, $s2
sll $t0, $t0, 3
addu $t0, $t0, $a1
l.d $f16, 0($t)
ssl $t0, $s2, 5
addu $t0, $t0, $s1
ssl $t0, $t0, 3
addu $t0, $t0, $a2
l.d $f18, 0($t0)
mul.d $f16, $f16, $f18
add.d $f4, $f4, $f16
addiu $s2, $s2, 1
bne $s2, $t1, L3
s.d $f4 0($t2)
addiu $s1, $s1, 1
bne $s1, $t1, L2
addiu $s0, $s0, 1
bne #s0, $t1, L1Accurate Arithmetic
- Floating point는 크기가 제한되어 있기때문에 예측값일 뿐 double precision기준 최대 52bit
- 그래서 Guard, Round비트 두개를 두어 계산
with guard and round bits
- Align the exponent from 1.01 × 20 -> 0.0101 × 22, 0.01 × 22
- Add the significand 0.0101 + 0.01 = 0.1001이다
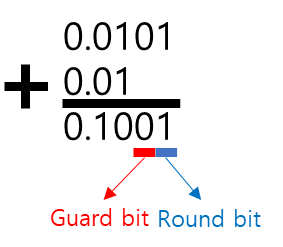 Guard, Round bit를 두어 기존의 significant 2비트를 위해 Round를 처리
Guard, Round bit를 두어 기존의 significant 2비트를 위해 Round를 처리
Float Instruction with memory