Intensity Transformations
Transformation하면 컴퓨터그래픽스에서 배운 정사영, 평행이동, 회전 이런게 생각날 것이다.
영상처리에서는 밝기를 변화를 많이 시킨다.
애초에 이미지를 [세로][가로][채널]의 값을 Intensity로 저장하니까 말이다.
이러한 밝기를 조절하면 어둡게 밝게 할 수 있을 뿐만 아니라, 블러처리를 하거나 선명하게 하거나를 할 수 있다.
경계선을 찾아 경계를 더 밝게하면 선명해질 것이고, 경계를 어둡게하면 흐릿해질 것이니 말이다.
Definition
Spatial Domain Processing
이미지가 차지하는 그 면적을 가공하는 그 행위를 뜻한다.
식은 다음 처럼 나타낸다. g(x, y)결과 이미지, f(x, y)입력 이미지, TSpatial Domain Processing이다.
Intensity Transformation
위는 이미지 자체를 통째로 바꾸는 그 과정을 뜻했다면 여기는 작은 픽셀의 값을 바꾸는 느낌이 강하다.
로 표현하며, s결과 밝기, r입력 밝기, T변환 함수이다.
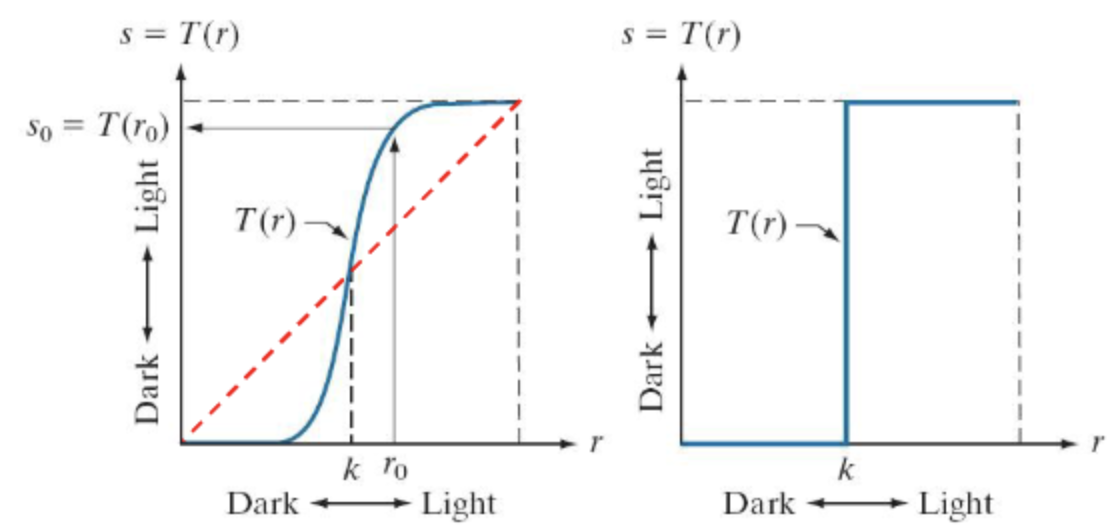
- 왼쪽이미지는 k보다 어두운 밝기는 더 어둡게, 밝은 밝기는 더 밝게 변환한다.
결과적으로는 이미지의 대비가 강조되는 효과를 얻는다. - 오른쪽이미지는 Threshold(임계치) k보다 낮으면 모두 땡처리, 나머지는 최대로 만든다.
결과적으로는 이미지가 흑백 2가지로만 나뉘며 경계를 확실히 구분할 수 있게 된다.
Saturate
이미지를 전체적으로 밝게 혹은 어둡게 하고 싶으면 어떻게 해야할까?
이미 밝기가 255인 픽셀이 있는데 더 밝게는 못할 것이다.
이러한 max값과 min값을 잘 정의해서 이부분은 그대로 놔두어야한다.
이를 Saturate라고 많이 표현하며 다음의 함수를 따른다.
Basic Intensity Transformation Functions
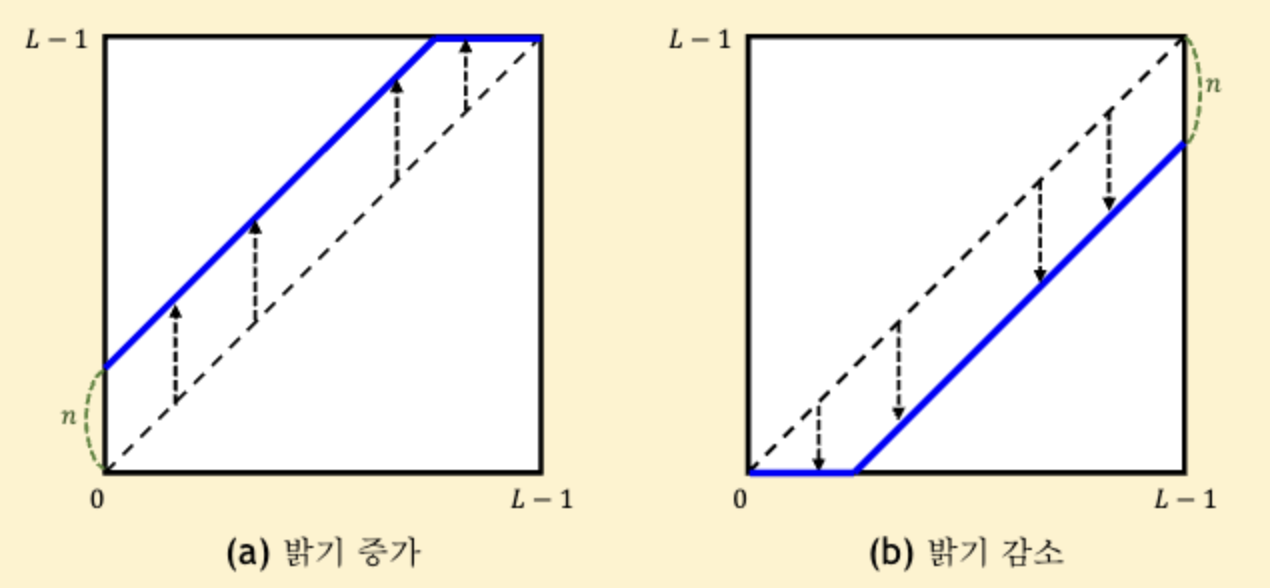
밝기를 변환하는 함수는 크게 4가지정도로 구분할 수 있다.
1. Image Negatives
밝기를 반전하는 것이다.
가 Identity Function이라면 반대는 무엇일까? ?
아니다. 정확히는 절편을 올려줘서 일 것이다.
즉, 로 표현할 수 있다.
2. Log Transformations
로그함수를 밝기 변환 함수에 쓰는 것이다.
로 사용한다.
값은 입력 밝기가 일 때, 결과 밝기도 이 되도록 잘 조절해야한다.
3. Power-Law Transformations
제곱함수를 사용하므로 아래의 꼴로 나타낸다.
로, 는 에 맞춰주는 역할, 는 제곱의 정도로 잘 조절해야한다.
가 0에 가까워질수록 ┌모양에 가까워지며, 커질수록 ┘ 모양이다.
여담으로 옛날 CRT 디스플레이는 2.5감마만큼 어둡게하는 특성이 있어서,
마지막 송출에서 1/2.5 감마만큼 밝게 처리하는 기법을 사용하였다.
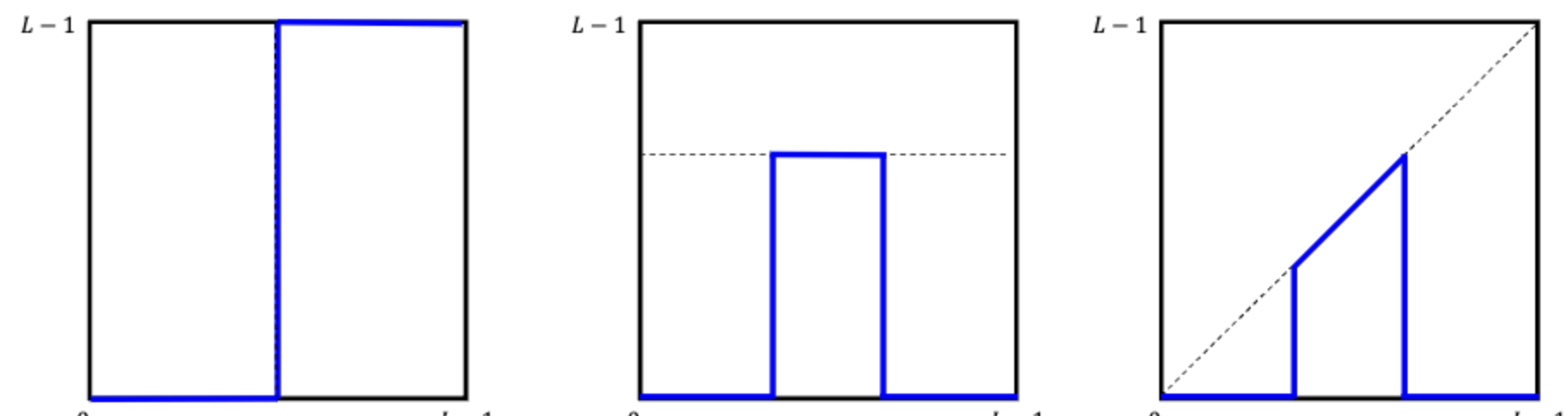
4. Piecewise-Linear Transformations
조각을 내어 마음대로 커스터마이징한 변환이다.
Linear하므로 절대 곡선이 아니라, 선들의 연속으로 이루어져있다.
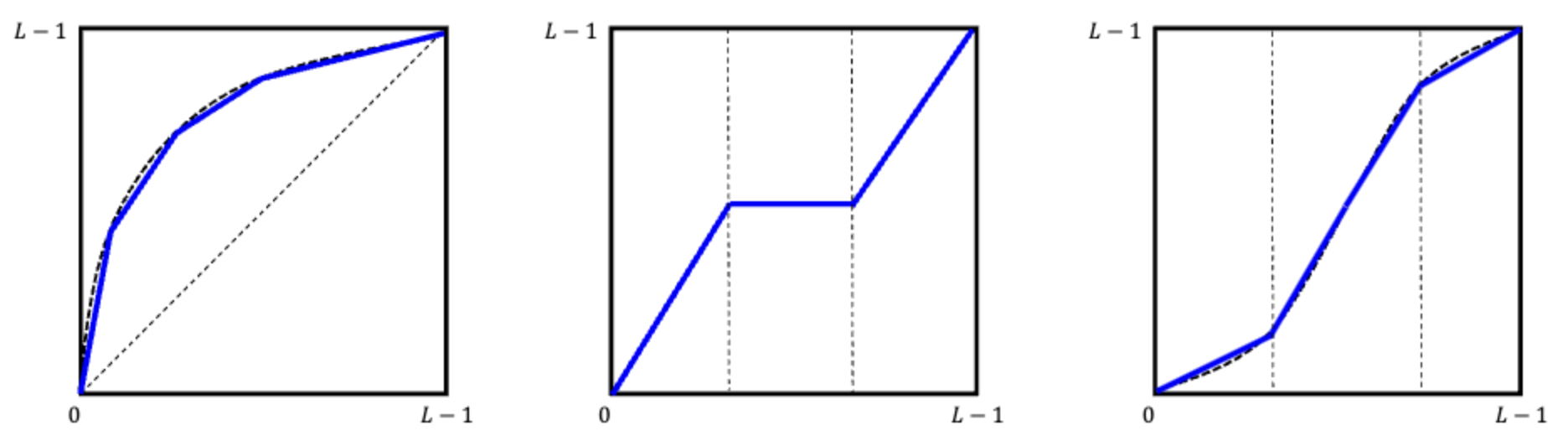
Monotonic Increasing
단조증가 함수를 뜻하며, 그래프가 점점 증가하는 형태를 띄어야한다.
미분한 결과가 기울기는 반드시 0이상이어야하는 것이다.
변환 함수들은 Monotonic Increasing 형태가 되어야 Data Loss없는 변환을 할 수 있다.
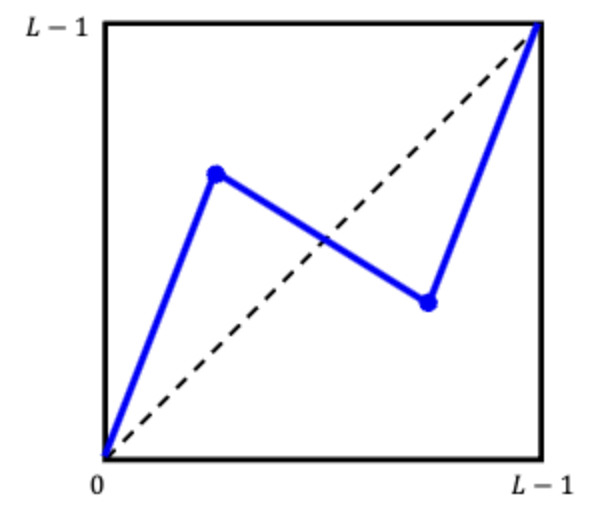
위와 같은 변환함수라면, 결과 밝기로 가는 입력 밝기는 3가지가 되어버린다.
이러면 최초의 이미지는 어떤 밝기 값을 가졌는지 역으로 추론하기가 어렵다.
- Monotonic increasing function
- Strictly(엄격한) monotonic increasing function
Histogram Equalization
밝기들을 히스토그램으로 ~ 단계를 나눠 그릴 수 있을 것이다.
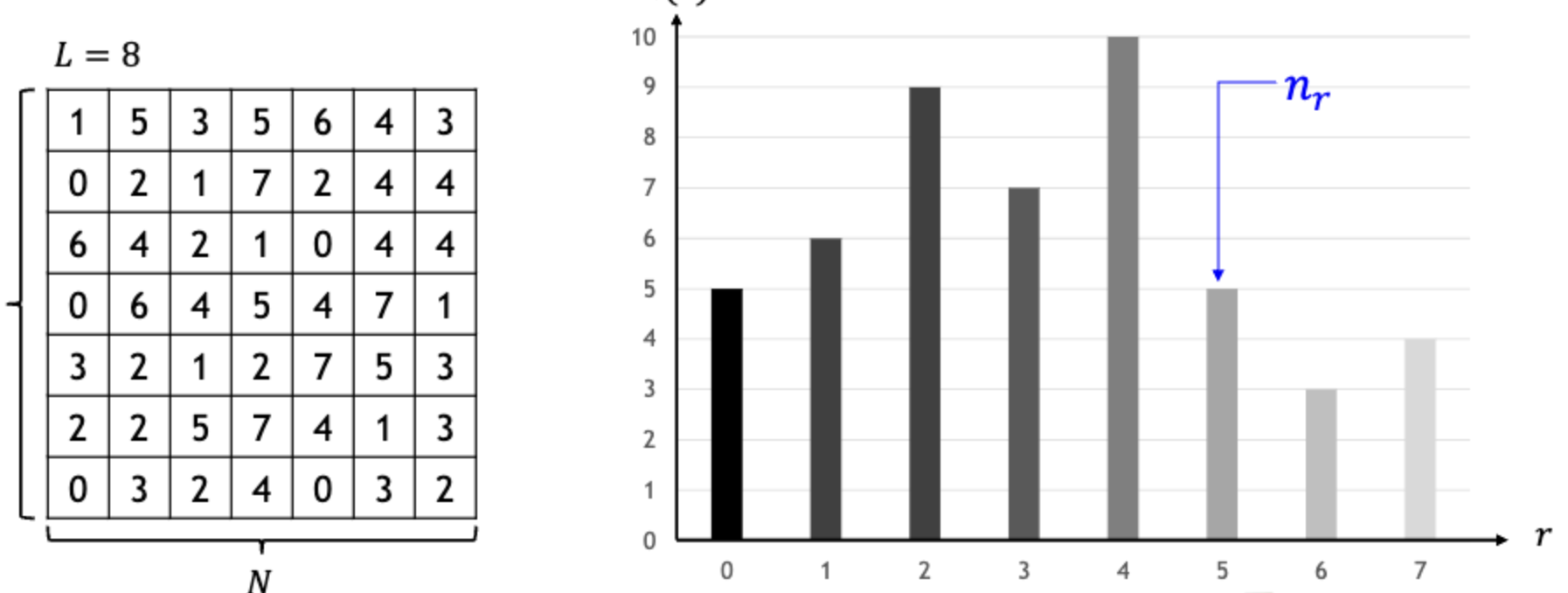
이 히스토그램은 보통 정규화(Normalization)을 하여 다음처럼 나타낸다.
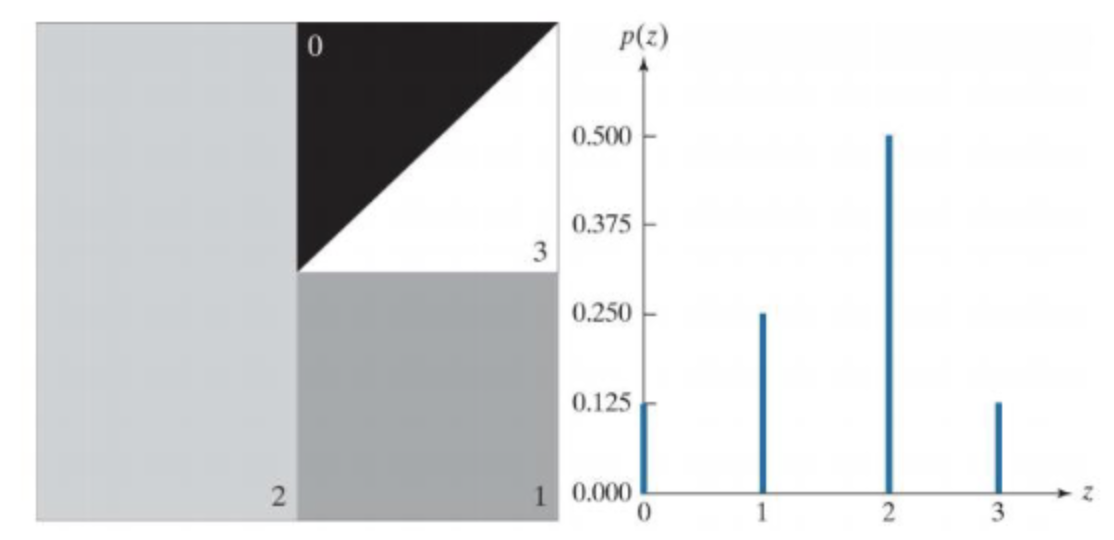
참고로 는 세로픽셀개수와 가로픽셀개수의 곱이다.
Histogram, Probability
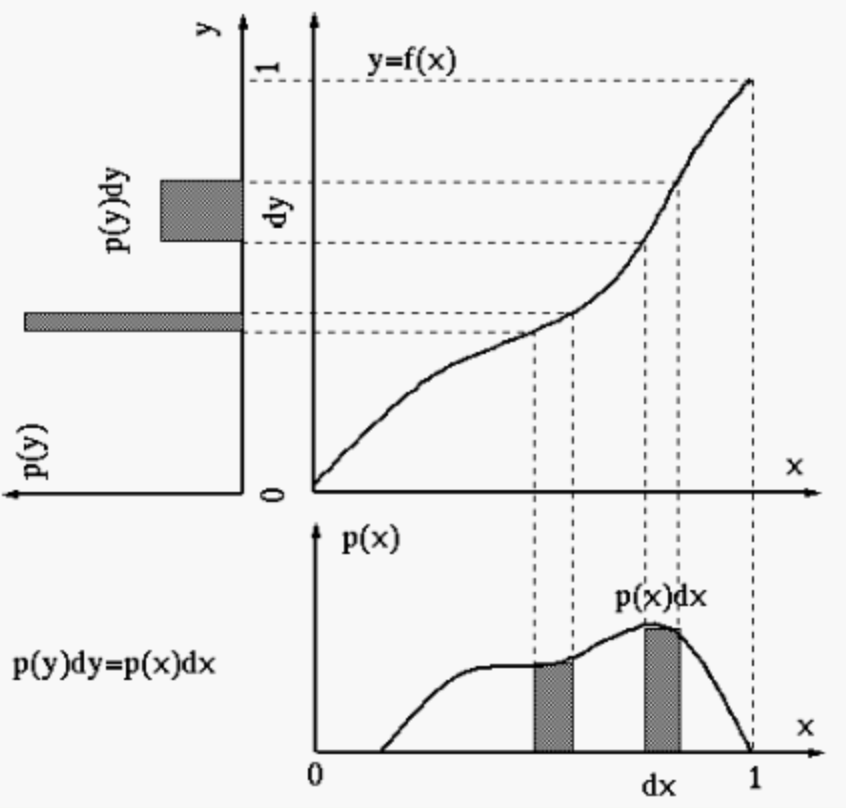
또한 히스토그램은 정규화를 진행하였다면 확률밀도함수(PDF)라고도 생각할 수 있다.
부터 까지의 총합은 1인 확률들에 대한 함수이기 때문이다.
위의 사진에서는 와 에 대한 함수, 와 에 대한 함수가 PDF이자 히스토그램이라 볼 수 있다.
여기서 를 만족한다. 확률의 합은 항상 같을 것이니까.
PDF인 x에 대한 함수를 CDF인 y=f(x)라는 함수를 거쳐 y에 대한 PDF로 변환되는데,
이는 마치 Intensity Transformation같아 보인다.
그래서 히스토그램을 새로운 히스토그램으로 변환하는 함수는 누적분포함수(CDF)라고 생각할 수 있다.
이러한 히스토그램을 쫙 펴서 한곳에 몰린 Intensity가 없도록 하는 것이 Histogram Equalization이다.
밝기가 고르게 분포해야 사람이 인식하기 편한 이미지가 되기 때문이다.
Principal
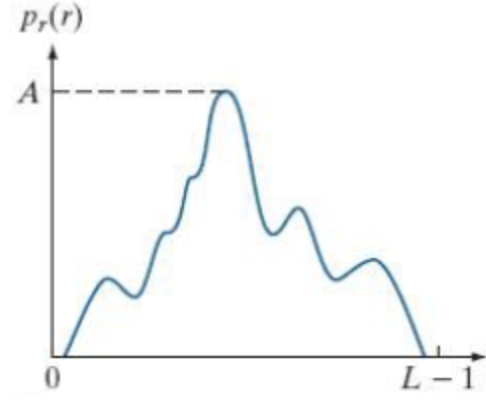
한곳에 밝기가 치우친 이미지를
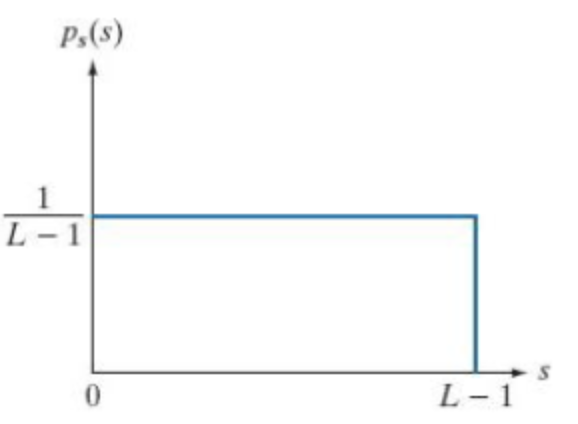
여러가지 밝기의 이미지가 고르게 펴지도록 하는 을 찾아야한다.
아까 CDF를 통해 x와 y에 대한 함수로 구했던 식을 가져오자.
그런데 를 모두 평활화하여 에 근접하는게 목표이므로 을 대입한다.
이 된다. 여기에 양변을 적분을 하여 CDF꼴로 바꾼다.
이 된다. 양변에 을 곱해준다.
즉, 히스토그램을 적분하면 Intensity Transform Function이 되는 것이다.
하지만 적분은 Continious에서만 쓰고, 실제 이미지는 Discrete하여 다음식으로 표현한다.
Example
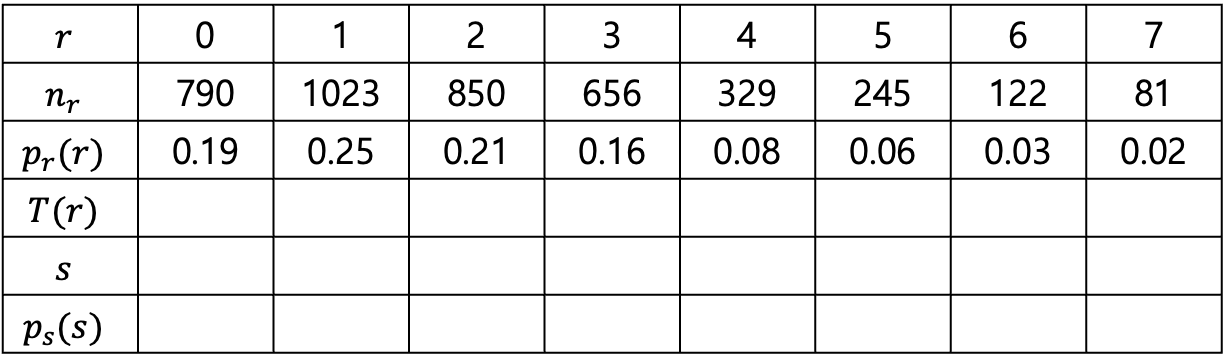
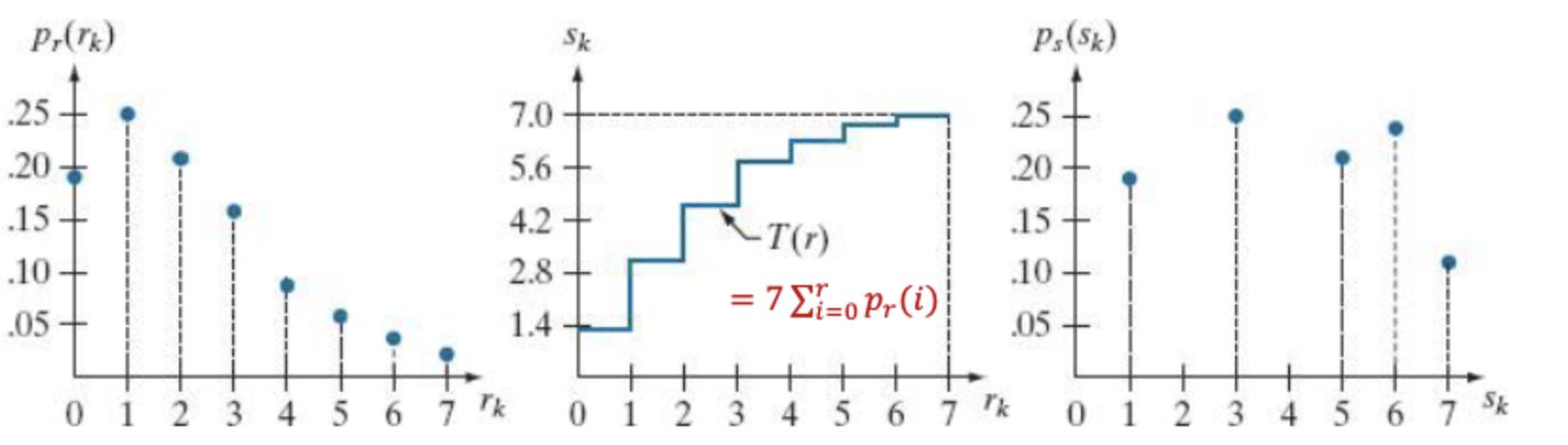
다음의 히스토그램이 있다면 다음의 식으로 빈칸을 채워나갈 수 있다.
여기서 은 8이되겠다.
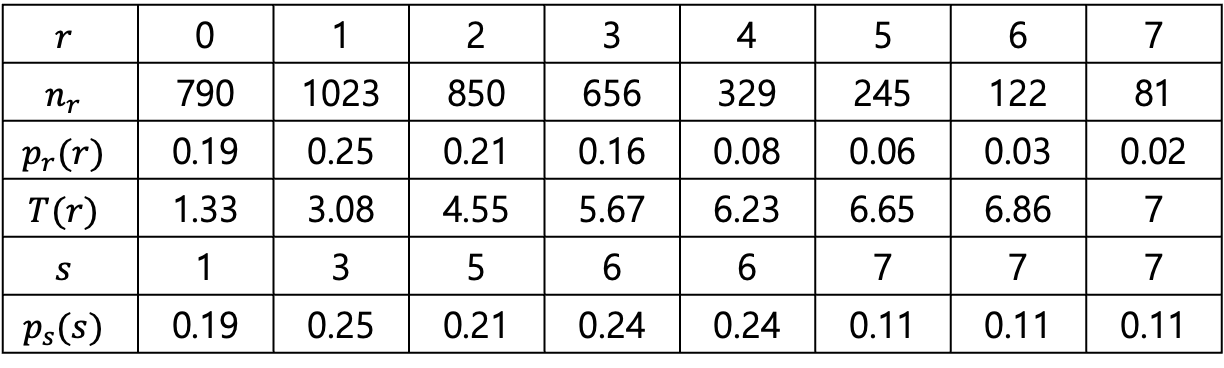
는 변환된 s에 대한 히스토그램을 다시 정규화해서 그리면 된다.
r(원래 밝기) 0에서 s(변환된 밝기)1로 전체픽셀의 0.19만큼 바뀌었으므로
r(원래 밝기) 1에서 s(변환된 밝기)3로 전체픽셀의 0.25만큼 바뀌었으므로
r(원래 밝기) 2에서 s(변환된 밝기)5로 전체픽셀의 0.21만큼 바뀌었으므로
r(원래 밝기) 3, 4에서 s(변환된 밝기)6로 전체픽셀의 0.16+0.08만큼 바뀌었으므로
이런식으로 적으면 위의 표를 채울 수 있다.
P.S. Histogram Stretch
히스토그램의 값의 분포가 바뀌는 것이 아니라 가로로 늘어나는 느낌이다.
으로 는 가장 밝은 밝기, 은 가장 어두운 밝기
Histogram Matching
원하는 임의의 분포로 히스토그램을 변환하고 싶을 때가 있을 것이다.
우리는 히스토그램을 평활화하는 방법을 배웠기에 이를 응용해서 원하는 분포로 만들 수 있다.
원하는 분포를 원본 분포를 , 히스토그램으로 펴진 Uniform을 라고 하,
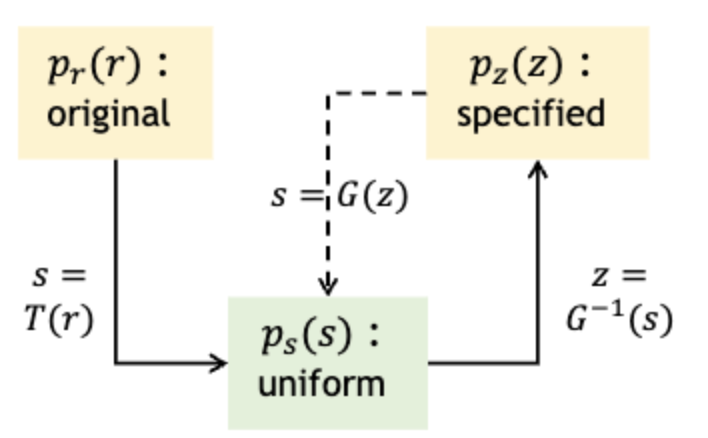
원하는 분포를 평활화하는 변환 의 역함수를 구해 을 로 바꿀 수 있다.
