Meshing
물체를 모델화하려면 Vertex들을 이어서 Polygon을 만들어야한다.
이 Polygon은 그물망(Mesh)처럼 보이기도 한다.
물체를 그물망처럼 변환하는 과정을 Meshing이라고 한다.
이 원리를 살펴보자.
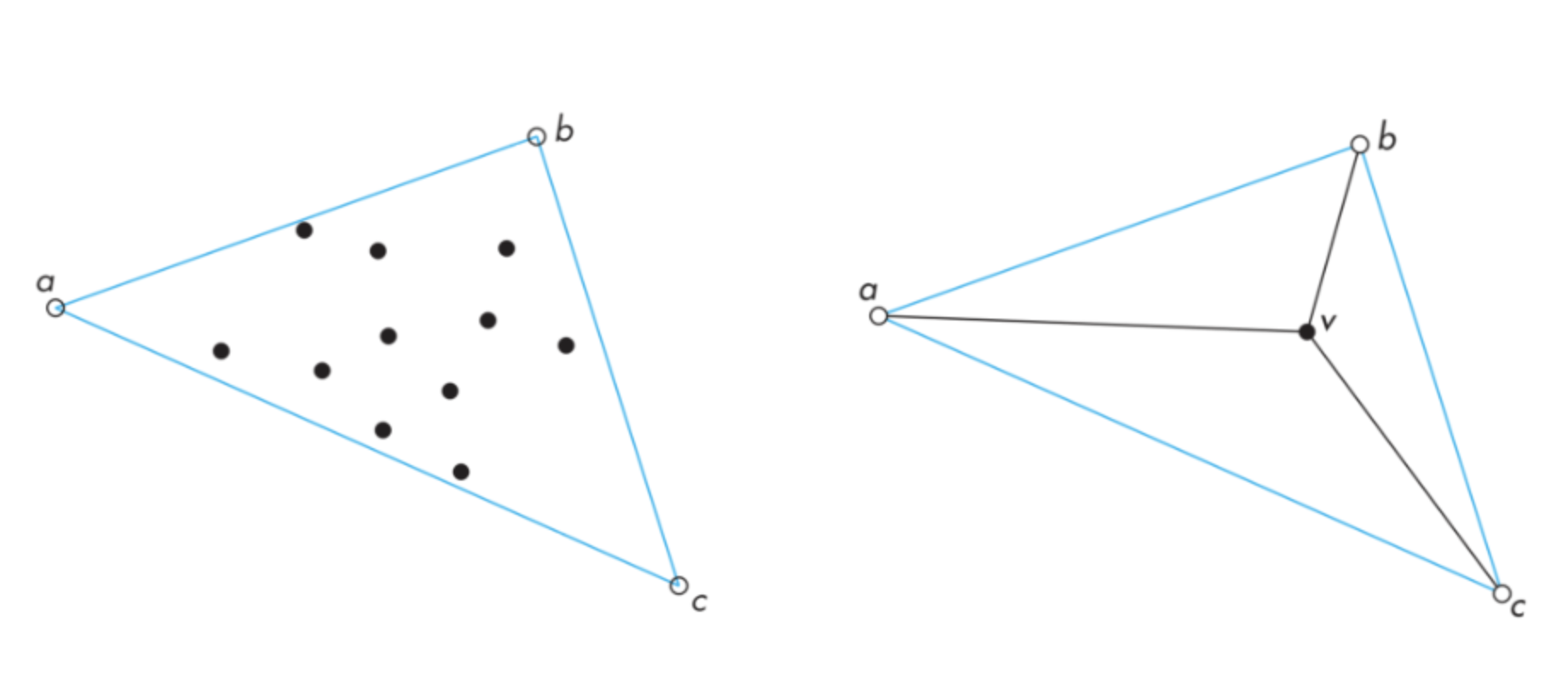
Delaunay triangluation
물체를 삼각형들의 모음으로 만들 수 있는 알고리즘이다.
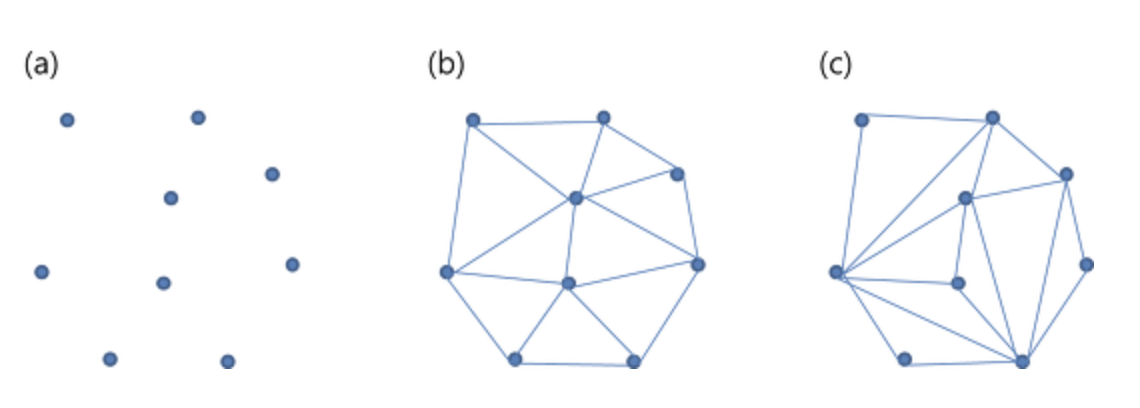
b사진은 안정적인 폴리곤처럼 보이고, c는 너무 각들이 둔각이 나온다.
최대한 둔각이 나오지 않도록 모든 각이 예각이도록 선택하는 기술이다.
Subdivision
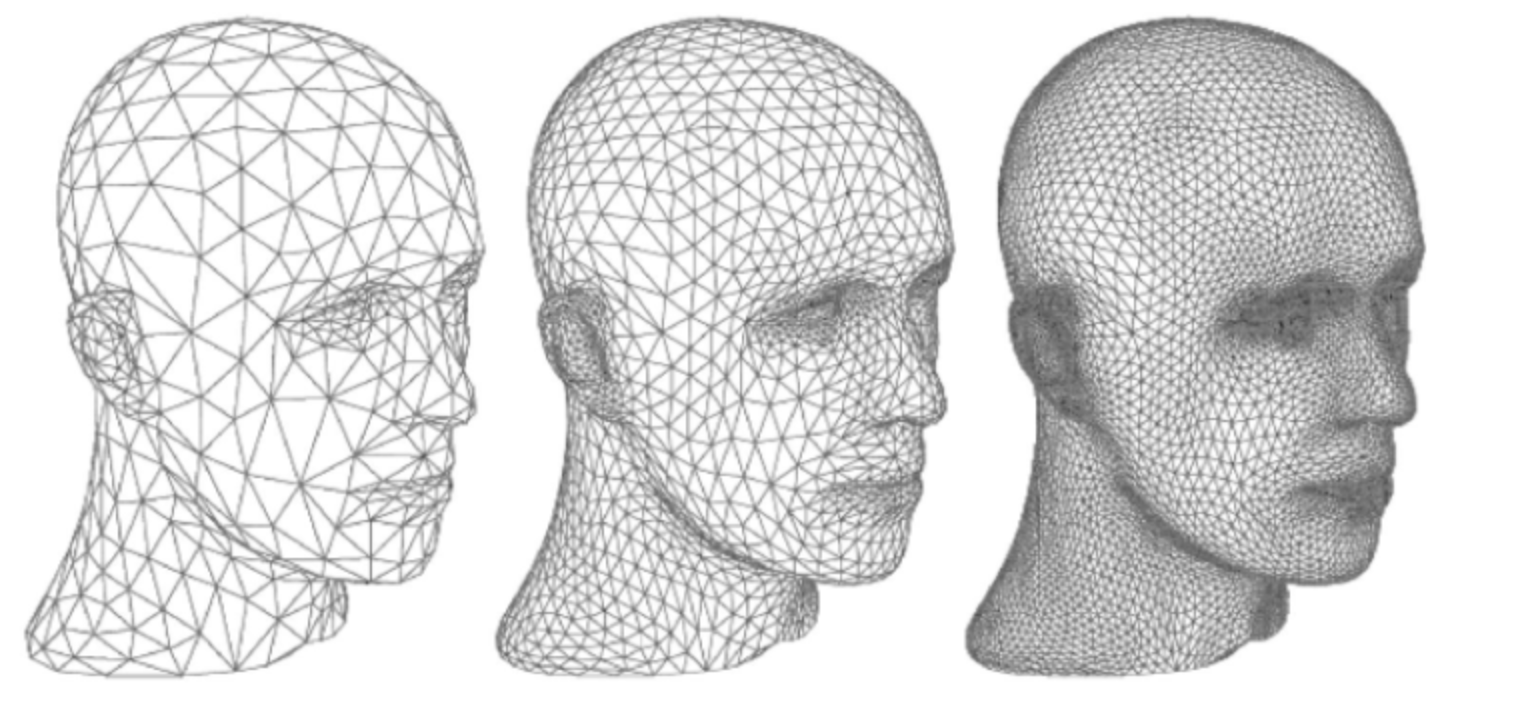
널널하게 만든 폴리곤을 촘촘한 모델로 점점 나아가는 기술이다.
원리는 다음과 같다.
Subdivision Curves
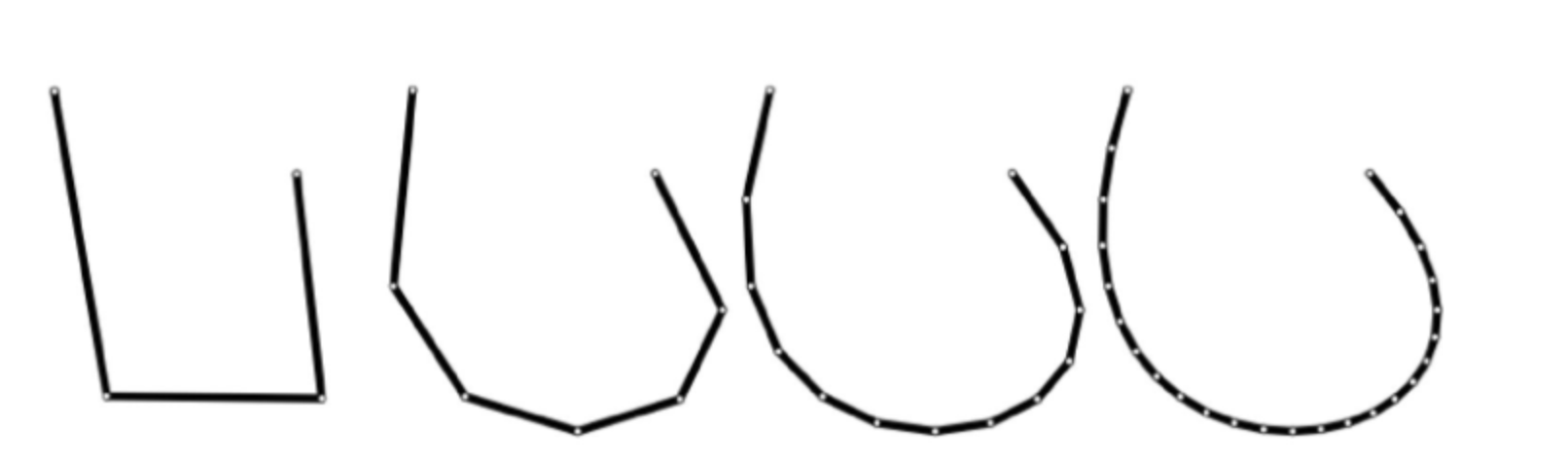
Vertex사이에 점을 찍어서 좀더 굴곡지게 움직여주는 것이다.
이 곡선을 Subdivision Curves라고 한다.
계속 나아가면 거의 곡선에 근접하도록 변환한다.
그래서 적당한 단계를 잡고 진행해야하며, 너무 많이 진행하면, 구에 가까운 형태의 모델이 되어버린다.
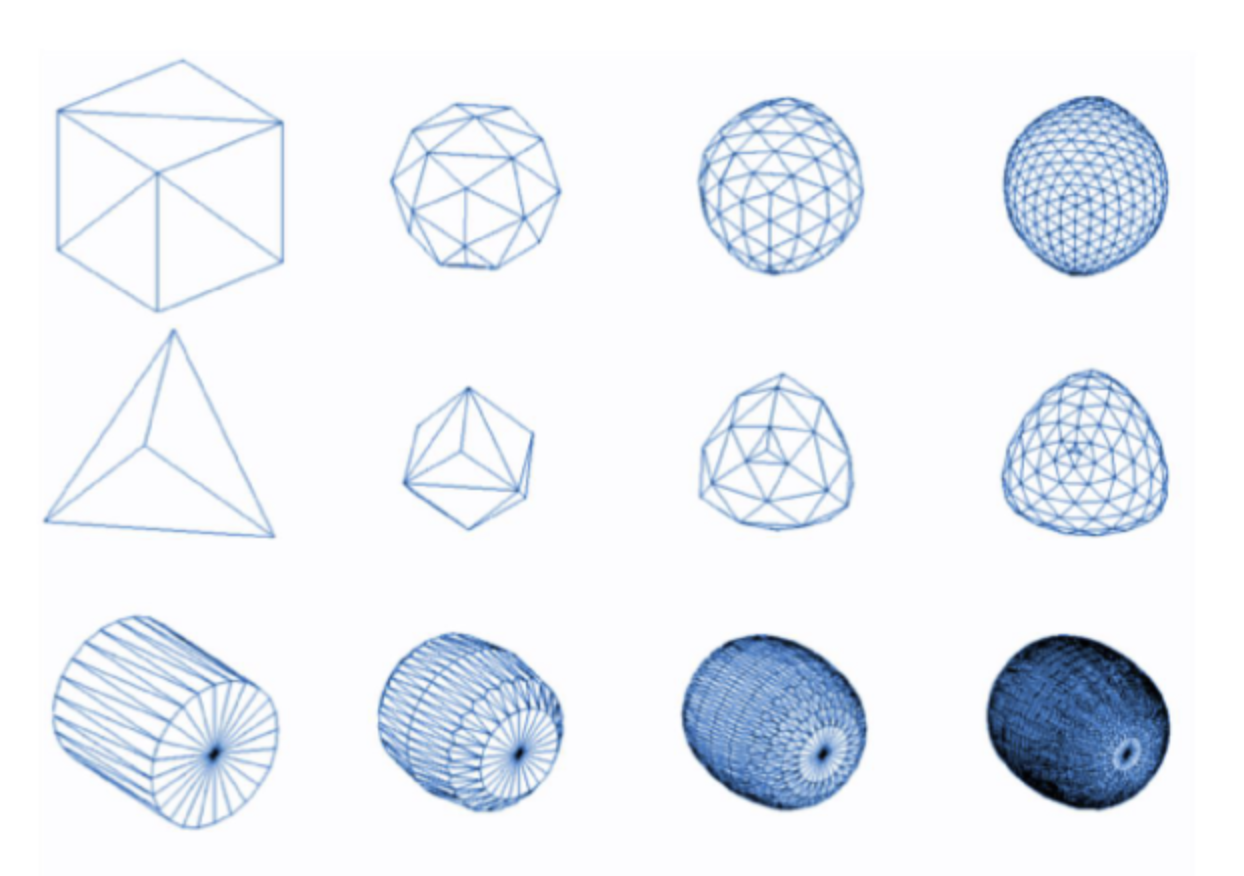
Move the vertices
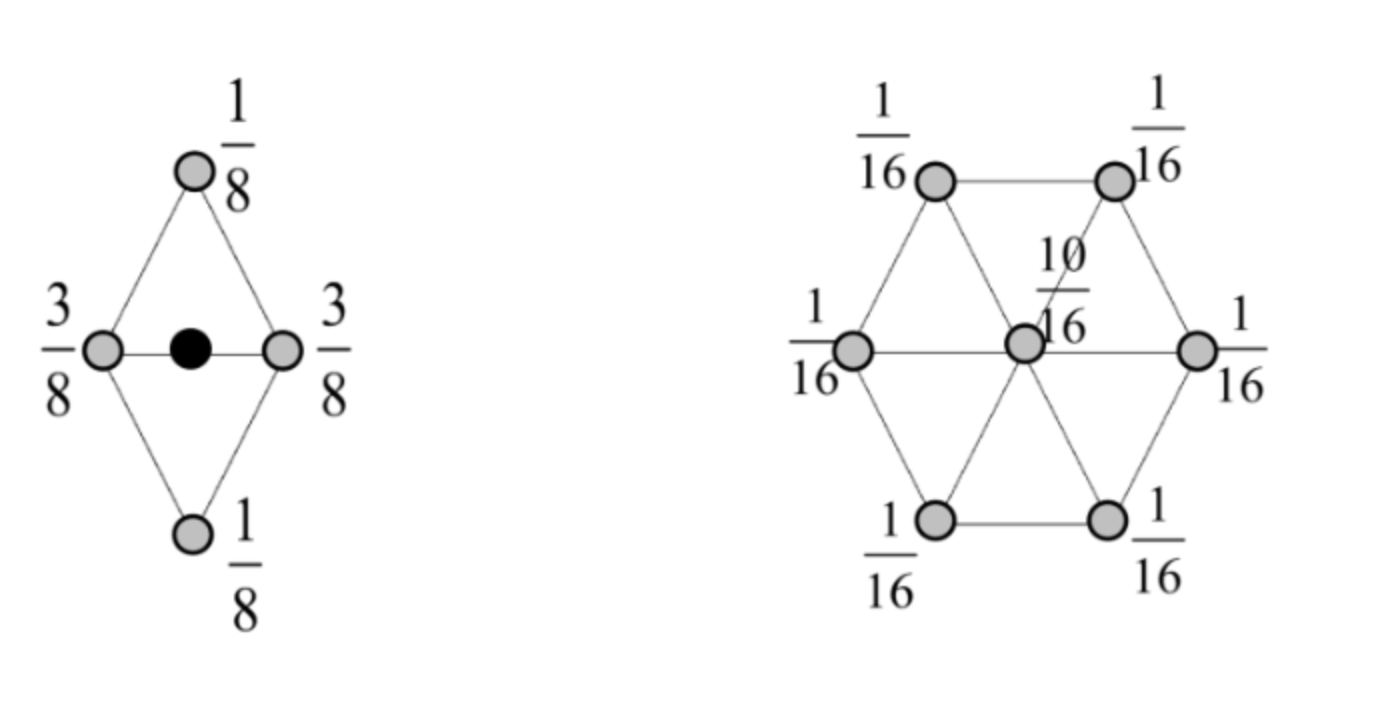
Subdivision을 위해 점을 찍을때 어디에 찍을지 정해야한다.
각 점들의 가중치들을 매겨 찍을 수 있다.
가중치를 비대칭적으로 하면, 왼쪽으로 치우치도록 모델링을 할 수도 있다.
Extraordinary Points
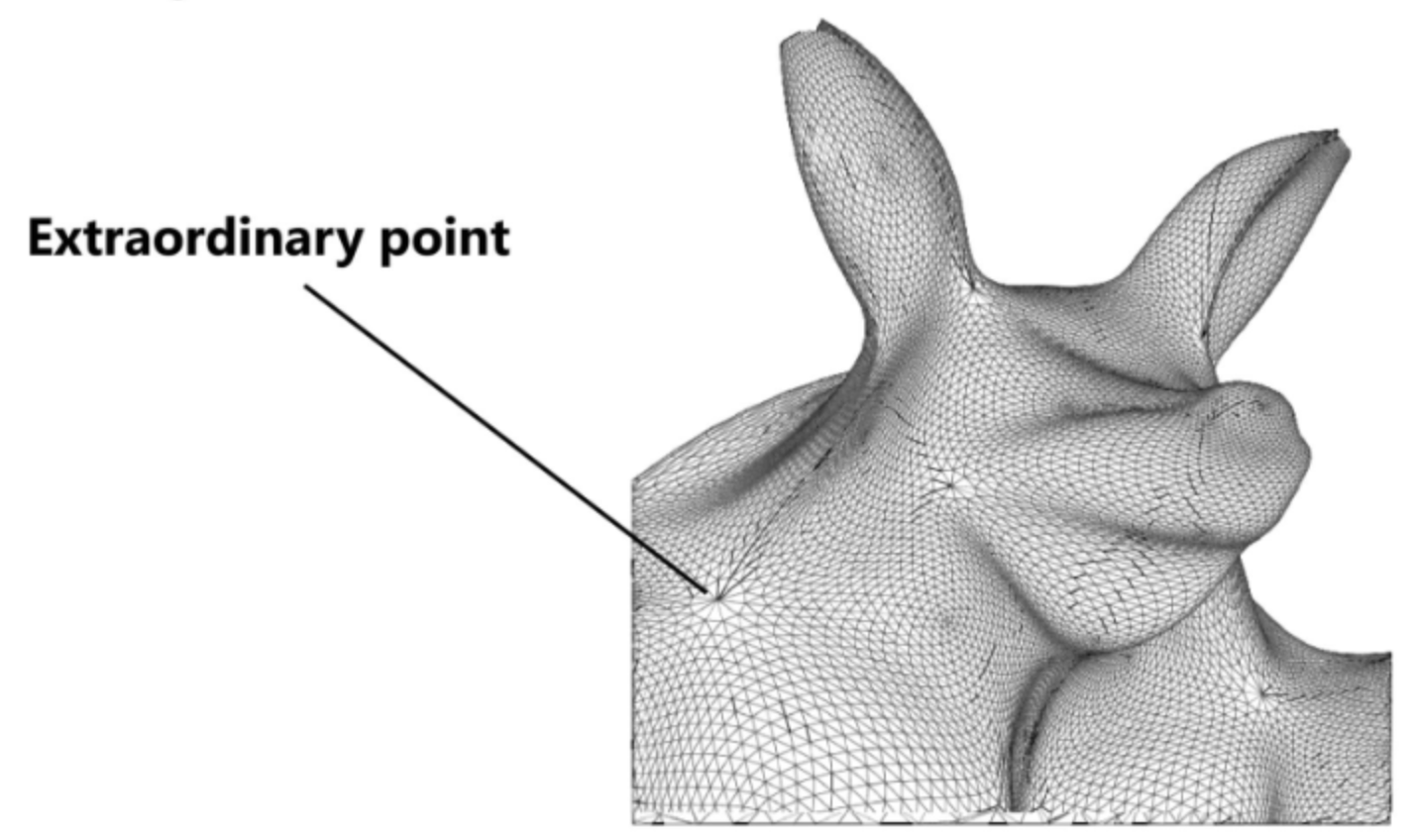
Subdivision을 하다보면, 그물망의 꼭짓점처럼 비정상적인 점이 생길수가 있다.
이 점을 Extraordinary point라고 한다.
Continuity
수학에서 연속성이람은 우극한과 좌극한이 일치하고 함수값도 똑같이 일치했을때를 의미한다.
이러한 연속성은 크게 3단계로 나눈다.
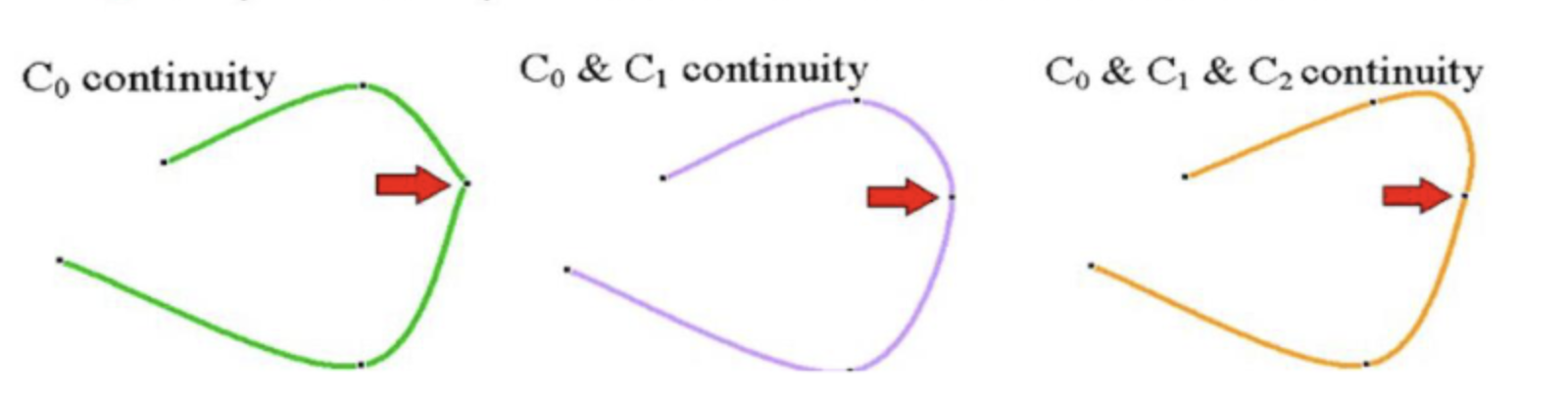
- C0(연속성)
선이 그냥 연결되어 있으면 된다. - C1(미분가능)
뾰족한 곡선이 아닌 기울기값이 연속적인 미분가능하다는 의미이다. - C2(2차미분가능)
이계도함수가 연속적임의 의미하며 좀더 곡선에 근접한 형태이다.
3D 물체 -> 2D 정점으로 변환
Implicit Surface
실제 모델은 각 정점마다의 좌표값이 있고, Topology로 연결되어 있다.
.obj 의 파일인 모델을 가져오면 이런 정보들이 모두 저장되어있다.
물체를 표현할때 충돌이나 물체의 연결을 표현하고 싶으면, 이런 정점과 Topology의 연산을 하나하나 다해야한다.
그러면 컴퓨팅 파워를 너무 많이 사용하게 된다.
그래서 암시적으로 간단히 표현할 수 있는 함수를 만든 것이 Implicit Surface이다.
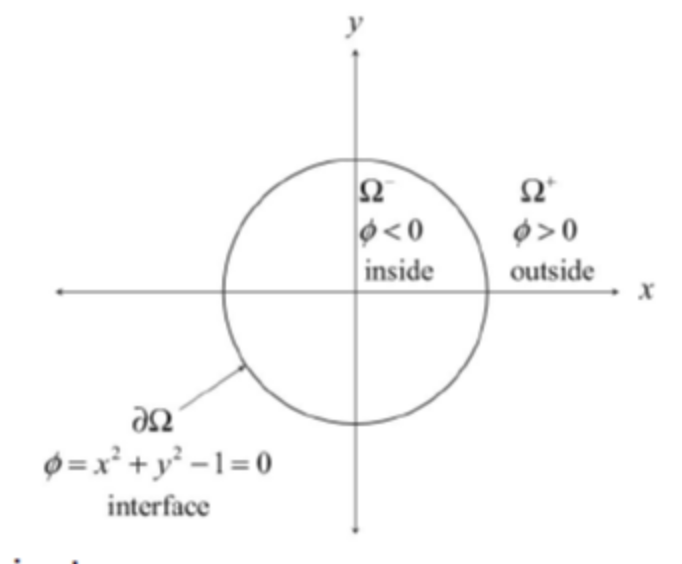
이면 물체의 밖에, 와 동일 이면 물체의 내부에 있는 것이다.
마치 2차방정식의 판별식과 같은 개념이다.
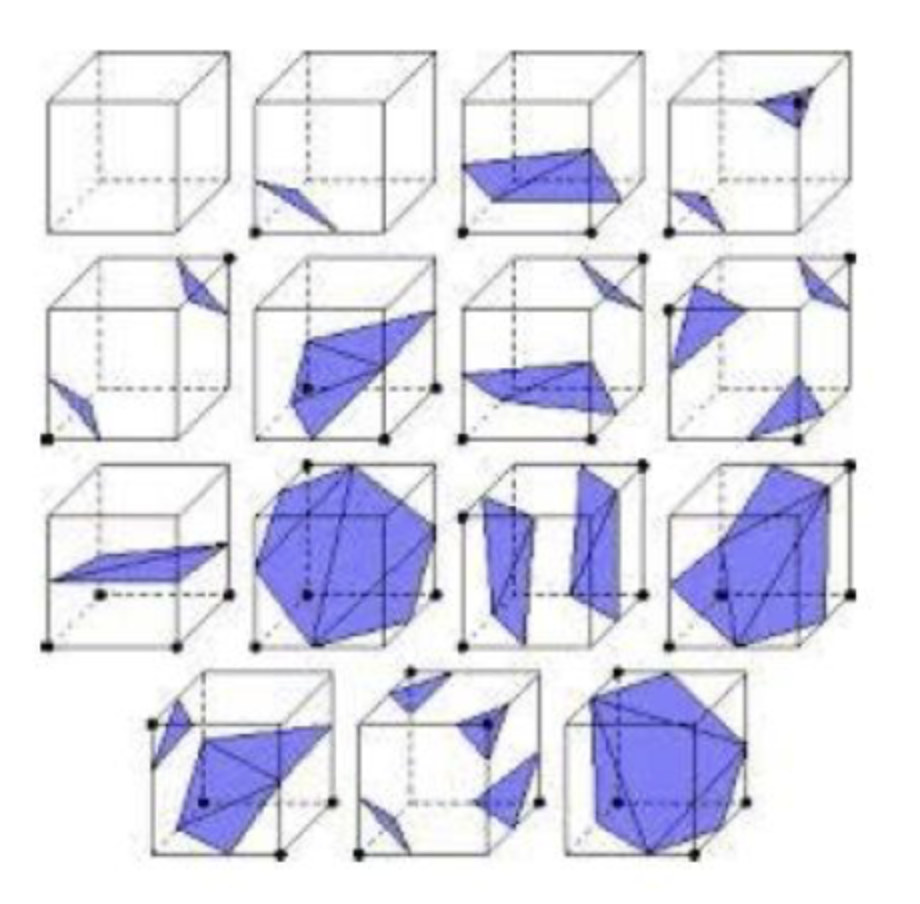
Marching Cubes
Marching Cube를 통해 3차원의 물체를 픽셀들의 그룹으로 나타낼 수 있다.
2D의 과정부터 이해해보면 편하다.
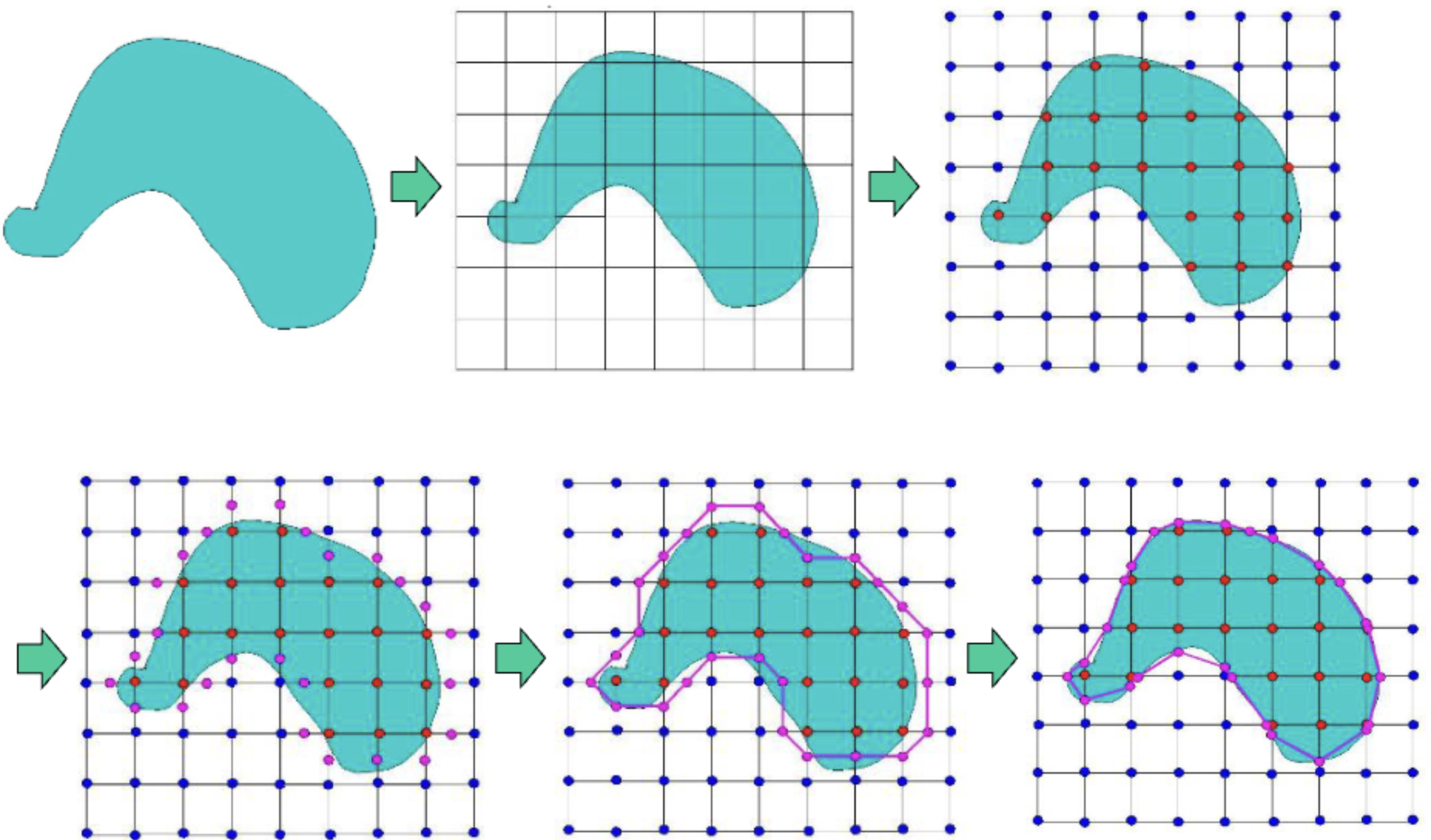
물체가 있는 공간으로 Implicit Surface를 찾아야한다.
Implicit Surface는 정확히 그 물체의 형태를 뜻하는게 아니라 약간의 모양을 따라한 것이다.
위의 사진의 과정은 그림만 봐도 이해가 될것이다.
먼저, 물체를 셀 단위로 나누고, 셀 안에 포함된 점들을 표시한다.
포함된 점에서 한칸 밖에 있는 곳부터 점점 좁혀나가 핑크색 Implicit Surface를 좁혀가며 알맞는 모형을 찾는 것이다.
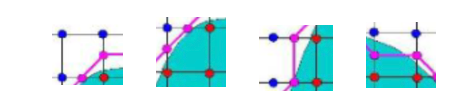
각 셀 내부의 핑크색 선의 형태는 여러가지가 있다.
- 아래에 점, 오른쪽에 점이 연결된 형태
- 왼쪽 점, 윗점이 연결된 형태
- 윗점, 아랫점이 연결된 형태
- 오른쪽점, 왼쪽점이 연결된 형태
이외에도 여러가지의 종류가 있다.
이런 형태를 종류에 맞춰 각 셀마다 종류값을 저장하고 관리하는 것이다.
마치 jpeg의 원리유사하다. 이미지 픽셀마다 종류를 저장하고 거기에 맞추는 형식이니..
그런데 여기서 1,2의 경우는 회전하면 똑같고 3, 4도 회전하면 똑같다.
그래서 사실 2D의 경우 2가지의 종류라고 보면 된다.
3D모델에서는 총 15지가 존재한다.