선형대수 6-5. PCA

• ref 혁펜하임님의 PCA 강의

PCA의 활용 목적

• 데이터의 분포를 가장 잘 설명하는 벡터(aka 주차원 벡터)를 찾고, 이를 활용하여 차원 축소를 하고자 한다
• 가장 잘 설명하는 벡터는 무엇인가?
  1. 분포의 분산이 가장 큰 방향의 벡터
  2. 1.에 수직인 방향의 벡터

PCA 순서

• 표기
  - $\tilde{\boldsymbol{x}} _{i}=\begin{bmatrix} x _{1} \\ x _{2} \\ \cdots \\ x _{n} \end{bmatrix}$ : 평균을 빼지 않은 데이터
  - $\bar{\boldsymbol{x} }=\begin{bmatrix} \overline{x_{1}} \\ \overline{x _{2}} \\ \cdots \\ \overline{x _{n}} \end{bmatrix}$ : 데이터의 평균값
  - $\boldsymbol{x} _{i}=\tilde{\boldsymbol{x}}_{i}-\overline{\boldsymbol{x}_{i}}$ : 평균을 뺀 데이터값
  - $\boldsymbol{u}$ : 어떤 벡터
• 어떤게 가장 잘 설명한다고 할 수 있을 까?
  -
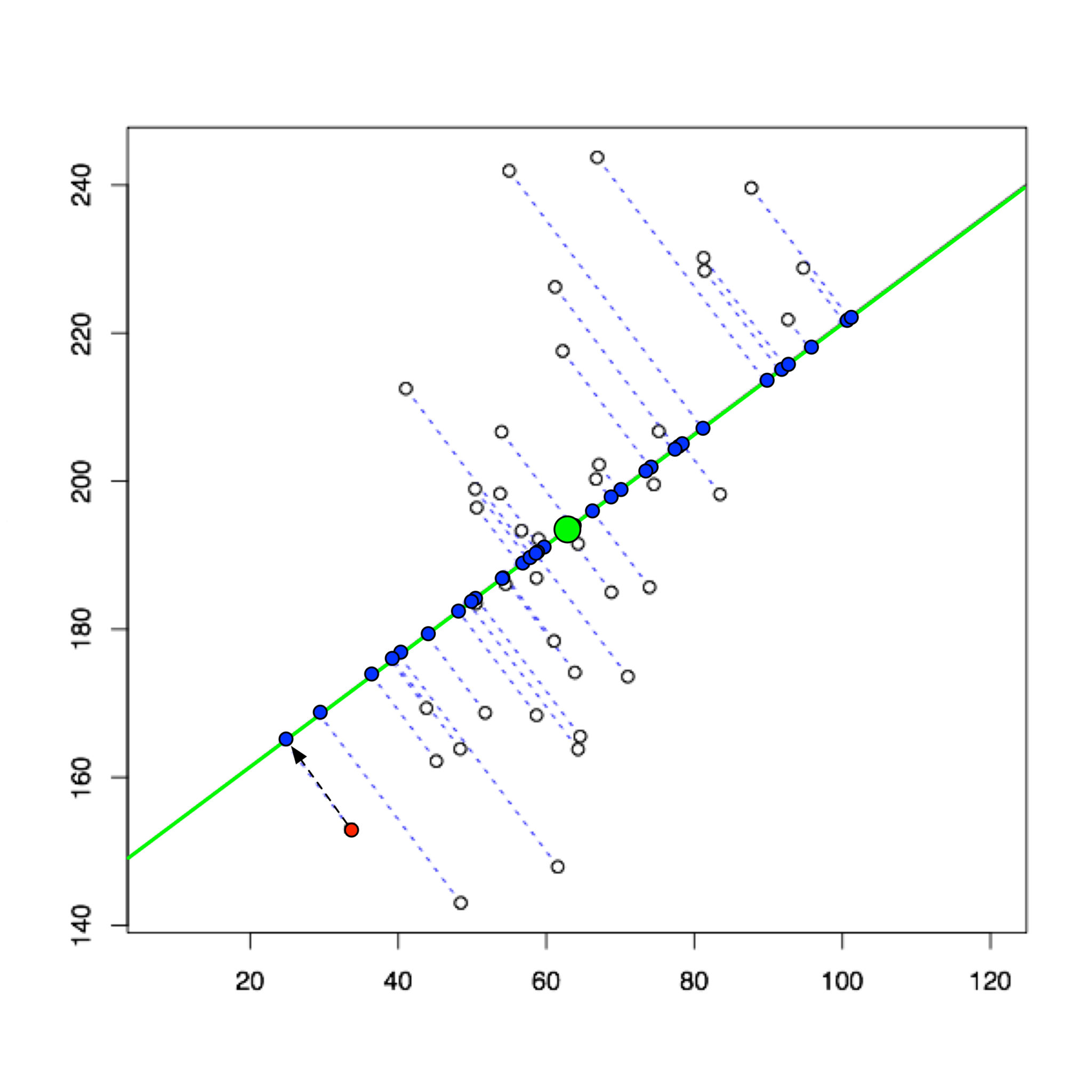
  - 어떤 벡터 $u$ 가 있을 때, $x _{i}$ 와 $u _{i}$ 에 정사영내렸을 때의 가장 짧을경우 가장 잘 설명할 수 있다고 할 수 있을 것이다.
• 수식유도
  - $\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i}^{}{}{(\boldsymbol{x} _{i}-\boldsymbol{x} _{i} ^{T}\boldsymbol{u} \cdot \boldsymbol{u}) ^{T}(\boldsymbol{x} _{i}-\boldsymbol{x} _{i} ^{T}\boldsymbol{u} \cdot \boldsymbol{u})}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i}^{}{(\boldsymbol{x} _{i} ^{T}-(\boldsymbol{x}_{i} ^{T}\boldsymbol{u})\cdot \boldsymbol{u} ^{T})}(\boldsymbol{x}_{i}-\boldsymbol{x}_{i} ^{T}\boldsymbol{u}\cdot \boldsymbol{u})$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i}^{}{\boldsymbol{x}_{i} ^{T}\boldsymbol{x}_{i}-(\boldsymbol{x}_{i} ^{T}\boldsymbol{u}) ^{2}+(\boldsymbol{x}_{i} ^{T}\boldsymbol{u}) ^{2}\boldsymbol{u} ^{T}\boldsymbol{u}}-(\boldsymbol{x}_{i} ^{T}\boldsymbol{u})\boldsymbol{u} ^{T}\boldsymbol{x}_{i}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i}^{}{\boldsymbol{x}_{i} ^{T}\boldsymbol{x}_{i}-\boldsymbol{x}_{i} ^{T}\boldsymbol{u}}\boldsymbol{u} ^{T}\boldsymbol{x}_{i}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{-1}{N}\displaystyle\sum\limits_{i}^{}{\boldsymbol{x}_{i} ^{T}\boldsymbol{u}}\boldsymbol{u} ^{T}\boldsymbol{x}_{i}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{-1}{N}\displaystyle\sum\limits_{i}^{}{\boldsymbol{u} ^{T}\boldsymbol{x}_{i}\boldsymbol{x}_{i} ^{T}\boldsymbol{u}}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{-1}{N}\boldsymbol{u} ^{T}\displaystyle\sum\limits_{i}^{}{\boldsymbol{x}_{i}\boldsymbol{x}_{i} ^{T}}\boldsymbol{u}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\displaystyle\frac{-1}{N}\boldsymbol{u} ^{T}\displaystyle\sum\limits_{i}^{}{(\tilde{\boldsymbol{x}_{i}}-\overline{\boldsymbol{x}})(\tilde{\boldsymbol{x}_{i}}-\overline{\boldsymbol{x}}) ^{T}}\boldsymbol{u}$
  - $=\min\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}-\boldsymbol{u} ^{T}\boldsymbol{R} _{d}\boldsymbol{u}$ ( $\boldsymbol{R} _{d}$ 는 N-1로 나눠주는 것으므로 정확한 정의는 아니지만 N이 충분히 크면 $N \sim N-1$ 이므로 표본공분산이라 칭함)
  - $=\max\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\boldsymbol{u} ^{T}\boldsymbol{R} _{d}\boldsymbol{u}$
  - $L= \boldsymbol{u} ^{T}\boldsymbol{R} _{d}\boldsymbol{u}+\lambda(1-\boldsymbol{u} ^{T}\boldsymbol{u})$
  - $\cfrac{\partial {L}}{\partial {\boldsymbol{u}}}=2\boldsymbol{R} _{d}\boldsymbol{u}-2\lambda \boldsymbol{u}$
  - $(\boldsymbol{R}_{d}-\lambda)\boldsymbol{u}=0$
  - ($\displaystyle\frac{\partial {\boldsymbol{x}\boldsymbol{A}\boldsymbol{x}}}{\partial {\boldsymbol{x}}}=2\boldsymbol{A}\boldsymbol{x}$ )
  - 즉 $\boldsymbol{u}$ 는 $\boldsymbol{R}_{d}$ 의 고유벡터이다
  - $Cov(\boldsymbol{x},\boldsymbol{x})$ 는 대각화가능하므로
  - $\max\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\boldsymbol{u} ^{T}\boldsymbol{R} _{d}\boldsymbol{u}$
  - $=\max\limits_{{u\text{ .s.t.}\| u \| ^{2}=1}}\boldsymbol{u} ^{T}(\displaystyle\sum\limits_{i=1}^{n}{\lambda _{i}}\boldsymbol{q} _{i})\boldsymbol{u}$ ($\lambda _{i},\boldsymbol{q} _{i}$는 $Cov(\boldsymbol{x},\boldsymbol{x})$의 고유값,그에 대응되는 정규직교벡터. $\lambda _{1}<\lambda _{2}< \cdots$ 라고 하자)
  - $\boldsymbol{u}$ 는 가장 큰 고유값에 대응되는 정규직교벡터 $\boldsymbol{q}_{1}$ ($\| \boldsymbol{q}_{1} \|=1$)일때 가장 큰 값을 갖는다
• 차원축소
  - $\hat{\boldsymbol{x}}_{i}=\boldsymbol{x} ^{T}\boldsymbol{q}_{1}\cdot \boldsymbol{q} _{1}+\boldsymbol{x} ^{T}\boldsymbol{q}_{2}\cdot \boldsymbol{q} _{2}+\cdots$
• SVD와 PCA의 차이
  - SVD는 하나의 데이터에 대한 개별적 압축
  - PCA는 전체 데이터에 대한 집단적 압축
• 예) 100X100 얼굴 인식
  - 이미지 데이터 차원은 10000
  - 10차원으로 줄인다고 하면
  - $\displaystyle\sum\limits_{i=1}^{10}{\boldsymbol{x}_{i} ^{T}\boldsymbol{q}_{i}\cdot \boldsymbol{q }_{i}} \sim \boldsymbol{x}_{i}$
  - $=\boldsymbol{x}_{i} ^{T}[\boldsymbol{q}_{1},\boldsymbol{q}_{2},\cdots,\boldsymbol{q}_{10}]\begin{bmatrix} \boldsymbol{q}_{1} ^{T} \\ \boldsymbol{q}_{2} ^{T} \\ \cdots \\ \boldsymbol{q}_{10} ^{T}\end{bmatrix}$
  - encoder-decoder로 해석할 수 있다
• manifold learning은?
  - 기존 PCA는 데이터의 정보를 가장 잘 보존할 수 있는 hyperplane을 찾는($\displaystyle\sum\limits_{i}^{}{a _{i}x _{i}}=0$ 꼴) 반면에 manifold learning은 다차원의 곡면, manifold를 찾는 것이다