124나라의 숫자

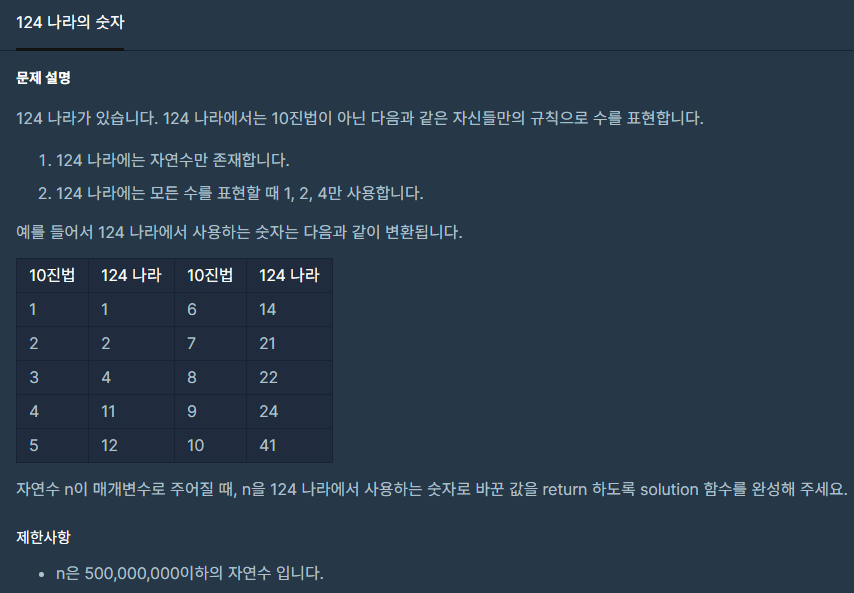
🔒 문제

💡 생각의 흐름

먼저, 10진수 -> 124나라의 숫자가 바로 생각나지 않으니
124나라의 숫자 -> 10진수변환을 곱씹어 보았다.
예를들면 10진수 '241'
3^2 x 2 + 3^1 x 4 + 3^0 x 1

[0단계]
3마다 단위가 바뀌는 걸로 봐서 3진법!!!!!?!?!?! 근데 숫자 0과 4를 따로 처리해야겠네?
[1단계]
124나라의 숫자의 길이 == 3^1 + 3^2 + 3^3 + .... 3의 제곱수의 누적합이 더 커지는 단계이다.
예를 들면 '20'이라는 10진수는 3 + 9 + (27) 에서 3+9 까지의 합보다 크고 27보다 작으므로 3자리.
[2단계]
1단계에서 구한 길이를 length 라고 하면 3^length-1 N + 3^length-2 M + ... 3^0 * K
뒤에 곱해진 수 NM...K 가 곧 124나라의 숫자이다.

😅 실수

0과 4처리에서 실수가 있었다.
모든 자리수에 0이 올 수 없으므로 큰 자리수부터 더하는 '2단계' 방식을 따를경우 나머지 자리수에 1이 올 수 있도록 나머지를 남겨야한다.
EX) 10진수 30=> 3^2 3 + 3^1 1 + 3^0 * 0
⚠️ 0은 구조적으로 올 수 가 없다!!!

🔑풀이 (Java)

import java.util.ArrayList;
import java.util.Arrays;

class Solution {
    static int totalSum = 0, length = 0;

    // 3진법과 유사하나 0이란 숫자가 존재하지 않으므로 모든 자리수마다 1 이상의 숫자를 남김
    // -> 결국 totalSum + 1 의 자리를 MSB부터 내려가면서 매번 남겨야함 (ex 1, 4, 12, 39...)
    static ArrayList<Integer> positionTotalSum = new ArrayList<Integer>(Arrays.asList(0, 1));

    // 1단계 124나라 숫자 길이 구하기, length 에 124나라 숫자 길이가 초기화됨.
    static void getNumberOfDigit(int number) {
        do {
            totalSum += Math.pow(3, ++length);
            positionTotalSum.add(totalSum + 1);
        } while (number > totalSum);
    }

    public String solution(int n) {
        //        자릿수 결정 -> length 구해짐
        getNumberOfDigit(n);

        var stringBuilder = new StringBuilder();

        // 2단계 MSB 부터 구하기
        for (int m = length - 1; m >= 0 ; m--) {
            var powerOfThree = (int) Math.pow(3, m);
            int quotient = (int) (n / powerOfThree);
            int remainder = (int) (n % powerOfThree);
            // 남은 자리수에 1이 올 수 있는지 검사
            if (remainder >= positionTotalSum.get(m)) {
                n = remainder;
            } else {
                quotient--;
                n = remainder + powerOfThree;
            }
            if ((quotient == 3)) stringBuilder.append(4);
            else stringBuilder.append(quotient);
        }
        return stringBuilder.toString();
    }
}