
정렬은 우리가 평상시 꾸준히 해왔던 일상과 관련되어 있다.
- 옷장 의류 무지개 색상에 따른 정리
- 냉장고 음식 유통기한에 따른 최신 정리
- 도서관 책 장르에 따른 정리 및 가나다, ABC, 123 문자 순서에 따른 정리
쉽게 정리하자면 한 요소에 순서에 따른 정리이다.
컴퓨터 알고리즘 세계에서도 데이터를 순서에 따른 분류별 정리가 필요한데
그때 쓰이는 알고리즘이 바로 정렬(sorting)이다.
정렬 알고리즘의 여러 방법에 대해 알아보자
Bubble Sort
function bubbleSort (arr) {
for(let i = 0; i < arr.length; i++) {
for(let j = 0; j < arr.length -1 - i; j++) {
if(arr[j] > arr[j + 1]) {
let swap = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = swap
}
}
}
return arr
}
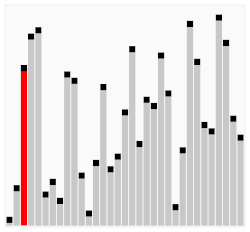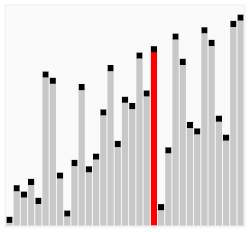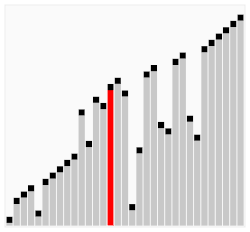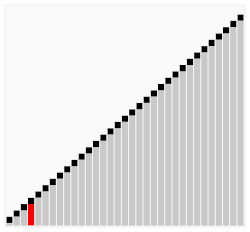
해당 요소가 연쇄적으로 오른쪽 요소와 비교하여 크면 이동 작으면 비교 대상 요소가 바뀌는 특징을 갖고 있다.
bubble shot 메커니즘을 상세하게 그림 예시로 설명하겠다.
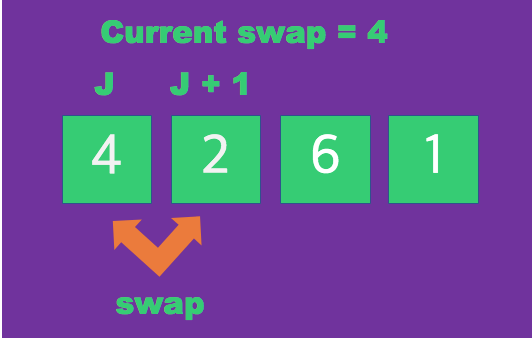
첫 요소 J는 현재 swap 변수에 할당되어 있으며 크기가 더 크므로 J + 1와 순서 교체를 한다.

J + 1이 더 크므로 swap이 6이라는 값을 할당하며 다음 인덱스로 넘어간다.
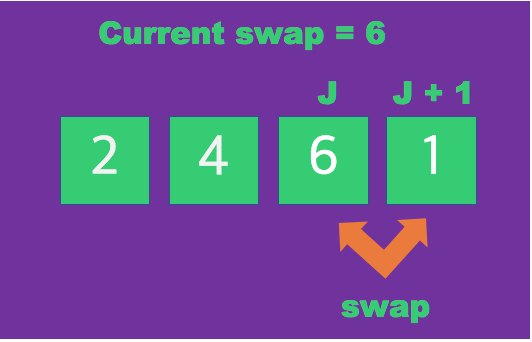
J가 큰 관계로 최종 마지막 인덱스 순서에 이동되어 반복문이 마치게 된다.

Big O
Best case: O(n)
배열의 정렬이 순서에 맞게 이루어질 경우
Worst Case: O(n^2)
배열의 정렬이 순서에 안맞게 이루어질 경우
배열의 요소가 많을수록 시간복잡도에 따라 성능이 매우 안좋으며, 별도의 배열을 직접 생성하여
정렬을 맞출 필요가 없어 해당 코드의 메모리가 절약된다.
Select Sort
function selectSort (arr) {
for(let i = 0; i < arr.length; i++) {
let min = i
for(let j = i + 1; j < arr.length; j++) {
if(arr[min] > arr[j]) {
min = j
}
}
if(min !== i) {
let swap = arr[min]
arr[min] = arr[i]
arr[i] = swap
}
}
return arr
}
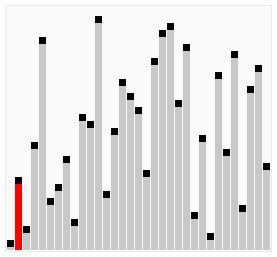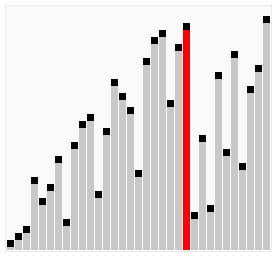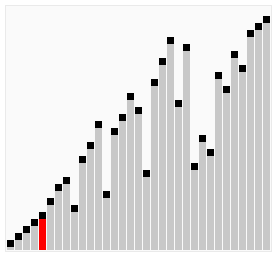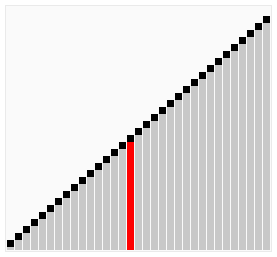
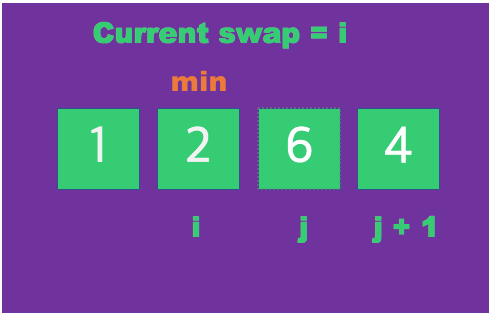
해당 요소 중 최소값을 찾아 첫번째 인덱스 요소에 할당하며 순차적으로 계속 정렬한다.
즉 첫번째 요소가 가장 작은 숫자에 해당된다.

i의 첫번째 요소 가장 작은 숫자는 1이 되어 j+2와 자리가 교체 된다.
i 의 두번째 요소는 이미 두번째로 가장 작은 숫자이므로 배열 요소가 교체될 필요가 없다.

i 의 세번째 요소는 마지막 요소 4보다 더 크므로 마지막 인덱스에 해당되는 요소가 된다.

Big O
Best case: O(n^2)
배열의 정렬이 순서에 맞게 이루어질 경우
Worst Case: O(n^2)
배열의 정렬이 순서에 안맞게 이루어질 경우
위 2번째 그림의 경우 이미 2번째 요소가 작은 요소값이 맞지만 순차적으로 의미없이 진행되므로 비효율적이다.
insertion Sort
function insertionSort(arr) {
for(let i = 1; i < arr.length; i ++) {
let cur = arr[i]
let left = i - 1
while(left >= 0) {
if(arr[left] > arr[left + 1]) {
arr[left + 1] = arr[left]
arr[left] = cur
}
left--
}
}
return arr
}
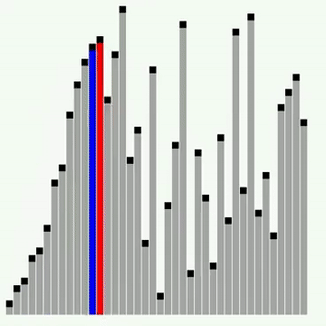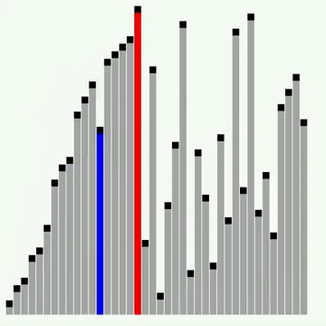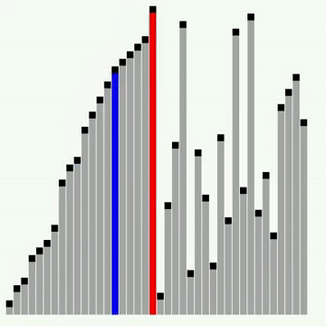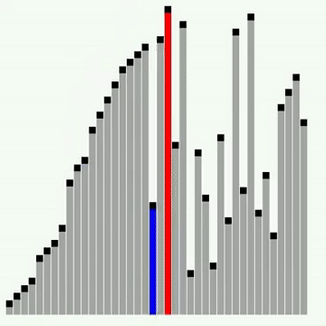
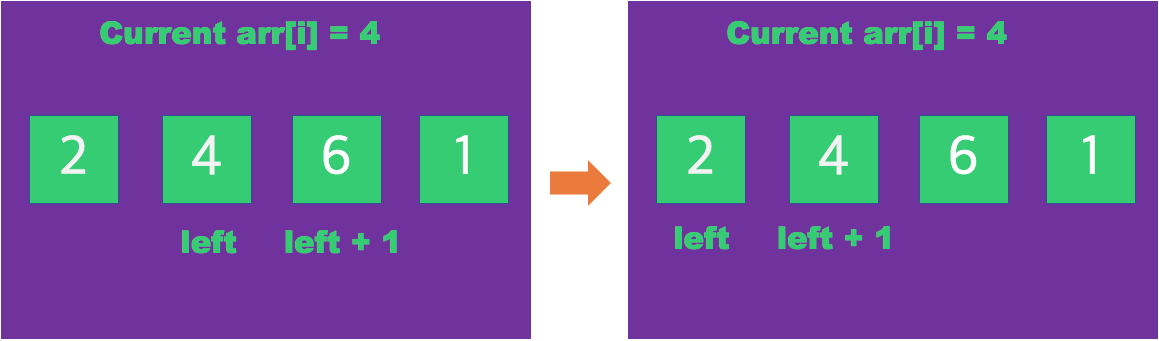
cur 변수는 현재 해당 요소 값을 반복 할당하여 앞의 요소가 크면 새로 삽입하여 자리가 최신화 된다.

left 보다 left + 1이 작으므로 각자 자리가 교체되어 삽입된다.
4의 요소값이 같으므로 cur arr[i] 변수가 전의 값과 똑같으며 변화가 없다.

cur arr[i] 변수의 값은 새로 바뀌게 되고 left + 1이 left 보다 작으므로 각자 자리가 새로 삽입된다.
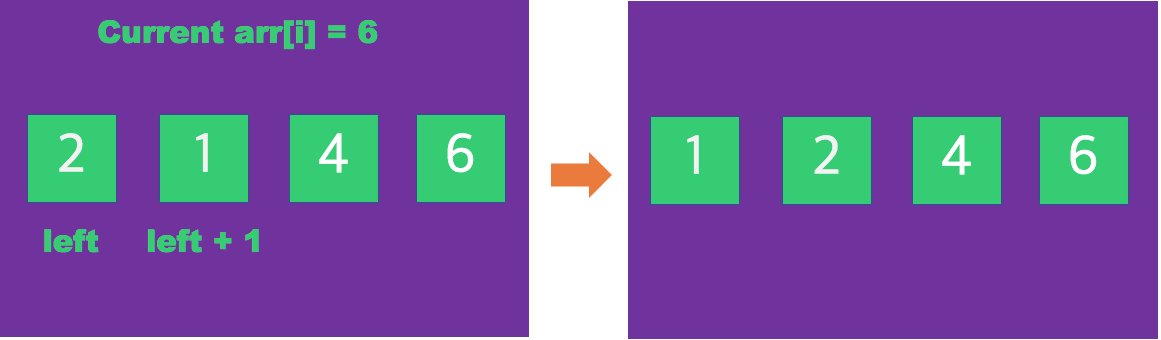
left-- 후위감소 효과로 인해 전의 요소로 서로 비교하며 1의 요소는 순차적으로 비교 메커니즘을 통해 최종적으로
첫번째 요소 자리에 삽입되게 되며, 정렬이 끝 마친다.
Big O
Best case: O(n)
배열의 정렬이 순서에 맞게 이루어질 경우
Worst Case: O(n^2)
배열의 정렬이 순서에 안맞게 이루어질 경우
bubble sort와 같이 배열의 요소가 많을수록 시간복잡도 효율이 떨어진다.
quick sort
function quickSort(arr) {
if(arr.length <= 1) {
return arr
}
let cur = arr[0]
let left = []
let right = []
for(let i = 1; i < arr.length; i++) {
if(cur > arr[i]) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
let leftArr = quickSort(left)
let rightArr = quickSort(right)
return [...leftArr, cur, ...rightArr]
}
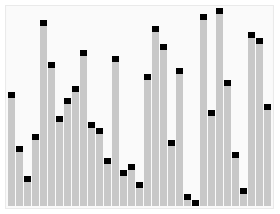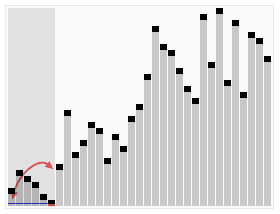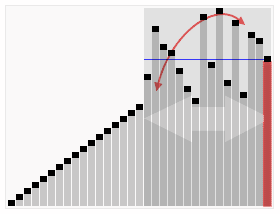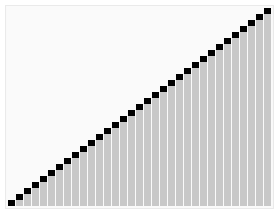
in place 메모리 사용법에 의존하여 좌측 배열, 우측 배열로 나눠져 있다.
원본 배열에서 값이 작을수록 좌측, 반대로 클수록 우측에 저장되는 개념이며, 기준이 되는 원소를 하나 지정하여
재귀함수를 통해 좌측, 우측이 연쇄적으로 비교하여 재귀 베이스를 만나는 순간 그동안 모은 배열을 각 변수에 저장한다.

먼저 주어진 배열에서 cur 기준이 될 요소를 지정한다.
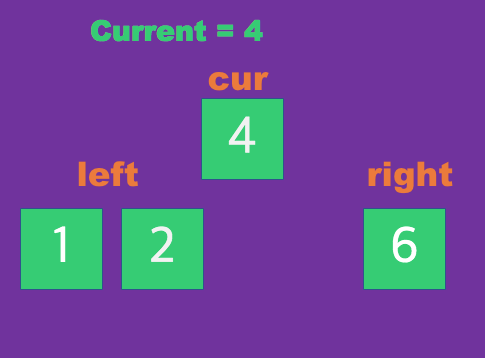
cur의 기준으로 작으면 left배열, 크면 right 배열에 각각 저장한다.

재귀함수를 통해 left, right 배열 각각 기준이 될 요소를 지정 후 똑같이 각 배열에 저장한다.
right의 경우 이미 하나 밖에 없는 요소이므로 재귀 베이스를 통해 [2]라는 결과가 나온 상태이다.

left의 우측 배열이 드디어 최종적으로 순회하였으므로 결국 [1, 2] 결과가 도출되었다.

return [...leftArr, cur, ...rightArr] 왼쪽의 비교 배열, 기준 요소, 오른쪽의 비교 배열을
각 나란히 입력하면 정렬화된 코드가 출력된다.
Big O
Best case: O(nlog₂n)
배열의 left, rigth 비교가 공평히 이루어질 경우
Worst Case: O(n^2)
배열의 기존 정렬 상태가 오름차순 정렬 or 내림차순 정렬로 이루어질 경우
