소수 (prime number)
1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수

소수를 구하기 위해선 간단히 해당 숫자에 관해 나머지가 0이 나오나 안나오냐에 따라

판별하면 쉽게 해결 할수 있는 문제이다.

해당 방식을 코드로 구현해보자

function isPrime(n) {
   let result = 1
   
   for(let i = 3; i <= n; i++) {
       let check = 0
       for(let j = 2; j <= i; j++) {
           if(i % j === 0 && i !== j) {
               check = 0
               break;
           } else if(i % j !== 0) {
               check = j
           }
       }
           if(check) {
               result++
           }
   }
   return result;   
}

0, 1를 제외하고 2까지 소수를 판별해놓은 상태에서 코드를 구현 해보았다.

그러나 n 인자가 100000으로 선언할 경우 결과가 출력되는데 5~6초가 소요된다.

이는 결국 시간 복잡도에 따라 효율성이 매우 떨어지는 코드이므로 리펙토링을 하여야 한다.

에라토스테네스의 체

고대 그리스 학자 에라토스테네스가 발견한 에라토스테네스의 체의 패턴은 다음과 같다.

1을 제외한 2부터 배수를 진행하여 원하는 n의 숫자가 초과될 경우

3의 배수를 다시 순차적으로 진행하다 보면 결국 각각 배수는

이미 한번씩 순회를 하였으므로 2번 맞닥뜨릴 일이 없어진다.

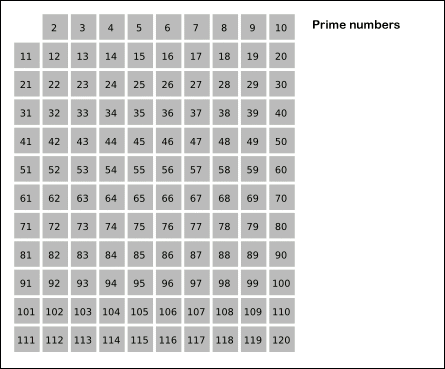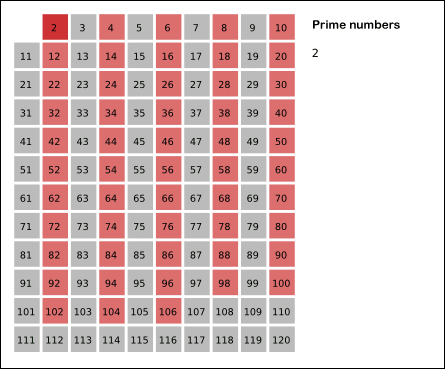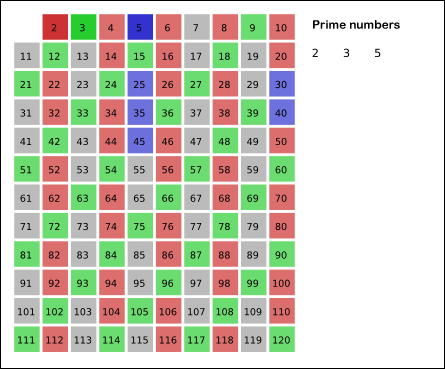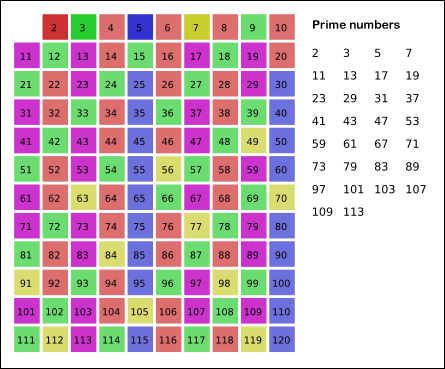
쉽게 생각하자면 그냥 단순히 빈 공간을 점차 채운다고 보면 좋다.

코드 구현

function isPrime(n) {
    let arr = Array(n+1).fill(true)
    arr.splice(0, 2, false, false)
    
    for(let i = 2; i <= n; i++) {
    
        if(arr[i]) {
            for(let j = i * i; j <= n; j = j + i) {
                arr[j] = false
            }
        }
    }
    
    return arr.filter(el => el === true).length
}

우선 해당 코드를 배열에 묶여 소수일 경우 true, 소수가 아닐 경우 false로 판별한다.

0과 1은 소수 판별 제외 대상이므로 splice() 문법을 통해 false로 변경한다.

(n이 10일 경우 [false, false, true, true, true, true, true, true, true, true, true])

반복문 i가 2부터 순회 (n = 10)
i x i = 4 => i x i = 36 (이미 n의 값을 넘어버린 관계로 종결)
i x i = 9 => i x i = 144 (이미 n의 값을 넘어버린 관계로 종결)

2부터 시작하여 앞서 에라토스테네스의 체 공식에 따른 제곱으로 연쇄 증가를 한다.

어차피 2의 제곱 4로 시작을 하는 이유는 첫번째 배수인 2나 3, 5는 첫 시작점이므로 소수이기에 판별할
이유가 없다.

j의 증가 또한 ++을 후위 혹은 전위 증가로 할 경우 결국 1씩 증가되므로 멀쩡한 소수값에도 false로 할당하기에

배수의 i를 연속적으로 더해주면 된다.

해당 코드는 결국 소수가 아닌 숫자만 false에 할당되는 셈이다.

결론

에라토스테네스의 체를 구현한 코드로 다시 n이 100000 높은 숫자로 입력하면

출력 로딩 없이 바로 결과가 출력된다.

만일 소수 찾기 알고리즘을 구현할 경우 단순 코드로 구현하는 것에는 한계가 있으므로

에라토스테네스의 체를 응용하여 도출하는 방법이 훨씬 최적화된 코드가 될 것이다.