Tree 구조의 개념

자료구조에서 트리는 이름처럼 나무가 가지를 이루듯 정점(Node)과 간선(Edge)으로 구성된 특수 형태이다.

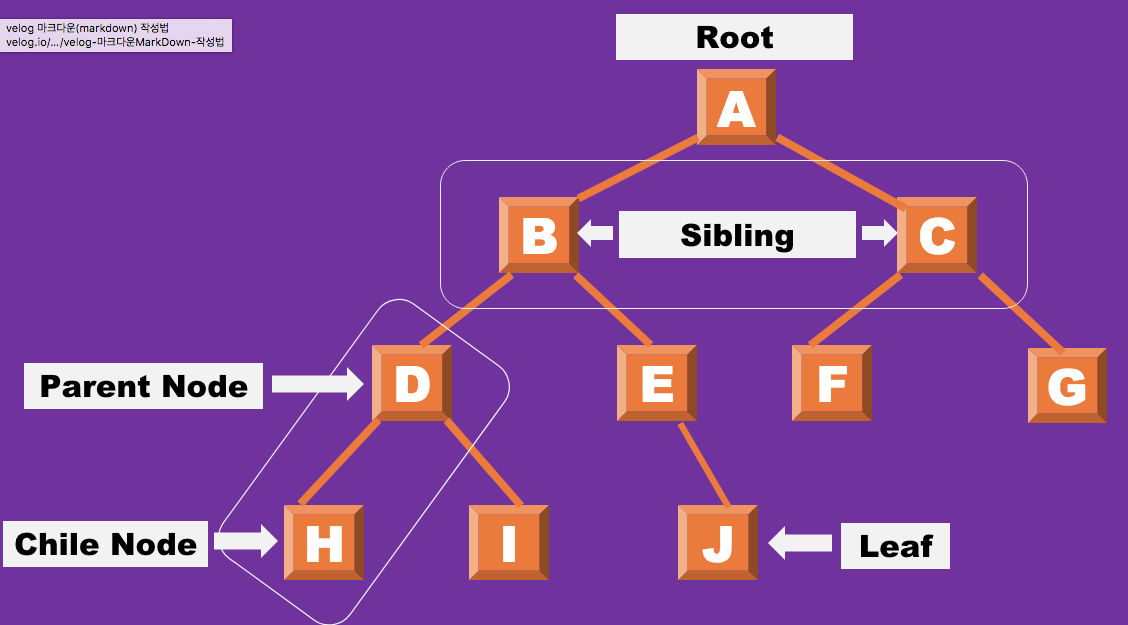
• 노드(Node): 트리의 기본 정점이며 자료 항목 요소
• 루트(Root): 트리 구조의 최상단에 있는 노드
• 가지(Edge): 노드와 노드 간의 연결 간선
• 부모 노드(Parent node): 두 노드 간의 상하관계가 이루어지며 상단에 있는 노드
• 자식 노드(Child node): 두 노드 간의 상하관계가 이루어지며 하단에 있는 노드
• 리프(Leaf): 트리 구조의 종착점이므로 더이상 자식 노드가 없는 노드

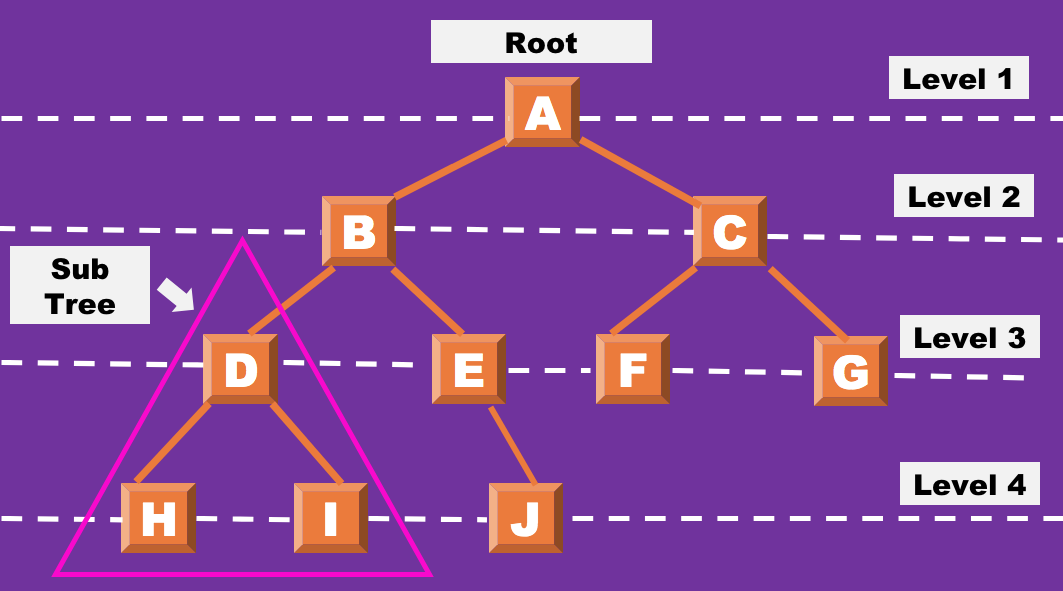
• 레벨(Level): 트리의 같은 깊이끼리 묶은 라인
• 서브 트리(Sub tree): root의 하단에 있는 노드들이 구성된 별도의 트리

트리는 사이클이 없으며 루트에 원하는 노드를 갈 경우 경로는 무조건 하나 밖에 존재하지 않는다.

오직 한개의 루트 노드만이 있으며, 자식 노드 또한 한개의 부모 노드를 가지고 있다.

Tree의 종류

이진 트리

• 전위 순회

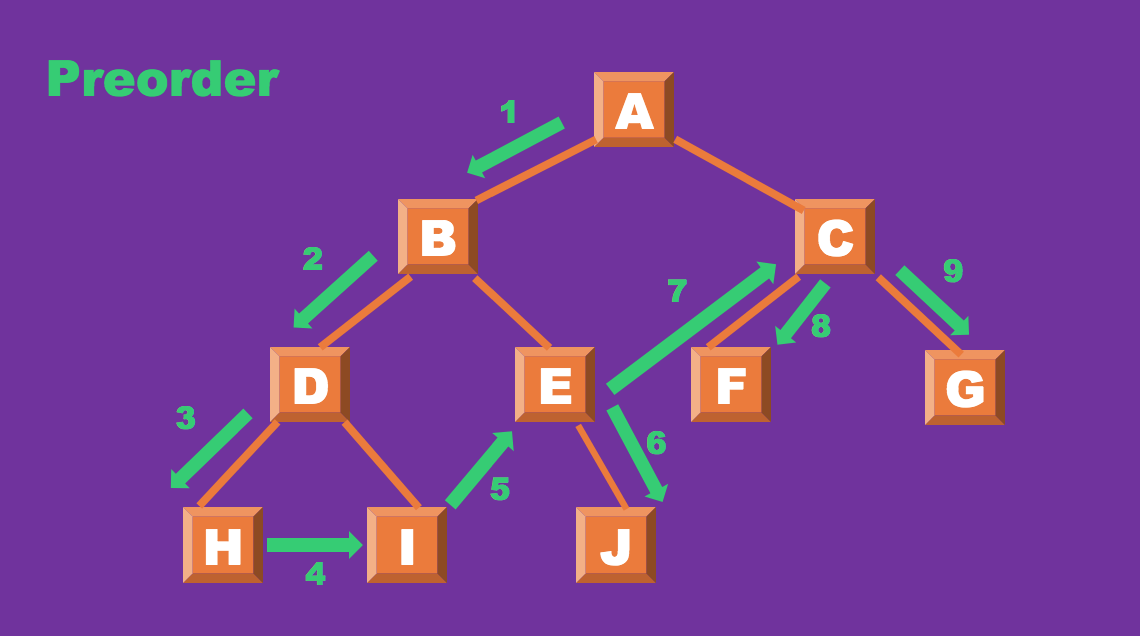
가장 왼쪽 노드의 리프를 기준으로 순차적 순회한 다음 오른쪽 노드로 이동하여 똑같은 패턴에 탐색 한다.

• 중위 순회

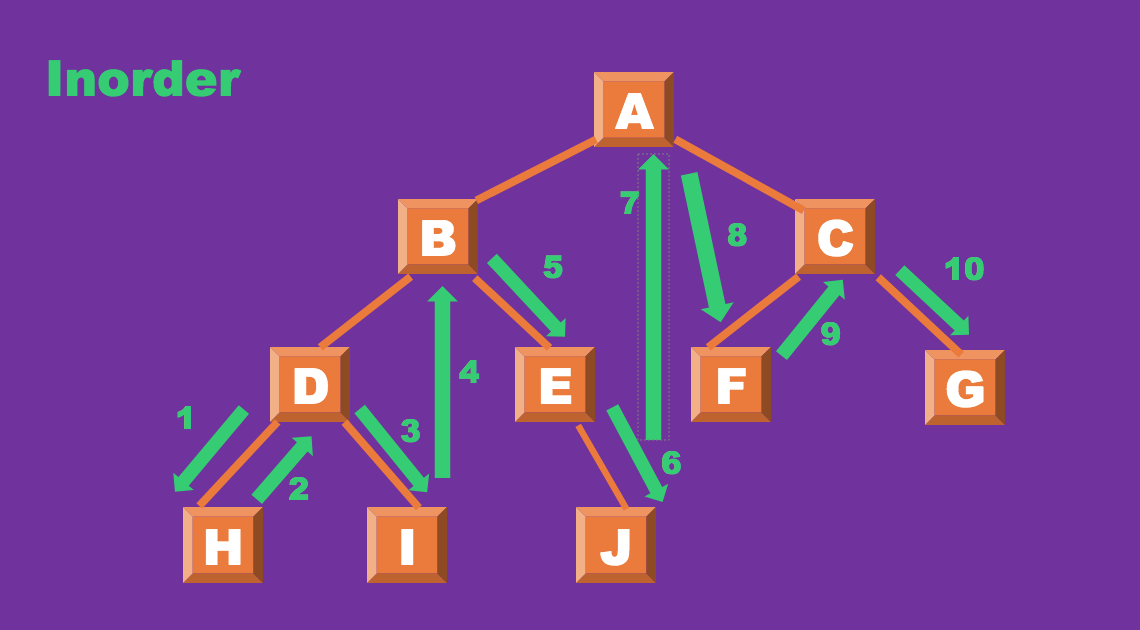
가장 왼쪽 노드의 서브 트리에 있는 리프를 기준으로 순회한 다음 최상단 루트를 탐색후

똑같은 패턴으로 오른쪽 노드도 이동하여 탐색한다.

• 후위 순회

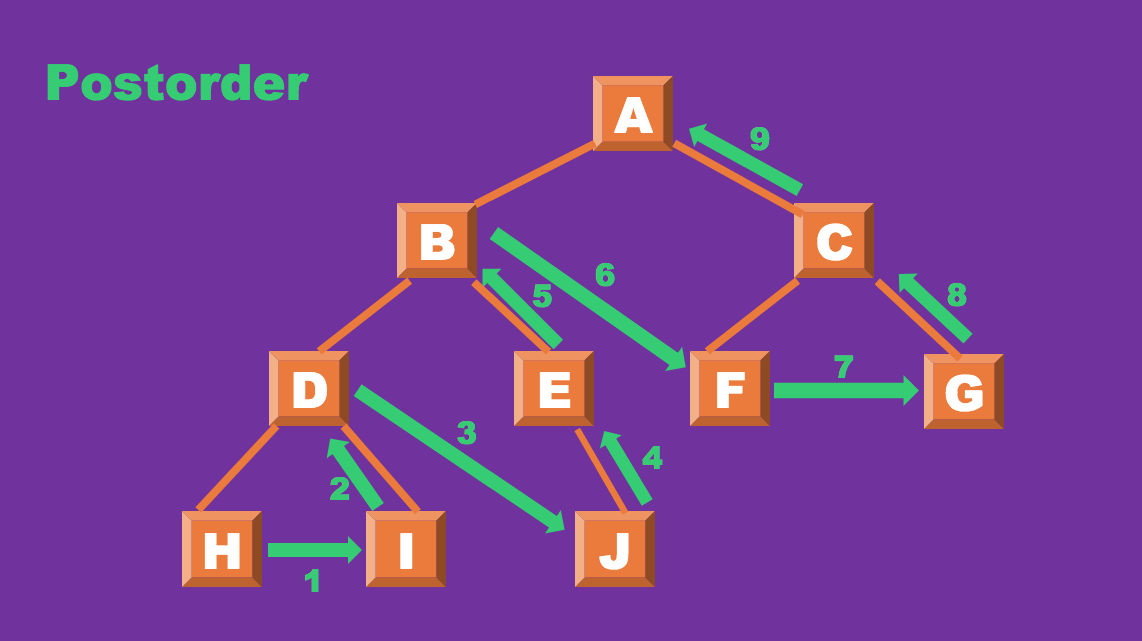
가장 왼쪽 노드의 리프부터 순회하여 오른쪽 노드로 이동하여 순차적으로 순회를 돌고 난 후

최종적으로 루트를 탐색한다.

Binary Search Tree

이진 탐색 트리(Binary Search Tree)는 찾고자 하는 노드가 있을 경우 모든 왼쪽 노드 혹은

모든 오른쪽 노드를 탐색하는 알고리즘이다.

let nums = [2, 7, 8, 9, 10, 13, 17, 19, 21];

function binarySeach(array, target) {
    let left = 0
    let right = nums.length - 1

    while(left < right) {
        let mid = parseInt((left + right) / 2)
        
        if(target === nums[mid]) {
            return mid
        }

        if(target < nums[mid]) {
            right = mid - 1
        } else {
            left = mid + 1
        }
    }

    return false
}

console.log(binarySeach(nums, 7) // 1

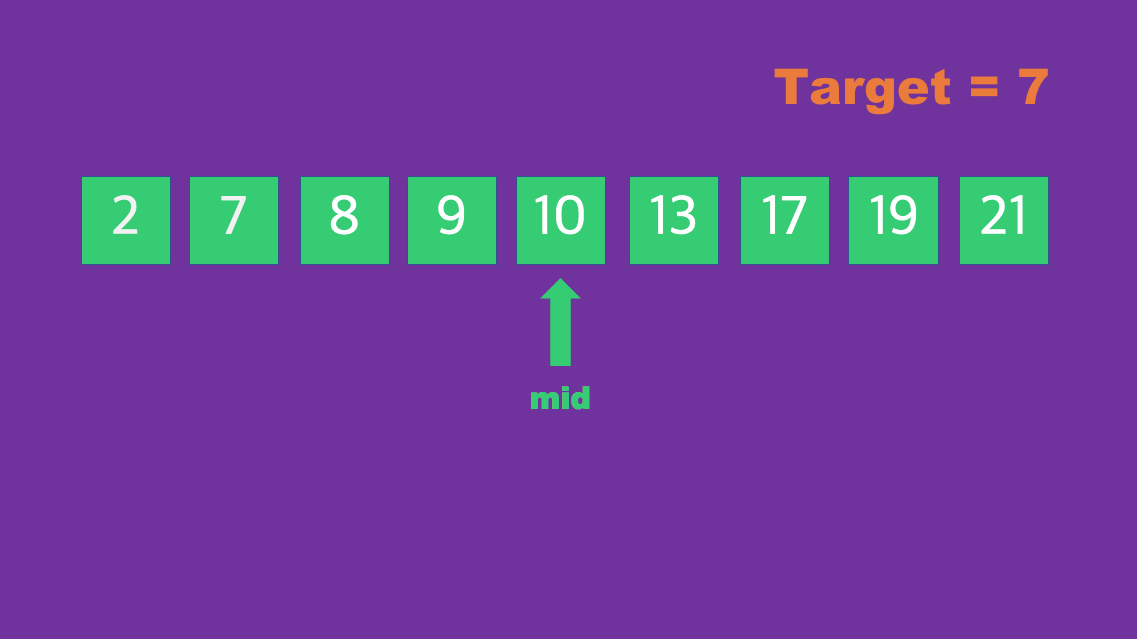
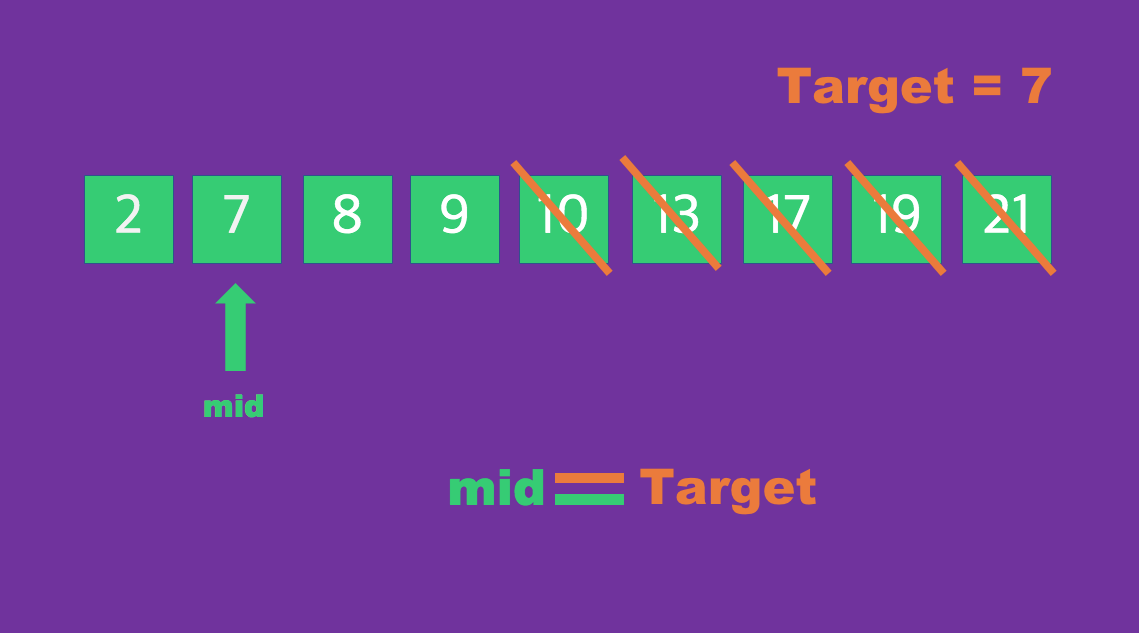
해당 코드를 해석하자면 target 변수가 7이며 9개의 배열 인덱스를 탐색하여 찾아내야 한다.

먼저 해당 인덱스의 중앙값 mid를 정하여 2가지 상황에 따라 배열 인덱스를 제거 한다.

1. mid 인덱스보다 target이 작을 경우 right는 mid - 1로 내린다.
2. mid 인덱스보다 target이 클 경우 left는 mid + 1로 올린다.

만일 최종적으로 하나씩 순회하여 target을 만족하는 배열의 요소가 없다면 false로 종결된다.

재귀함수를 응용한 binary search

let nums = [2, 7, 8, 9, 10, 13, 17, 19, 21];

function binarySeach(array, target) {
	return binarySeachAdd(array, target, 0, array.length - 1)
}

function binarySeachAdd(array, target, left, right) {

  	if(left > right) {
		return false
	}
  
        let mid = parseInt((left + right) / 2)
        
        if(target === array[mid]) {
            return mid
        }
        else if(target < array[mid]) {
          return binarySeachAdd(array, target, left, mid - 1)
        } else {
           return binarySeachAdd(array, target, mid + 1, right)
        }

}

console.log(binarySeach(nums, 25)) // false