function solution(d, budget) {
    
    d.sort((x, y) => x - y)
    
    let total = 0
    let count = 0
    
    for(let i = 0; i < d.length; i++) {
        total = total + d[i]
        if(total > budget) {
            break
        }
        count++
    }
    return count
}

이번 문제는 sort() 메서드로 정렬만 해주면 출력 예시에 절반은 도달했다고 보면 되는 문제였다.

막상 별 어려운 문제도 아닌데 나는 각각 인덱스를 다 더할려면 bubbleshot 알고리즘처럼 각각 더해줘야

하는지 쓸때 없는 고민을 너무 하였다.

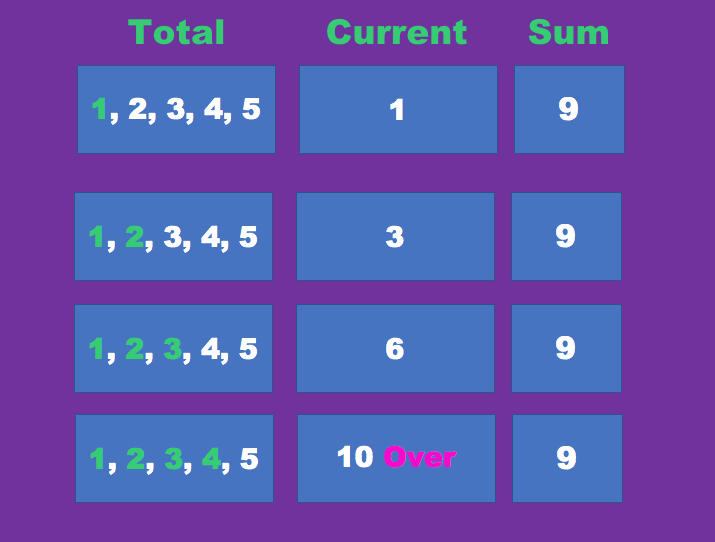
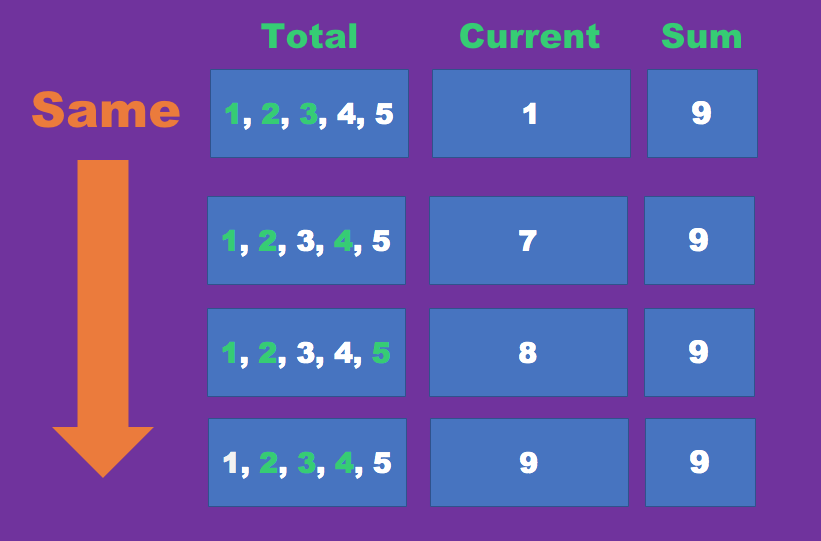
1, 2, 3 까지의 부서팀의 예산 금액에 허용되며 그 이상의 부서는 예산이 초과되는 관계로 무시를 한다.

경우의 수에 따른 각 부서팀의 예산을 합계하면 제한 금액에 들어오지만,

결국 부서팀의 갯수는 3인 관계로 같다.

즉, 각 부서의 예산을 정렬하여 첫 예산 종합의 경우의 수만 구해도

최대 몇 개의 부서만 허용되는지 쉽게 풀 수 있다.

모범답안

function solution(d, budget) {
    d.sort((a, b) => a - b);

    while (d.reduce((a, b) => (a + b), 0) > budget) d.pop();

    return d.length;
}

코드 메커니즘을 해석하자면

while 조건문에 reduce 메서드를 계산하여 budget보다 클 경우 pop 메서드를

통해 순차적으로 요소 하나씩 제거하여 탈출 조건이 성립되면 최종적으로 예산 부서팀 갯수가 도출된다.