지난 시간에 물리적 메모리 관리 기법으로 contiguous allocation에 대해 배웠다. 이 방법에서는 물리적인 메모리에 프로그램을 통째로 올려놓기 때문에 물리적인 주소로 주소변환하는 게 편하다. base register와 limit register를 이용해서 아주 간단하게 주소변환을 한다.
지금부터는 Noncontiguous Allocation 에 대해 알아보자.
Paging
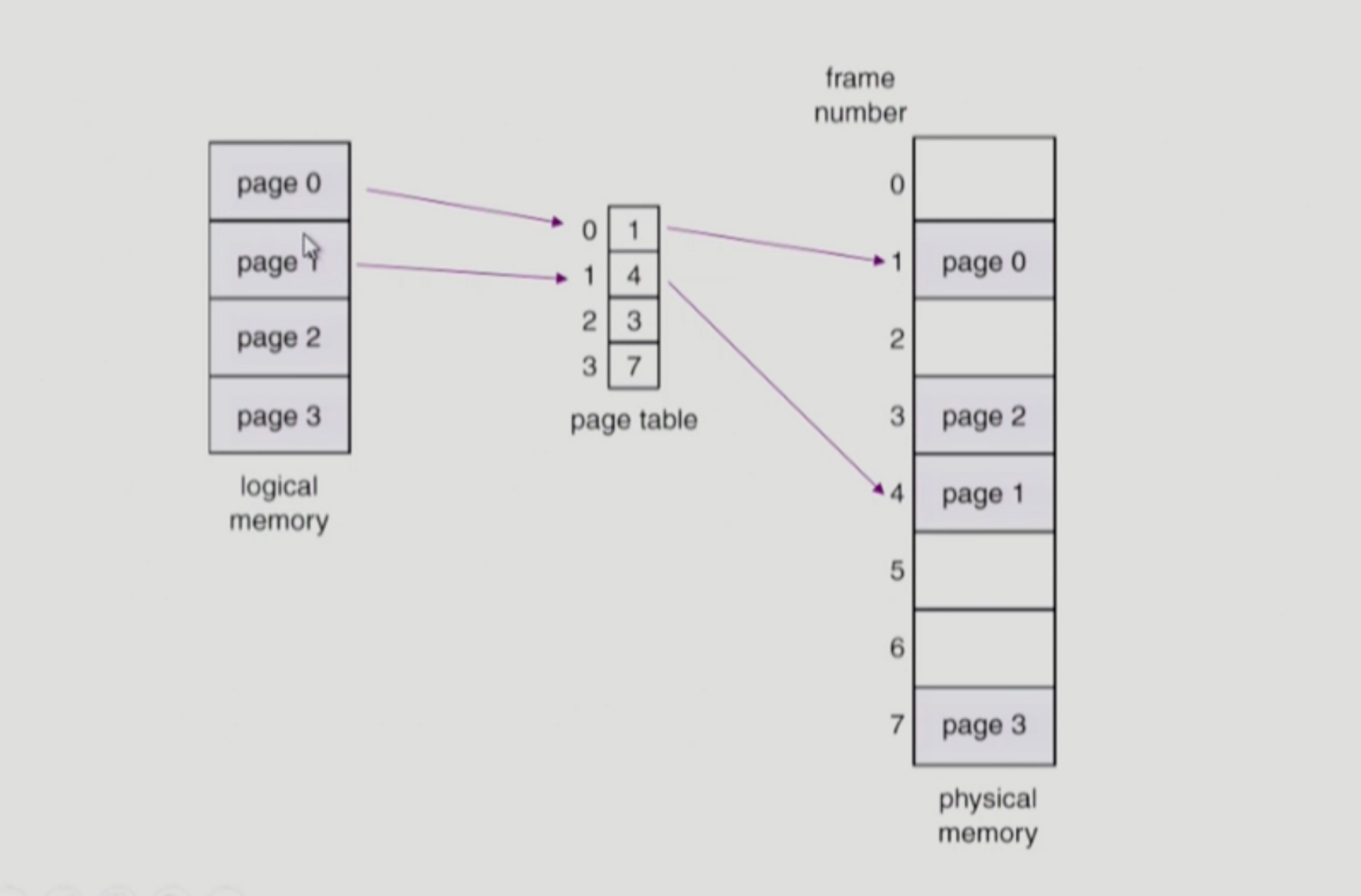
페이징 기법은 noncontiguous allocation 방법으로, 프로그램을 구성하는 주소공간이 일정한 크기의 페이지로 잘라져서 각 페이지가 필요에 따라 물리적 메모리의 비어있는 어느 위치든지 올라갈 수 있다.
이런 경우에는 주소변환이 단순하게 시작 위치만 가지고 일어날 수 있는 것이 아니고, 페이지별로 주소변환을 해주는 것이 필요하다. 따라서 주소변환 방법 역시 더 복잡해진다.
이 주소변환을 위해 page table을 사용한다. 이 page table은 각각의 논리적 페이지들이 물리적 메모리 어디에 올라가 있는지 나타낸다. page table은 논리적 메모리의 페이지 개수만큼의 엔트리가 존재하게 된다. (엔트리는 테이블에서 흔히 사용하는 용어이다.) 각 테이블의 엔트리에는 해당 인덱스에 대응하는 논리적 페이지가 몇번 물리적 frame에 올라가 있는지 저장되어 있다. 따라서 순차적으로 검색할 필요가 없고 인덱스를 이용해서 곧바로 접근할 수 있다.
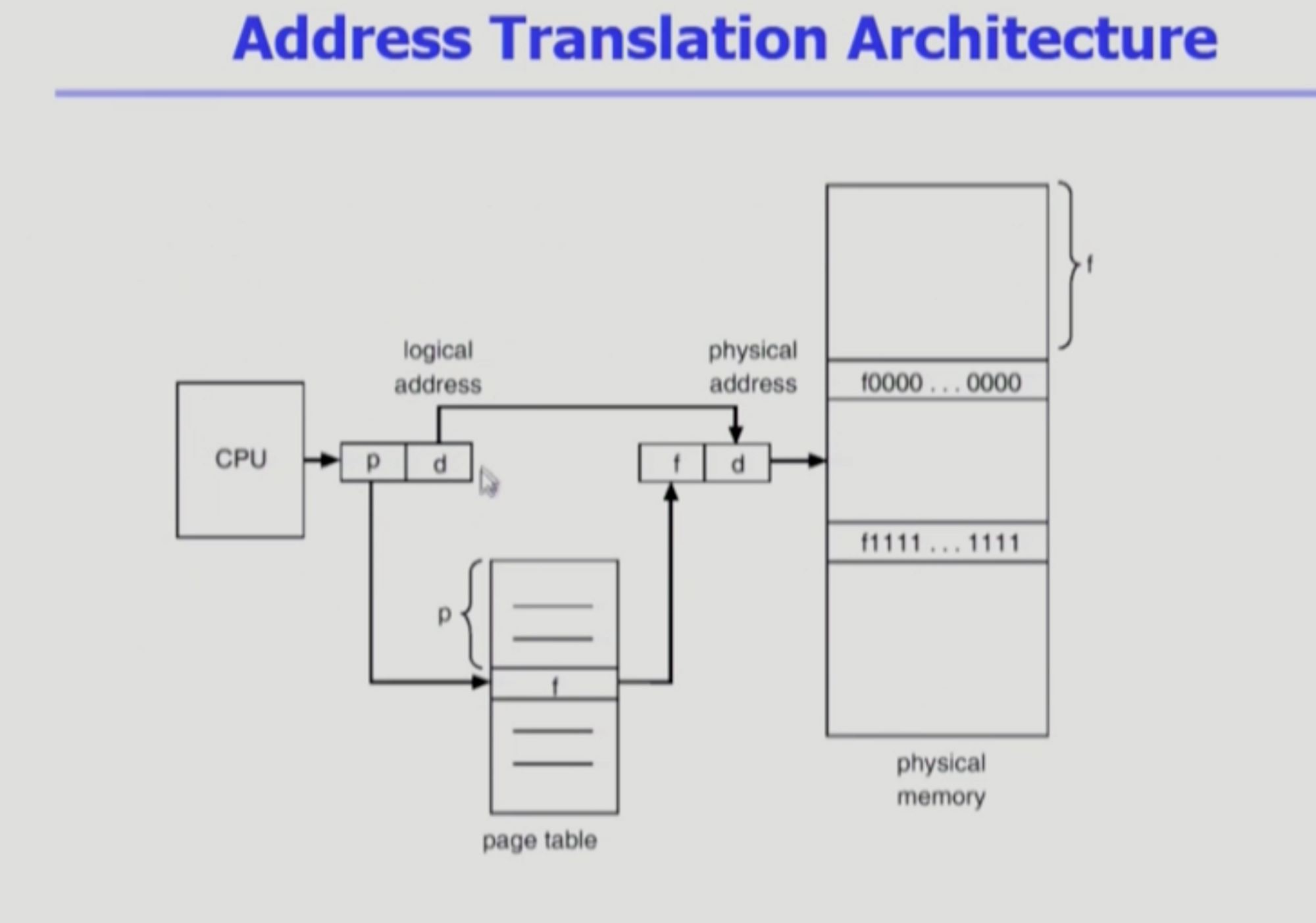
- p : 페이지 번호
- d : 페이지 내에서 얼만큼 떨어져 있는지 나타내는 offset
- f : page frame 번호
CPU가 논리적인 주소를 주면 주소변환을 위해 page table에 p만큼 떨어져 있는 f를 찾는다.
페이지 내에서 상대적인 위치는 똑같기 때문에 d는 바뀌지 않는다.
그렇다면 페이지 테이블이 어디에 들어가야 할까?
기본적인 MMU 기법에서는 레지스터, 즉 cpu 내의 아주 빠른 장치로 작업했다.
그런데 페이지 기법을 사용을 하면, 프로그램을 구성하는 주소공간을 페이지 단위로 자르는데 보통 이 페이지 크기가 4KB이다. 그렇기 때문에 주소공간의 크기가 매우 커지면 페이지 개수도 매우 많아지며 page table도 커진다. 또 프로그램마다 페이지 테이블이 별도로 저장되어야 한다. 그렇기 때문에 레지스터에도 집어넣을 수 없고, 메모리를 위한 주소변환이기 때문에 하드디스크에도 집어넣을 수 없다. 또한 캐시메모리에 들어가기에도 용량이 크다.
따라서 이를 메모리에 집어넣는다. 실제로 메모리에 접근하기 위해서는 주소변환을 해야 하는데 주소변환을 하려면 페이지 테이블이 필요하고, 페이지테이블이 또 메모리에 존재하기 때문에 메모리를 접근하기 위해서는 2번의 메모리 access가 필요하다. page table을 통한 주소변환을 위한 메모리접근이 필요하고, 주소변환이 되면 메모리에서 데이터를 접근하기 위해서 또 메모리 접근이 필요하다. 그렇기 때문에 시간이 많이 걸려 비용이 크다.
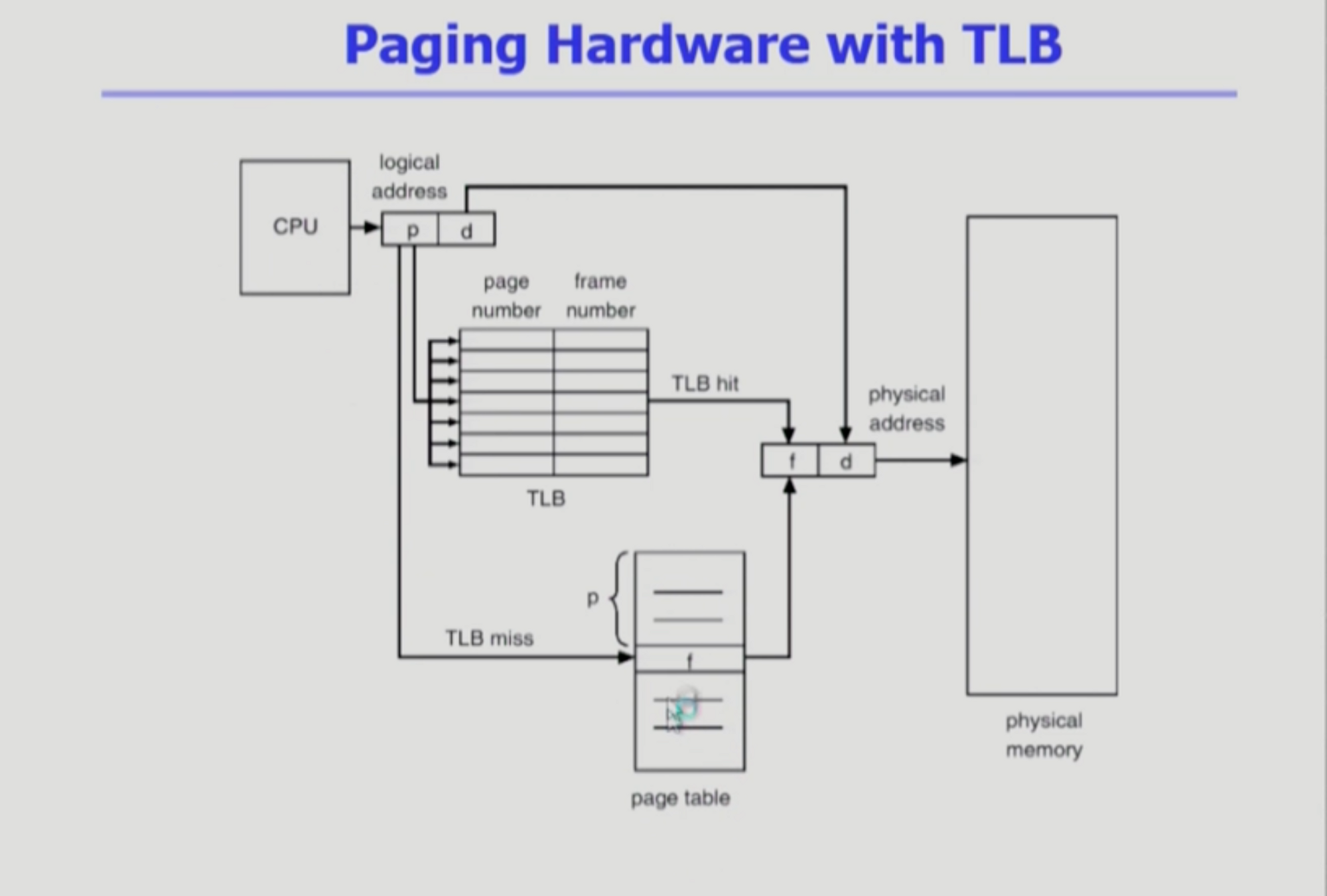
그래서 속도 향상을 위해 associative register로 구성되는 translation look-aside buffer(TLB)라는 별도의 하드웨어를 사용한다.
이는 일종의 캐시이다. 이것은 메인메모리보다 빠른, 메인메모리와 CPU 사이에 존재하는 주소변환을 해주는 계층이다. 주소변환을 위한 별도의 캐시가 TLB인 것이다.(데이터를 저장하는 캐시메모리와는 다르며 주소변환을 위한 것이다.) 메인메모리보다 접근속도가 빠르며 빈번히 등장하는 페이지에 대한 정보를 가지고 있다.
전체를 가지고 있는 것이 아니기 때문에 page number 와 frame number 모두를 쌍으로 가지고 있어야 한다. 또한 TLB전체 search를 해야 한다. 전체 search로 인한 성능 저하 방지를 위해 Parallel search가 가능한 associative register를 이용해 구현한다.
cpu가 주소공간 p를 주면 Parallel search를 한다. cpu가 논리적인 주소공간을 주면 TLB를 먼저 검색해서 TLB에 있는 정보로 주소변환이 가능한지 먼저 살펴본다. tlb에 없는 경우에는 page table을 통해 일반적인 주소변환을 하여 2번의 메모리 접근을 한다. 페이지 테이블이 각각의 프로세스마다 존재하기 때문에 tlb에 있는 정보도 프로세스마다 다르다. tlb에 있는 정보는 context switch가 발생할 때 flush를 시켜 모든 엔트리를 비워주어야 한다.
dynamic relocation 에서의 relocation register와 limit register가 페이징 기법에서는 어떻게 사용될까. page-table base register(PTBR)과 page-table length register(PTLR)로 사용된다. 메모리 상에 페이지 테이블이 어디에 있는지 시작 위치를 PTBR이 가지고 있고 페이지 테이블의 길이를 PTLR이 가지고 있다.

그럼 실제로 메모리에 접근하는 시간은 어떻게 될까. 보통은 tlb에 접근하는 시간을 입실론이라고 한다면, 이는 메인 메모리 접근하는 시간인 1보다 훨씬 작다. tlb 로부터 주소 변환이 찾아지는 비율을 알파라고 하면 그 시간은 2 + 입실론 - 알파와 같다. (1+엡실론 : 실제 메모리 접근 시간+tlb 접근 시간 / 2+엡실론 : (페이지테이블접근시간+실제메모리접근시간)+tlb접근시간) 실제로는 알파가 매우 크기 때문에 tlb를 사용하지 않을 때 접근 시간인 2보다 훨씬 작아진다.
Two-Level Page Table
이는 두 단계로 존재하는 페이지 테이블이다.
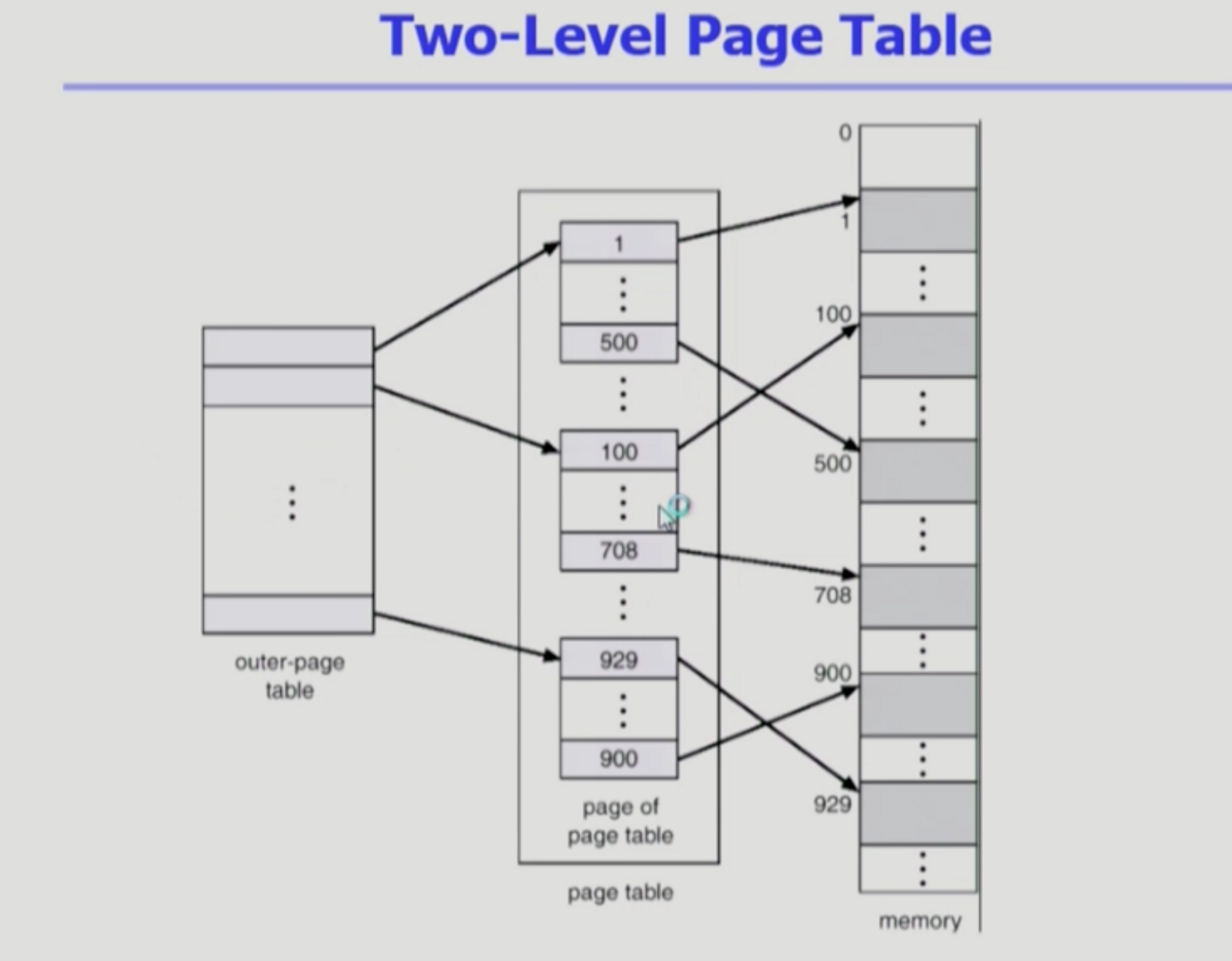
cpu가 논리적 주소를 주면 두 단계 페이지 테이블을 거쳐 메모리에 접근한다. (outer-page table → page table)
페이지 테이블 접근을 두번하기 때문에 속도는 줄어들지 않는다. 그러나 페이지 테이블을 위한 공간이 줄어든다. 이것이 two-level page table을 사용하는 목적이다.
address가 32비트로 구성되고, 최근에는 64비트도 사용한다. 32비트로 표현할 수 있는 전체 논리적인 주소가 몇개일까. 논리적인 주소가 32비트로 구성되면, 2^32개이며 0번지부터 2^32-1번지까지 주소공간을 매길 수 있다(메모리는 바이트 단위로 구분되므로 2^32byte를 구분할 수 있다). 즉, virtual memory 의 크기는 시스템이 사용하는 주소체계의 비트 수에 따라 달라진다.
(2^10 = K, 2^20 = M, 2^30 = G)
따라서 각 프로그램이 가질 수 있는 메모리의 크기는 4GB가 된다. 각 페이지 크기는 4KB. 총 4GB의 공간을 4KB로 쪼개면 페이지가 1M가 생긴다. 페이지 테이블의 엔트리도 1M개 필요하다.
또한 전체 메모리 주소공간 4GB 중에 프로그램의 주소공간(코드, 데이터, 스택)이 차지하는 부분을 극히 일부이다. 프로그램에 따라 좀 다르지만 대개 전체 공간 중에 상당히 일부분만 사용된다. 하지만 페이지 테이블은 인덱스로 접근되기 때문에 메모리에 비어있는 부분이 있다하더라도 페이지 테이블에서 빼버릴 수 없다.
이런 페이지 테이블을 다 메모리에 집어넣으면 공간 낭비가 심하다. 그렇기 때문에 2단계 페이지 테이블을 사용한다.

(마치 서울 안에 강남구 있듯이 p1 , p2가 존재)
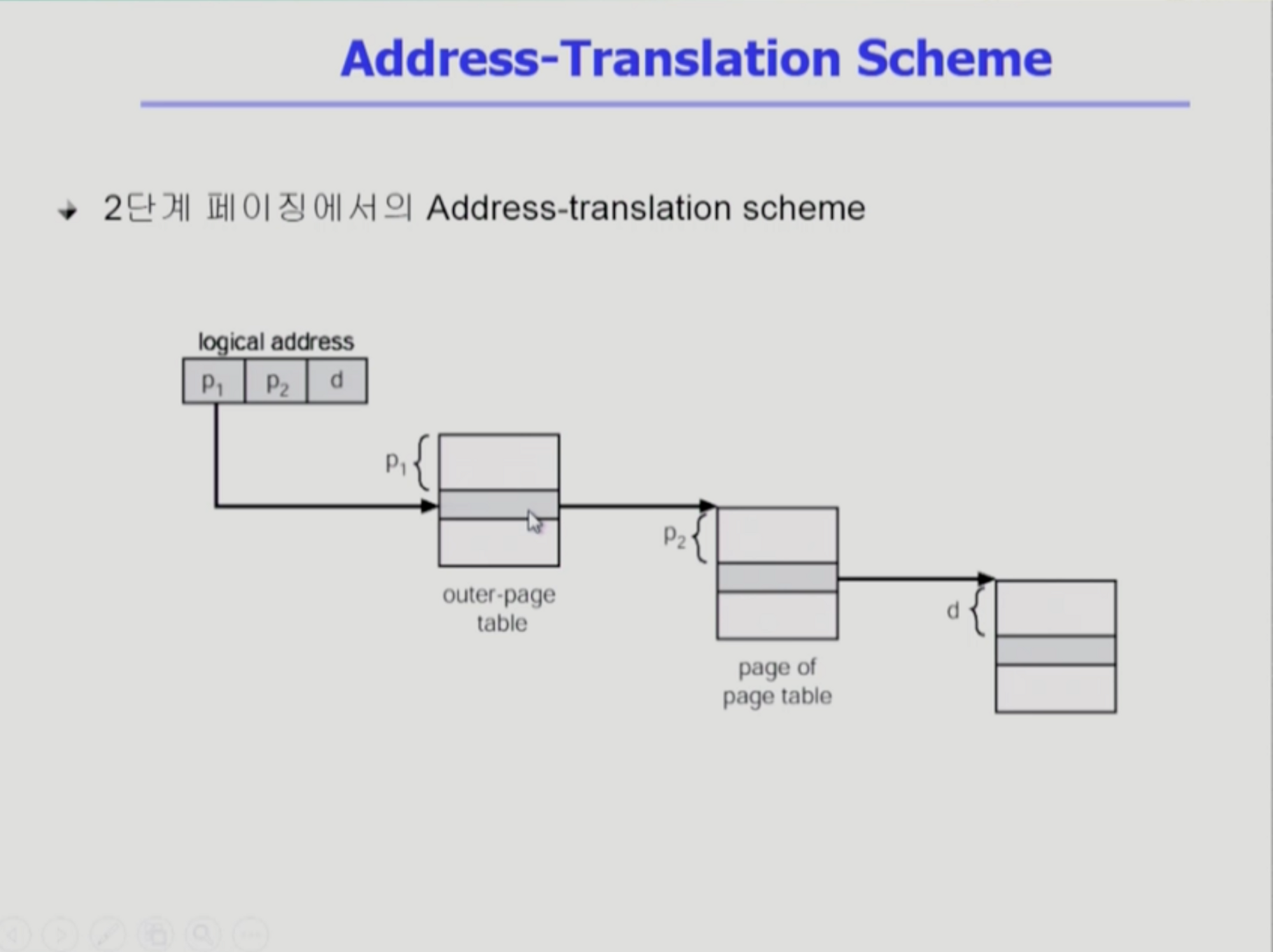
outer-page table 하나 당 안쪽 페이지 테이블들이 만들어진다. p1은 어떤 안쪽 페이지 테이블인지 가리키고 p2는 물리적인 페이지 frame 번호를 가리킨다. 페이지 프레임에서 d번째 떨어진 위치에서 원하는 정보를 찾을 수 있다.
이런식으로 이단계로 주소변환을 한다.
여기서 주의해야 할 점은 안쪽 페이지 테이블 각각의 크기는 페이지 크기와 같다. 즉 4KB이다. 안쪽 페이지 테이블 각각에 1K개 페이지를 집어넣을 수 있다. (페이지 하나가 4byte)

페이지 하나의 크기가 4KB이기 때문에 4KB안에서 주소구분을 하려면 (2^12byte) 12bit가 필요하다. 그래서 page offset은 12bit를 차지하고, P2는 위에서부터 몇번째 엔트리인지 구분해준다. 안쪽 테이블 안에 엔트리가 1K(2^10)개 있기 때문에 이를 구분하기 위해 P2는 10bit가 필요하다. 전체 32비트에서 32-10-12하면 바깥 테이블을 위한 페이지번호는 10비트가 된다.
이를 바꾸어 64비트 주소체제를 사용한다 생각해보자. 페이지 테이블은 똑같이 4KB이고 2단계 페이지테이블을 사용한다면? p1, p2, d는 몇비트가 필요할까?
앞서 말했듯 프로그램을 구성하는 공간 중 상당 부분이 사용 되지 않는다. 그런데 인덱스로 접근하기 때문에 사용되지 않는 공간에 대한 엔트리를 만들지 않을 수 없다. 그런데 이단계 페이지 테이블을 쓰면 그것을 해소할 수 있다.
바깥쪽 테이블은 전체 논리적 테이블 크기만큼 만들어지지만, 사용되지 않는 메모리 영역은 NULL이 되어있고 사용되는 것만 안쪽 테이블을 가리킨다. 즉, 사용되지 않는 부분에 대해서는 안쪽 테이블이 만들어지지 않는다. 따라서 공간을 효율적으로 사용할 수 있는 것이다.
