*본 게시글은 유튜브 '김성범[ 교수 / 산업경영공학부 ]' [ 핵심 머신러닝 ]뉴럴네트워크모델 1 (구조, 비용함수, 경사하강법) 자료를 참고한 점임을 알립니다.
Neural Network
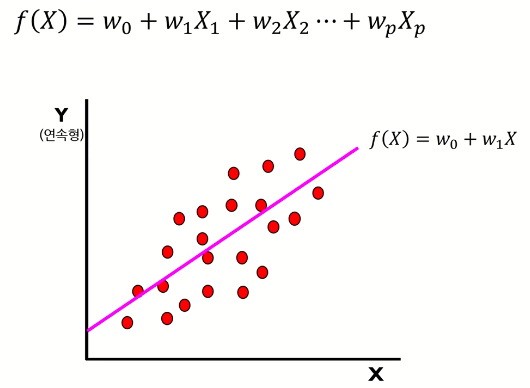
1. 선형 회귀 모델
- 입력변수(x)의 선형 결합을 통해 출력변수(y)를 표현
- 출력변수(y)는 실수의 범위 내에서 연속적인 값 => '연속형'
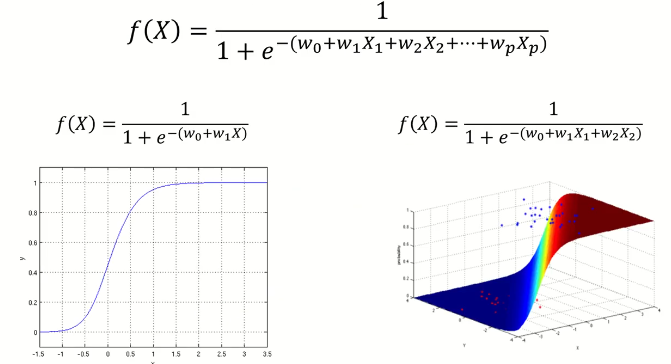
2. 로지스틱 회귀모델
-
입력변수(x)의 선형 결합값을 로지스틱 함수에 입력하여 비선형 결합(σ)을 통해 출력변수(y)를 표현
-
출력변수(y)는 특정 범주 및 카테고리 중 하나의 값 => '범주형'
-
이진 범주형 : 0 또는 1 (True or False)
-
다중 범주형 : 맑음 또는 흐림 또는 비 또는 눈
-
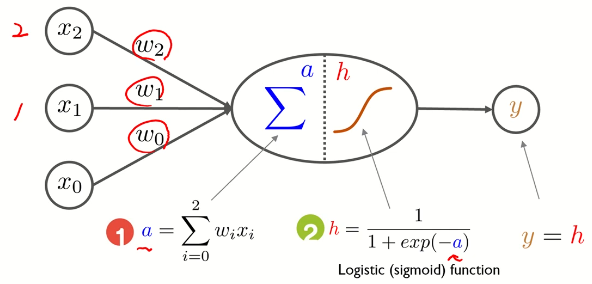
그림으로 표현
3. 다중 퍼셉트론(Multi-Layer Perceptron)
- 입력층 : 입력변수의 수 = 입력노드의 수
- 은닉층
- 출력층 : 출력노드의 수 = 출력변수의 범주 개수(범주형), 출력 변수의 갯수(연속형)
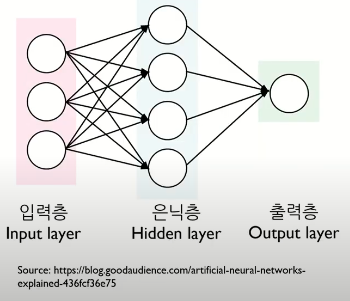
- MLP(Multi-Layer Perceptron) == ANN(Artifical Nerural Networks)
4. 선형 회귀 / 로지스틱 회귀 / 뉴럴 네트워크 비교
-
선형 회귀 모델
f(x)=w0+w1X1+w2X2
-
로지스틱 회귀 모델
f(x)=1+e−(w0+w1X1+w2X2)1
-
뉴럴 네트워크
f(x)=1+e−(z01+z11(1+e−(w01+w11X1+w21X2)1)+z21(1+e−(w02+w12X1+w22X2)1))1
5. 활성화 함수(Activation Function)

6. 비용 함수(Cost Function)
- MSE
L=n1i=1∑n(yi−y^i)2
- CrossEntropy
L=−i∑tilogpi ex) 3 Classes에 대해 계산
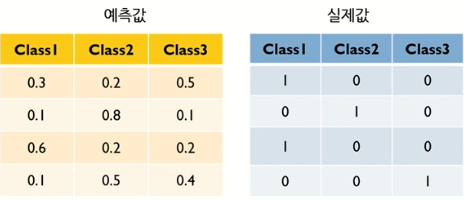
−i=1∑4tilogpi=−[ln(0.3)+ln(0.8)+ln(0.6)+ln(0.4)]=2.85
∗CrossEntropy값을낮추는wegiht,bias을탐색하는과정이Training과정
7. 경사하강법 (Gradient Descent)
- Gradient Descent Method: First-Order Optimization Algorithm
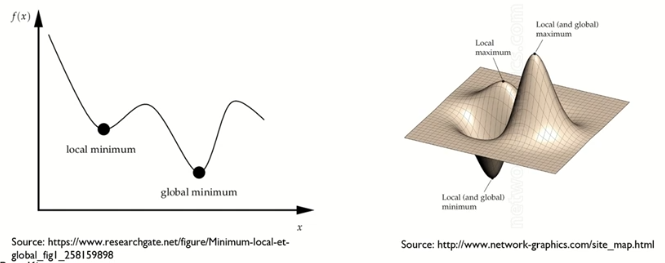
- Optimization : 함수의 최솟값 혹은 최댓값을 찾는 과정
- Turning Points의 개수는 함수의 차수에 의해 결정
- 모든 Turning Point가 최솟값 혹은 최댓값은 아님
- 전역 최솟값(Global Minimum) : 최솟값들 중 가장 작은 최솟값
- 지역 최솟값(Local Minimum) : 지역적인 최솟값
-
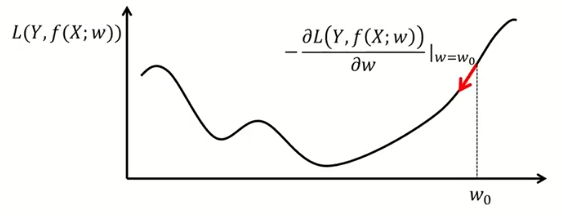
경사하강법(Gradient Descent Method)
-
비용함수를 최소화하는 weight들을 찾고자할 때 활용하는 방법론
-
gradient가 줄어드는 방향으로 weight들을 찾다보면 최솟값을 찾을 수 있음
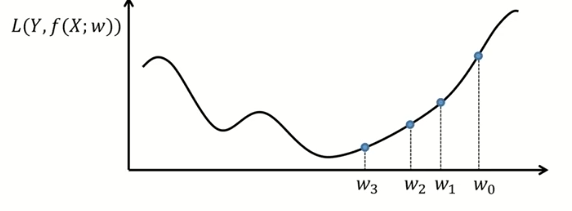
wτ+1=wτ−α⋅L′(wτ)
(wτ+1:이전weight,wτ:현재weight,learningrate:학습률(0<α<1))
-
wτ에 따라 wτ+1가 증가 혹은 감소
참고 자료










